Calculer avec Maple

• Calculs avec des nombres :
  • Evaluation numérique :

    >?evalf 
    >?normal
    > evalf(32!/271);  evalf(Pi,150); fnormal(32!/271); evalc(2^(1+I));

    

    Correction:

    • Le nombre de chiffres donné comme deuxième argument de evalf n'est pas le nombre de chiffres significatifs, mais le nombre de chiffres avec lesquels le calcul est effectué. On ne connaît donc pas a priori le nombre de chiffres significatifs du résultat.
      
    • La fonction evalf, comme un certain nombre de fonctions Maple, garde en mémoire les valeurs calculées. Dans le cas de l'exercice, le calcul avec 50 chiffres est gardé en mémoire et est utilisé pour le dernier calcul avec 10 chiffres.

      > e:=exp(Pi*sqrt(163))-262537412640768744;
      > for i to 5 do
      >  evalf(e,10*i);
      > od;
      > evalf(e,10);

      > evalf(Pi,10000);
      > evalf(Pi,10001);

      >  e:=300! ;
      > ifactor(e)

  • calcul de pgcd et ppcm.

    

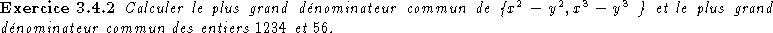
    Correction:

    > gcd(x^2-y^2,x^3-y^3);
    > igcdex(1234,56,'s','t');

  • division entière: ex : 1/2345 mod 6;
  • nombres algébriques : un nombre algébrique est une racine d'un polynôme à coefficients rationnels. Il est souvent impossible d'obtenir une expression symbolique de ces nombres, mais on peut avoir envie de poursuivre des calculs avec des nombres algébriques en se rappellant juste de quel polynôme ils sont racine. La fonction RootOf sert à cela. Par exemple on peut utiliser alpha:=RootOf(z^7+z^5-2,z); pour désigner les racines du polynôme z^7+z^5-2,z ( voir aussi allvalues(alpha); ).

    > convert((-8)^(1/3),RootOf); convert(",radical);

  • nombres complexes: z:=a+I*b; Re(z); Im(z);. calcul de résidu:

    > readlib(residue): f:=exp(a*z)/(1+exp(z)); residue(f,z=Pi*I);