Résolution de systèmes linéaires

  

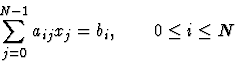
La méthode de Gauss transforme un système linéaire en un système triangulaire équivalent. L'idée est de résoudre la première équation en x₀, puis d'éliminer x₀ des équations suivantes, ensuite de résoudre la seconde équation en x₁, puis d'éliminer x₁ des équations suivantes, et ainsi de suite. Initialement, on a le système de N équations à N inconnues :

$$\sum_{j=0}^{N-1} a_{ij} x_j = b_i, \qquad 0 \le i\le N$$

Les fonctions implémentant cet algorithme vont opérer sur les tableaux globaux :

     

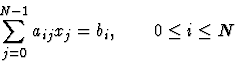
#define N 10
double a[N][N];   /* la matrice */
double b[N];      /* le membre droit */
double x[N];      /* la solution */

La première ligne, << # define N 10 >>, est une directive de (macro-)définition du préprocesseur ; celui-ci substituera << 10 >> à << N >> dans toutes les lignes suivantes du programme avant que le programme ne soit compilé. Une telle directive a dans ce cas précis l'intérêt de paramétrer la taille des tableaux, ce qui ne serait pas possible si N était une variable, même spécifiée const.

Pour décrire l'algorithme, on posera a_ij⁰ = a_ij et b_i⁰ = b_i. Après k itérations, on obtient le système :

$$\begin{array} {ccccccccccccc} a_{00}^k x_0 &+ &a_{01}^k x_1 ... ...&\ldots &+ &a_{N-1,N-1}^k x_{N-1} & = &b_{N-1}^k \\ \end{array}$$

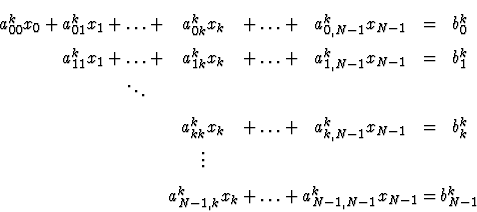
Les k premières équations ne seront plus modifiées. Il faut maintenant éliminer x_k. On n'utilise pas nécessairement l'équation $a_{kk}^k x_k + \ldots$ car il se peut que le coefficient a_kk^k soit nul ; on va donc chercher un indice l, avec $k\le l\le N-1$, tel que a_lk^k ait la plus grande valeur absolue (pour minimiser les problèmes d'arrondi) :

int pivot(int k) {
  /* cherche l'indice d'un pivot dans k..N-1 */
  int i;
  int l = k;
  double max = fabs(a[k][k]);

  for (i=k+1; i<N; i++) {
    if (fabs(a[i][k]) > max) {
      l = i;
      max = fabs(a[i][k]);
    }
  }
  printf("pivot(%d) = %d\n", k, l);
  return l;
}

Si la valeur du pivot est non nulle, on échange les équations $a_{kk}^k x_k + \ldots$ et $a_{lk}^k x_k + \ldots$ :

void echanger(int k, int l) {
  /* échange les lignes k et l du système
     à partir de la colonne k */
  double temp;
  int j;

  for (j=k; j<N; j++) {
    temp = a[k][j];
    a[k][j] = a[l][j];
    a[l][j] = temp;
  }
  temp = b[k];
  b[k] = b[l];
  b[l] = temp;
}

Après cet échange, les k+1 premières équations ne seront plus modifiées. On a donc désormais $a_{kk}^k \not= 0$. On peut donc éliminer x_k de la ligne i ($k+1\le i \le N-1$) en ajoutant cette ligne à -a_ik^k/a_kk^k fois la ligne k : on obtient ainsi les coefficients du système à l'issue de cette k+1-ème itération, par << pivotage >> :

$$\begin{array} {rcll} a_{ij}^{k+1} &= &a_{ij}^k - a_{ik}^k a_... ..._{ik}^k b_{k}^k / a_{kk}^k, &\quad k+1\le i \le N-1\end{array}$$

Ceci se transcrit en la procédure pivoter :

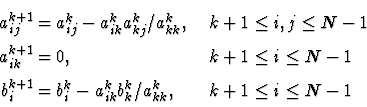
void pivoter(int k) {
  /* élimine x_k des lignes k+1..N-1 */
  int i,j;

  for (i=k+1; i<N; i++) {
    double q = a[i][k]/a[k][k];

    b[i] = b[i] - q * b[k];
    for (j=k+1; j<N; j++) {
      a[i][j] = a[i][j] - q * a[k][j];
    }
  }
}

Si, à l'une des itérations, la valeur du pivot est nulle, c'est que le système n'est pas régulier, et la résolution s'arrête (c'est le rôle du break   dans la fonction gauss). Si le système est régulier (c'est-à-dire de rang N), il est transformé en un système triangulaire en N-1 itérations.

int gauss() {

  /* si le système "a x = b" est régulier, le transforme en un 
     système triangulaire en N-1 itérations et retourne 1, 
     sinon retourne 0 */

  int k, l;
  int inversible;

  for (k=0; k<N-1; k++) {
    l = pivot(k);
    inversible = (fabs(a[l][k]) > DBL_EPSILON);
    if (inversible) {
      if (l > k) {
        echanger(k,l);
      }
      pivoter(k);
    } else break;
  }
  return inversible;
}

Il reste à résoudre un système triangulaire supérieur :

int systeme_triangulaire() {

/* calcule la solution x d'un système triangulaire supérieur 
   "a x = b" et retourne 1 s'il est régulier, 
    et retourne 0 sinon */

  int i, j;
  double v;

  for (i=N-1; i>=0; i--) {
    if (fabs(a[i][i])<EPS) {
      return 0;
    } else {
      v = b[i];
      for (j=i+1; j<N; j++) {
        v = v - a[i][j]*x[j];
      }
      x[i] = v/a[i][i];
    }
  }
  return 1;
}

La complexité de cet algorithme est en $\Theta(N^3)$.