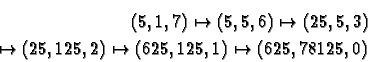Un exemple : l'exponentiation

Java ne disposant pas d'un opérateur d'exponentiation entière, il faut programmer cette opération (dans le cas des nombres flottants, utiliser Math.exp()). Le programme suivant calcule x^e, pour des entiers x et e avec $e\ge 0$, en accumulant (par multiplication) xdans y, ceci e fois, l'expression y*x^e étant un invariant de boucle :  

  static int exp(int x, int e) {
    int y = 1;
    while (e != 0) {
      y = y*x;
      e = e-1;
    }
    return y;
  }

Chaque itération effectue une transformation $(y,e)\mapsto(y',e')$ ; par exemple, le calcul de exp(5,8) effectue les transformations successives suivantes de (y,e) :

$$\begin{eqnarray*}(1,8) \mapsto (5,7) \mapsto (25,6) \mapsto (125,5) \mapsto (625... ... (3125,3) \mapsto (15625,2) \mapsto (78125,1) \mapsto (390625,0) \end{eqnarray*}$$

On vérifie l'invariant

y' x^e' = yxx^e-1 = y x^e

On a donc l'égalité de valeur de cet invariant au début de la boucle (quand y=1) et à la fin de la boucle (quand e=0) :

x^e_initial = y_final

On notera que la version récursive équivalente à ce programme itératif n'est pas celle que l'on écrirait directement à partir de la définition par récurrence de la fonction puissance, mais est la suivante (la boucle du while modifiant les variables y et e, la fonction récursive doit prendre ces valeurs en argument) :

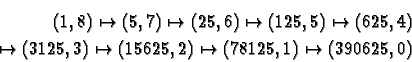
  private static int exp_aux(int x, int y, int e) {
    if (e == 0) {
      return y;
    } else {
      return exp_aux(x, y*x, e-1);
    }
  }
  
  static int exp(int x, int e) {
    return exp_aux(x,1,e);
  }

La fonction exp_aux est une fonction auxiliaire qui ne sera appelée que par exp ; c'est pourquoi elle est déclarée private.

Pour les trois programmes précédents, le nombre d'itérations ou d'appels récursifs est l'entier e. Il est possible d'accélérer significativement ce calcul en ramenant ce nombre de e à au plus $2\log_2 e$, grâce à la propriété suivante :

$$\begin{eqnarray*}x^{2e+1} &= &x * x^{2e} \\ x^{2e} &= &(x^2)^e \end{eqnarray*}$$

Par exemple, x¹⁰ = (x²)⁵ = x² (x²)⁴ = x² ((x²)²)² en quatre multiplications au lieu de 9. On obtient ainsi la définition    

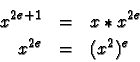
  private static int exp_fastrec_aux(int x, int y, int e) {
    if (e == 0) {
      return y;
    } else if (e % 2 == 1) {
      return exp_fastrec_aux(x, x*y, e-1);
    } else {
      return exp_fastrec_aux(x*x, y, e/2);
    }
  }

La version itérative s'écrit facilement à partir de cette version récursive terminale, en remplaçant la liste des arguments des appels récursifs par des affectations appropriées :

  static int exp_fastiter(int x, int e) {
    int y = 1;
    while (e!=0) {
      if (e%2 == 1) {
        y = x*y;
        e = e-1;
      } else {
        x = x*x;
        e = e/2;
      }
    }
    return y;
  }

Le cas bénéficiant de la plus forte accélération est celui où l'exposant est une puissance de 2 ; voici la suite des transformations de (x,y,e)pour le calcul de 5⁸ (en trois itérations au lieu de 8):

$$(5,1,8) \mapsto (25,1,4) \mapsto (625,1,2) \mapsto (390625,1,0)$$

La situation est moins favorable quand l'exposant n'est pas une puissance de 2 ; le calcul de 5⁷ se fait en 5 itérations, soit moins de $2\log_2 7$ :

$$\begin{eqnarray*}(5,1,7) \mapsto (5,5,6) \mapsto (25,5,3) \\ \mapsto (25,125,2) \mapsto (625,125,1) \mapsto (625,78125,0) \end{eqnarray*}$$

Cet algorithme est décrit dans le Chandah Sutra d'Acharya Pingala (écrit avant 200 ans avant J.C.).