1. Si 1 est valeur propre de Q, 1 est aussi valeur propre de ^tQ, mais dans ce cas, si u est un vecteur propre de ^tQ,

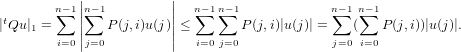
| | n∑−1||n∑−1 || n∑−1n∑−1 n−∑ 1n∑−1 |tQu |1 = || P(j,i)u(j)||≤ P (j,i)|u(j)| = ( P (j,i))|u(j)|. i=0|j=0 | i=0 j=0 j=0 i=0

Comme ∑ _i=0ⁿ⁻¹P(j,i) = 1 pour j = 0,…,n− 2 (car P(j,n) = 0) et ∑ _i=0ⁿ⁻¹P(n− 1,i) = 1 −P(n− 1,n) < 1, on a |^tPu|₁ < |u|₁. Ce qui interdit à 1 d’être valeur propre de ^tP donc de P.