On prendra pour ![]() (on cherche donc à approximer
(on cherche donc à approximer
![]() ).
).
Implémenter cet algorithme et étudier la convergence pour
![]() ,
, ![]() et
et ![]() ,
, ![]() .
.
Dans le cas ![]() , tester les valeurs
, tester les valeurs ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Commenter les difficultés que l'on peut rencontrer.
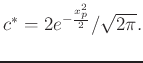 Pour quelle valeur de
Pour quelle valeur de Verifier le théorème de la limite centrale pour cet algorithme sous cette condition.
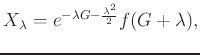 mais
mais
On prendra ![]() .
.
Pour cela, on pose ![]() , puis
, puis
Implémenter cet algorithme en ramenant ![]() à
à ![]() si
si ![]() dépasse la
valeur de
dépasse la
valeur de ![]() (procédure dite de ``projection de Chen''). Vérifier que
l'algorithme converge (mieux!).
(procédure dite de ``projection de Chen''). Vérifier que
l'algorithme converge (mieux!).