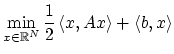Algorithmes de gradient à pas fixe
suite

J.Ph. Chancelier¹

Le but de cette première séance est double, se refamiliariser avec la programmation en Scilab, commencer à voir la mise en oeuvre d'algorithmes d'optimisation.

1 Minimisation de fonctionnelles quadratique

On cherche ici à programmer un algorithme de gradient à pas constant pour un problème quadratique :

$\displaystyle \min_{x \in \mathbb{R}^{N}} \frac{1}{2} \left< x, Ax \right> + \left< b, x \right>$

(1)

Écrire une première fonction qui tire de façon aléatoire un matrice N x N définie positive dont on peut contrôler la plus petite valeur propre (assurer qu'elle est plus grande qu'une valeur donnée) (rand, diag, inv)

 
function A=defpos(n,lmin,lmax)
  // tirage aléatoire d'une matrice définie positive
  // dont le spectre aléatoire est réel uniforme sur [lmin,lmax]
  A=diag( (lmax-lmin)*rand(N,1)+lmin);
  P=rand(N,N);
  A=P*A*inv(P);
endfunction
                                                                                 
function A=defpos_sym(n,lmin,lmax)
  // tirage aléatoire d'une matrice définie positive et symetrique
  // dont le spectre aléatoire est réel uniforme sur [lmin,lmax]
  A=diag((lmax-lmin)*rand(N,1)+lmin);
  [U,H]=hess(rand(N,N));
  A=U*A*U';
endfunction

A=defpos_sym(N,2,3);
b=rand(N,1);

Une remarque: génériquement une matrice aléatoire (ici avec loi uniforme) est inversible :

 
ne=100;
for i=1:ne
  A1=rand(N,N);
  if rank(A1)<>N then pause;
  end;
end

Écrire une fonction Scilab qui calcule le critère (1) et une fonction qui calcule le gradient du critère.

 
function y=f(x,A,b)
  y = (1/2)* x'*A*x  + b'*x
endfunction
 
function y=df(x,A,b)
  y = (A+A')*x/2  + b;
endfunction

Programmer un algorithme de gradient à pas constant sur le problème quadratique. Il faudra évaluer numériquement la borne maximale du pas de gradient et choisir un critère d'arrêt. On pourra aussi tracer au cours des itérations l'évolution de la fonction coût et évaluer les temps de calculs (timer)

 
function rho_max=rmax(A)
  alpha = min(abs(spec((A+A')/2)))
  // valeur de Lipschitz du gradient
  C= norm((A+A')/2,2)
  // contrainte sur le pas de gradient
  rho_max= 2*alpha/C^2
endfunction

 
function [c,xn,fxn]=gradient(x0,f,df,rho,stop,nmax,A,b)
  // a la fin de l'algoithme c contiendra les valeurs f(xi,...) 
  // xn et fxn sont les valeurs finales obtenues 
  // rho : pas de gradient 
  // stop : valeur numérique du critère d'arret 
  // nmax : nombre d'itérations maximales 
endfunction

Rendre le programme plus générique

 
function [c,xn,fxn]=gradient(x0,f,df,rho,stop,nmax,varargin)
  // a la fin de l'algoithme c contiendra les valeurs f(xi,...) 
  // xn et fxn sont les valeurs finales obtenues 
  // rho : pas de gradient 
  // stop : valeur numérique du critère d'arret 
  // nmax : nombre d'itérations maximales 
  .... f(x,varargin(:)).... 
endfunction

Calculer la solution du problème d'optimisation revient ici à résoudre un système linéaire. On pourra comparer la solution du problème d'optimisation avec la solution obtenue en utilisant des algorithmes de résolution de systèmes linéaires de Scilab.

1.1 Rajout d'une contrainte

On rajoute maintenant au problème d'optimisation une contrainte linéaire de la forme . Pour que l'ensemble admissible ne soit pas réduit à , il faut bien s'assurer que la matrice à un noyau de dimension non nulle.

Écrire une fonction qui tire de façon aléatoire un matrice N x N dont le rang est par exemple N/2 (indication : si M est une matrice n x m aléatoire quel est le rang générique de M*M' ? ).

Reprendre la première partie avec un nouveau critère d'optimisation ou on pénalise la contrainte en rajoutant au critère un terme $(1/(2\epsilon))* \Vert Tx\Vert$ :

$\displaystyle \min_{x \in \mathbb{R}^{N}} \frac{1}{2} \left< x, Ax \right> + \left< b, x \right> + \frac{1}{2\epsilon} \left< Tx, Tx \right>$

(2)

1.2 Un peu d'algèbre linéaire

En utilisant la fonction colcomp (compression de colonnes) On peut obtenir une base du noyau de l'opérateur . Cela permet d'écrire les vecteurs admissibles du problème avec contraintes sous la forme . On se ramène ainsi à un problème d'optimisation sans contraintes en . Le programmer et comparer avec la section précédente.

Que se passe-t-il si le rang de la matrice n'est pas égale au nombre de lignes de ? (c'est d'ailleurs ce qui se passe avec la méthode que nous avons utilisé pour obtenir T).

Se ramener à une structure de contrainte ou T est de rang plein (rowcomp).

Résoudre avec Scilab le système linéaire :

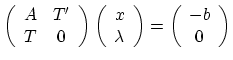$\displaystyle \left( \begin{array}{cc} A & T' T & 0 \end{array} \right) \lef... ...mbda \end{array} \right) = \left( \begin{array}{c} - b 0 \end{array} \right)$

(3)

2 Un problème de fil pesant (d'après Ciarlet, Joly. Ensta)

On se propose maintenant de trouver la position d'équilibre d'un fil pesant fixé à ses deux extrémités en résolvant un problème de minimisation. le fil pesant est caractérisé par son élévation . Il est fixé a la position à l'élévation et à la position à l'élévation . La longueur du fil est fixée . En minimisant l'énergie potentielle du fil on est conduit au problème de minimisation suivant :

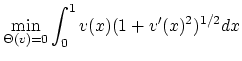$\displaystyle \min_{ \Theta(v)=0} \int_{0}^{1} v(x) (1+ v'(x)^2 )^{1/2} dx$

(4)

où les contraintes $\Theta(v)=0$ sont :

$\displaystyle v(0) -a$	$\displaystyle =$	0
$\displaystyle v(1) -b$	$\displaystyle =$	0
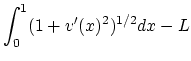$\displaystyle \int_{0}^{1} (1+v'(x)^2)^{1/2} dx - L$	$\displaystyle =$	0

Pour résoudre ce problème numériquement nous allons tout d'abord éliminer la contrainte portant sur la longueur de la corde par pénalisation. On va remplacer le problème initial par :

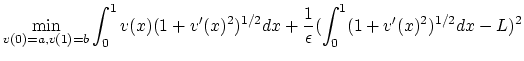$\displaystyle \min_{v(0)= a, v(1)=b} \int_{0}^{1} v(x) (1+ v'(x)^2 )^{1/2} dx + \frac{1}{\epsilon} ( \int_{0}^{1} (1+v'(x)^2)^{1/2} dx - L )^2$

(5)

Pour se ramener à un problème d'optimisation dans un espace de dimension finie, on va chercher sous la forme d'une fonction affine par morceaux. Soient $(x_i)_{i=0,N}$ des points régulièrement espacés sur , (). On cherche affine par morceaux sur les intervalles $[x_i,x_{i+1}]$ . Soit $(v_i)_{i=0,N}$ le vecteur des valeurs de au points , s'écrit :

$\displaystyle v_h(x) = v_i + (x-x_i)(v_{i+1}-v_i)$ sur $\displaystyle \quad [x_i,x_{i+1}]$

(6)

Le problème d'optimisation sur $\mathbb{R}^{N+1}$ s'écrit :

$\displaystyle \min_{ v_0 = a, v_N = b} J(v)$

(7)

avec

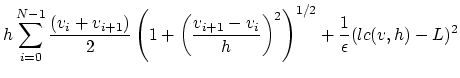$\displaystyle J(v)$	$\displaystyle =$	$\displaystyle h \sum_{i=0}^{N-1} \frac{(v_i+v_{i+1})}{2} \left( 1 + {\left(\frac{v_{i+1} -v_{i}}{h}\right)}^2 \right)^{1/2} + \frac{1}{\epsilon} (lc(v,h) -L)^2$
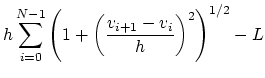$\displaystyle lc(v,h)$	$\displaystyle =$	$\displaystyle h \sum_{i=0}^{N-1}\left( 1 + {\left(\frac{v_{i+1} -v_{i}}{h}\right)}^2 \right)^{1/2} -L$

2.1 Un algorithme de gradient

Pour résoudre numériquement ce problème on va utiliser une méthode de gradient. On notera que les deux contraintes qui restent et ne seront pas traités comme des contraintes d'un problème d'optimisation. Ces deux valeurs de étant connues le problème d'optimisation se pose sur $\mathbb{R}^{N-1}$ .

L'algorithme est donc :

$\displaystyle v^{k+1} = v^k - \rho \Delta J(v^k)$

(8)

2.2 Résolution numérique avec Scilab

Comme on le voit sur l'équation (8) l'algorithme de gradient est un algorithme vectoriel, le vecteur est mis à jour à chaque itération. On devra tenir compte de ce fait et programmer l'algorithme de gradient de façon vectorielle en Scilab. La seule boucle for du programme sera la boucle d'itération (8).

On pourra au cours de l'algorithme d'optimisation tracer la position de la corde et voir ce tracé évoluer au cours de l'algorithme.

On pourra programmer les fonctions suivantes :

La fonction coût du problème pénalisé

function [j]=J(v,L,h,eps)
... 
endfunction

La fonction $( 1 + ((x-y)/h).^2)^{1/2}$ pour

vectoriels.

function [y]=R(v1,v2,h) 
... 
endfunction

La dérivée de par rapport à , à nouveau vectorielle.
```
function [y]=Dr(v1,v2,h)
...
endfunction
```
la longueur de la corde :
```
function [l]=lc(v,h) 
... 
endfunction
```

le gradient de

function [dj]= dJ(v,L,h,eps) 
... 
endfunction

`v(1:$-1)`	extraction d'un sous vecteur `$` désigne le dernier élément
`.*`	multiplication termes à termes
`.^`	exponentiation termes à termes
`sum`	somme des éléments d'un vecteur
`sqrt`	racine
`linspace`	points régulièrement espacés
`modulo`	fonction modulo
`plot2d`	tracé de courbes 2D

Notes

... Chancelier ¹: Cermics, École Nationale des Ponts et Chaussées, 6 et 8 avenue Blaise Pascal, 77455, Marne la Vallée, Cedex 2

Algorithmes de gradient à pas fixe suite