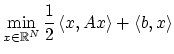Algorithmes de gradient à pas fixe
Éléments de réponse

J.Ph. Chancelier¹

Version pdf de ce document

On pourra se reporter au Cours d'optimisation de Guy Cohen pour les résultats en optimisation sous contrainte.

1 Minimisation de fonctionnelles quadratique

On cherche ici à programmer un algorithme de gradient à pas constant pour un problème quadratique :

$$\min_{x \in \mathbb{R}^{N}} \frac{1}{2} \left< x, Ax \right> + \left< b, x \right>$$ (1)

Écrire une première fonction qui tire de façon aléatoire un matrice N x N définie positive dont on peut contrôler la plus petite valeur propre (assurer qu'elle est plus grande qu'une valeur donnée) (rand, diag, inv)

On tire une matrice aléatoire diagonale avec une loi uniforme sur $(lmin,lmax)$ pour les éléments de la diagonale et on tire une matrice de changement de base aléatoire.

 
function A=defpos(n,lmin,lmax)
  A=diag( (lmax-lmin)*rand(N,1)+lmin);
  P=rand(N,N);
  A=P*A*inv(P);
endfunction

Écrire une première fonction qui tire de façon aléatoire un matrice N x N symétrique définie positive dont on peut contrôler la plus petite valeur propre (assurer qu'elle est plus grande qu'une valeur donnée) (rand, diag, inv)

Pour avoir une matrice symétrique on cherche une procédure aléatoire qui nous donne un changement de base donné par une matrice orthogonale. Pour ce faire on utilise la fonction hess qui donne un changement de base orthogonal mettant une matrice sous une forme dite de Hessenberg. Bien sùr on ne maitrise pas alors la loi de la matrice aléatoire de changement de base.

                                                                                  
function A=defpos_sym(n,lmin,lmax)
  A=diag((lmax-lmin)*rand(N,1)+lmin);
  [U,H]=hess(rand(N,N));
  A=U*A*U';
endfunction

A=defpos_sym(N,2,3);
b=rand(N,1);

Une remarque: génériquement une matrice aléatoire (ici avec loi uniforme) est inversible :

 
ne=100;
for i=1:ne
  A1=rand(N,N);
  if rank(A1)<>N then pause;
  end;
end

Écrire une fonction Scilab qui calcule le critère (1) et une fonction qui calcule le gradient du critère.

 
function y=f(x,A,b)
  y = (1/2)* x'*A*x  + b'*x
endfunction
 
function y=df(x,A,b)
  y = (A+A')*x/2  + b;
endfunction

Programmer un algorithme de gradient à pas constant sur le problème quadratique. Il faudra évaluer numériquement la borne maximale du pas de gradient et choisir un critère d'arrêt. On pourra aussi tracer au cours des itérations l'évolution de la fonction coût et évaluer les temps de calculs (timer)

 
function rho_max=rmax(A)
  alpha = min(abs(spec((A+A')/2)))
  // valeur de Lipschitz du gradient
  C= norm((A+A')/2,2)
  // contrainte sur le pas de gradient
  rho_max= 2*alpha/C^2
endfunction

 
function [c,xn,fxn]=gradient(x0,f,df,rho,stop,nmax,A,b) 
// une méthode de gradient 
  c=[];
  xn = x0;
  for i=1:nmax 
    xnp1 = xn - rho*df(xn,A,b);
    fxn=f(xn,A,b);
    c=[c,fxn];
    if norm(xnp1-xn) < stop then return;end 
    xn = xnp1;
  end
  mprintf('Arret sur nombre maximum d''itérations %d',nmax) 
endfunction

Rendre le programme plus générique. On rajoute a la fonction gradient un dernier argument au nom prédéfini varargin. Lors de l'appel de la fonction gradient_1 définie ci dessous si plus de 6 arguments sont donnés en entrée, les arguments suplémentaires sont mis dans une liste et affecté a la variable varargin. Cela nous permet de passer des arguments à la fonction f et à la fonction df.

 
function [c,xn,fxn]=gradient_1(x0,f,df,rho,stop,nmax,varargin) 
// une méthode de gradient 
  c=[];
  xn = x0;
  for i=1:nmax 
    xnp1 = xn - rho*df(xn,varargin(:));
    fxn=f(xn,varargin(:));
    c=[c,fxn];
    if norm(xnp1-xn) < stop then return;end 
    xn = xnp1;
  end
  mprintf('Arret sur nombre maximum d''itérations %d',nmax) 
endfunction

Calculer la solution du problème d'optimisation revient ici à résoudre un système linéaire. On pourra comparer la solution du problème d'optimisation avec la solution obtenue en utilisant des algorithmes de résolution de systèmes linéaires de Scilab.

 

exec('optim_macros.sci'); 

N=10;

A=defpos_sym(N,2,3);
b=rand(N,1);

// le pas de gradient maximal 

rho_max = rmax(A)
// méthode de gradient 
x0= rand(N,1);
rho= rho_max/10;

// iterations de gradient 

[c,xn,fxn]=gradient(x0,f,df,rho,1.e-3,500,A,b);

// On peut calculer la solution du probleme 
// par résolution d'un système linéaire 

xs= A\(-b)   
fxs=f(xs,A,b); 

// test des resultats 

plot(c-fxs) 

// Rendre la fonction gradient plus générique 

[c,xn,fxn]=gradient_1(x0,f,df,rho,1.e-3,500,A,b);

plot(c-fxs)

1.1 Rajout d'une contrainte

On rajoute maintenant au problème d'optimisation une contrainte linéaire de la forme $Tx=0$. Pour que l'ensemble admissible ne soit pas réduit à $x=0$, il faut bien s'assurer que la matrice $T$ à un noyau de dimension non nulle.

Écrire une fonction qui tire de façon aléatoire un matrice N x N dont le rang est par exemple N/2 (indication : si M est une matrice n x m aléatoire quel est le rang générique de M*M' ? ).

 
function T=contrainte(N,p) 
// Une matrice aléatoire NxN de rang p
// pour rajouter des contraintes de la forme T*x = 0 
// T est une matrice NxN aléatoire dont le noyau est de dimension N/2 
  T=rand(N,p);
  T= T*T'; 
endfunction

Reprendre la première partie avec un nouveau critère d'optimisation ou on pénalise la contrainte $Tx=0$ en rajoutant au critère un terme $(1/(2\epsilon))* {\Vert Tx\Vert}^2$ :

$$\min_{x \in \mathbb{R}^{N}} \frac{1}{2} \left< x, Ax \right> + \left< b, x \right> + \frac{1}{2\epsilon} \left< Tx, Tx \right>$$ (2)

 
function y=fc(x,A,b,T,eps)
// la contrainte est de la forme T*x = 0 
// on utilise une penalisation 
  y = (1/2)* x'*A*x  + b'*x + (1/eps)*(1/2)*(T*x)'*T*x
endfunction

function y=dfc(x,A,b,T,eps)
    y = (A+A')/2*x  + b + (1/eps)*T*x
endfunction

On se reportera au lien plus bas pour le script de résolution dans le cas pénalisé.

On peut remarquer les contraintes linéaires que l'on a rajouté sont redondantes puisque la matrice est de taille N xN + et de rang N/2

1.2 Un peu d'algèbre linéaire

En utilisant la fonction colcomp (compression de colonnes) On peut obtenir une base du noyau de l'opérateur $T$. Cela permet d'écrire les vecteurs $x$ admissibles du problème avec contraintes $Tx=0$ sous la forme $x = W y$. On se ramène ainsi à un problème d'optimisation sans contraintes en $y$. Le programmer et comparer avec la section précédente.

L'idée ici est d'éliminer la contrainte $Tx=0$ en paramétrisant les élements du noyau de $T$ par $x = W y$ ou $W$ est une matrice dont les colonnes engendrent une base du noyau de $T$. Au lieu de minimiser en $x$ avec contrainte, on minimise en $y$ sans contraines et la solution $x^{\star}$ s'obtient alors à la fin par $x^{\star}= W y^{\star}$. La fonction Scilab colcomp permet de trouver la matrice $W$.

Que se passe-t-il si le rang de la matrice $T$ n'est pas égale au nombre de lignes de $T$ ? (c'est d'ailleurs ce qui se passe avec la méthode que nous avons utilisé pour obtenir T).

On peut remarquer les contraintes linéaires sont alors redondantes.

Se ramener à une structure de contrainte ou T est de rang plein (rowcomp).

Résoudre avec Scilab le système linéaire :

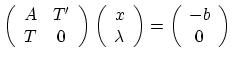$$\left( \begin{array}{cc} A & T' \\ T & 0 \end{array} \right) \lef... ...mbda \end{array} \right) = \left( \begin{array}{c} - b \\ 0 \end{array} \right)$$ (3)

Le système linéaire que l'on cherche à résoudre ici est une condition nécessaire d'optimalité du problème avec contrainte. La résolution de ce système nous donne un couple $(x^{\star},p^{\star})$, On remarque que si $T$ n'est pas de plein rang il n'y a pas unicité de $p^{\star}$, la matrice est singulière. La phase précédente utilisant rowcomp nous permet d'avoir un unique couple $(x^{\star},p^{\star})$ solution à notre système linéaire. On vérifie alors que $x^{\star}$ est bien la solution en comparant avec les sections précédentes.

T=contrainte(N,N/2) ; 

// verifions 
rank(T)

// la contrainte est de la forme T*x = 0 
// on utilise une penalisation 

eps = 0.1 ;
rho_max = rmax(A+ (1/eps)*T'*T); 

// méthode de gradient 

x0= rand(N,1);
rho= rho_max/10;

[c,xn,fxn]=gradient_1(x0,fc,dfc,rho,1.e-4,500,A,b,T,eps);

//  Un peu d'algèbre linéaire
//  pour résoudre le problème avec contraintes 
// ---------------------------- 

[W,rk]=colcomp(T);
// les rk premieres colonnes de W donne une base du noyau de T 
// x = W(:,1:rk)* y 

W1= W(:,1:rk); 

// On minimise sans contraintes avec un nouveau A 

A1= W1'*A*W1; 
b1 = W1'*b; 

// contraintes sur le pas de gradient 

rho_max  = rmax(A1); 

// méthode de gradient 
N1= size(A1,1) 
y0= rand(N1,1); yn=y0;
rho= rho_max/10;

[c,yn,fyn]=gradient_1(x0,f,df,rho,1.e-8,500,A,b);

ys= A1\(-b1) 
f(ys,A1,b1)
// on revient à xs 
xs= W1*ys ;
// norm(T*xs) 

// On change les contraintes pour rendres les lignes linéairement inépendantes 

T1= contrainte_plein_rang(T);
X= [ (A+A')/2, T1'; T1, zeros(N/2,N/2)] \ [ -b ; zeros(N/2,1)];

norm(X(1:N) -xs) 

// avec T 

X2 = [ (A+A')/2, T'; T, zeros(N,N)] \ [ -b ; zeros(N,1)];

// le systeme est singulier, la partie en lambda est 
// non unique. 

norm(X(1:N) -xs)

2 Programmes Scilab

• fonctions
• script

3 Optimisation avec contraintes

On cherche à nouveau à résoudre le problème de minimisation avec une contrainte mais en utilisant cette fois une dualisation des contraintes égalités. On va chercher un point selle du Lagrangien

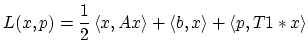$$L(x,p) = \frac{1}{2} \left< x, Ax \right> + \left< b, x \right> + \left< p, T1*x \right>$$ (4)

On utilisera les fonctions déjà écrite pour tirer aléatoirement une valeur pour A, b et T1. T1 désigne ici une matrice N/2xN de rang N/2 (donc de plein rang) obtenue à partir de T à l'aide de rowcomp.

En utilisant les sections précédentes on sait calculer une solution en x du problème avec contraintes.

Pour obtenir un point selle du problème en $L(u,p)$ à savoir un couple $(\overline{u},\overline{p})$ tels que $u \mapsto L(u,\overline{p})$ à un minimum en $u$ et $p \mapsto L(\overline{u},p)$ à un maximum en $p$. On va utiliser un algorithme d'Uzawa.

Soit $p_k$ fixé on cherche $u_k$ qui minimise $L(u,p_k)$ en utilisant un algorithme d'optimisation sans contrainte. Puis $p_{k+1}$ est calculé en utilisant un pas de méthode de gradient :

$$p_{k+1} = p_k + \rho L_{p}(u_k,p_k)$$

Programmer cet algorithme et tester numériquement sa convergence en jouant sur le paramètre $\rho$. Noter que la partie minimisation sans contraintes peut aussi être faite dans le cas quadratique par résolution d'un système linéaire. On pourra aussi programmer cette version pour comparer les résultats. On pourra aussi utiliser les sections précédentes pour calculer une solution.

// Minimisation de fonctionnelles quadratique
// avec contraintes egalité 

exec('optim_macros.sci'); 

N=10;

A=defpos_sym(N,2,3);
b=rand(N,1);

// Rajout d'une contrainte
// On rajoute une contrainte. de la forme T*x = 0 
// T est une matrice NxN aléatoire dont le noyau est de dimension N/2 
// ---------------------------

T=contrainte(N,N/2) ; 
T1= contrainte_plein_rang(T);

// la solution à trouver 

Xl= [ (A+A')/2, T1'; T1, zeros(N/2,N/2)] \ [ -b ; zeros(N/2,1)];
X=Xl(1:N)

// Usawa 
// L(u,p)= J(u) + <p,theta(u)> = (1/2)x'*A*x +b'*x + p'*T* x 

p=ones(N/2,1) 
rho_max = rmax(A)
// méthode de gradient 
x0= rand(N,1);
rho= rho_max/10;
rho_p = 1.e-3

c1=[];
for i=1:1000
  [c,xn,fxn]=gradient_1(x0,f,df,rho,1.e-6,500,A,b+T1'*p);
  p = p + rho_p * T1*xn;
  c1=[c1,f(xn,A,b)];
end

// Pour aller plus vite en se rappellant que 
// la minimisation a faire revient à résoudre un système linéaire 

p=ones(N/2,1) 
x0= rand(N,1);
c1=[];
for i=1:1000
  xn = A\(- (b+T1'*p));
  p = p + rho_p * T1*xn;
  c1 = [c1,f(xn,A,b)];
end

// autre test 

p=Xl(N+1:$) 
x0=Xl(1:N);
c1=[];
for i=1:1000
  xn = A\(- (b+T1'*p));
  p = p + rho_p * T1*xn;
  c1 = [c1,f(xn,A,b)];
end

3.1 Un cas particulier

Supposons ici que la partie $J(x) = \frac{1}{2} \left< x, Ax \right> + \left< b, x \right>$ se décompose en deux parties indépendantes

$$J(x=(x_1,x_2)) = \frac{1}{2} \left< x_1, A_1 x_1 \right> + \left<... ...1 \right> + \frac{1}{2} \left< x_2, A_2 x_2 \right> + \left< b_2, x_2 \right>$$

alors pour $p_k$ le problème de minimisation sans contraintes se décompose en deux problèmes indépendants. On se propose d'utiliser cela pour paralléliser l'exécution du programme.

4 quelques notes sur le parallélisme

On distingue habituellement quatre type principaux de parallélisme basées sur le flot des instructions (I) et sur le flot des données (D) SISD, SIMD, MISD, MIMD. De nos jours cette classification est un peu artificielle car les microprocesseurs courants incluent plusieurs formes de micro-parallélisme.

• SISD Machine de Von Neuman, une seule instruction, une seule donnée à chaque instant.
• SIMD La même instruction s'applique a des données différentes en parallèle. Par exemple une addition matricielle C=A+B ou N processeur s'occupent chacun d'une colonne de C.
• MISD Plusieurs instructions peuvent s'exécuter en même temps sur la même donnée. On trouve cela fréquemment dans les processeurs modernes: processeurs vectoriels et les architectures pipelines.
• MIMD C'est le cas que nous allons regardé avec Scilab. Deux types d'architectures à mémoire partagée ou à mémoire locale avec réseau de communication.

5 Scilab et PVM

PVM veut dire ``Parallel Virtual Machine''. PVM est constitué d'une librairie qui permet la communication par passage de messages et d'exécutables (machines dépendant) qui permettent de gérer les communications entre machines (pvmd3) et de contrôler les utilisateurs au sein d'une application PVM.

PVM est interfacé dans Scilab (help pvm) et la plupart des fonctions de contrôle de pvm peuvent être exécutées à partir de Scilab. Que ce soit le lancement des démons pvmd3, la création de processus, envoyer ou recevoir des objets Scilab, synchroniser des processus.

Noter qu'il peut parfois être utile de lancer une console pvm par
/usr/local/scilab/pvm3/lib/LINUX/pvm
pour contrôler l'état des machines intervenant dans un calcul avec PVM ou arrêter une machine virtuelle PVM.

Noter que faire tourner sur une unique machine plusieurs Scilab communiquant par PVM et menant a bien un calcul parallèle ou faire intervenir plusieurs machines différentes n'est pas fondamentalement différent. Ce qui veut dire que l'on peut dans un premier temps se limiter a une seule machine sur des données de petites tailles pour mettre au point un Algorithme.

6 Quelques instructions PVM en Scilab

• pvm_start démarre le démon pvm sur la machine.
• pvm_spawn démarre un ou plusieurs Scilab qui deviennent de nouveau processus dans la machine PVM. Les Scilab lancés exécutent le script passé en argument.
• pvm_send transmission de données Scilab a une ou plusieurs taches PVM.
• pvm_recv attente de données transmises.
• pvm_exit le Scilab qui execute pvm_exit quitte la machine virtuelle
• pvm_parent pour obtenir l'identificateur de la tache parente.
• pvm_halt terminer le démon PVM

7 Un premier exemple

On cherche à calculer $\int_0^1 4/(1+x^2) dx$ que l'on décompose en

$$\sum_{i=1}^N \int_{x_i}^{x_{i+1}} 4/(1+x^2) dx$$

Un programme maître Scilab décompose $[0,1]$ répartir les calculs entre plusieurs Scilab et recombine le tout pour obtenir le résultat cherché.

7.1 Le programme Maître

 
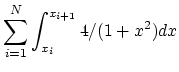
// je démarre pvm 
ok=pvm_start()       
if ok<>0 then disp('pvm daemon already active'),end;
// je lance N nouveaux scilab 
N=1;
x=linspace(0,1,N+1),
path=get_absolute_file_path('intg.master.sce');
[task_id,numt] = pvm_spawn(path+'/intg.slave.sce',N)
if numt<0 then disp(['pvm_spawn aborts to create a new process']); end 
for i=1:N 
  pvm_send(task_id(i),[x(i),x(i+1)],0);
end 

v=0;
for i=1:N
  v=v+ pvm_recv(task_id(i),0);
end 

x_message(['Job finished'])
pvm_halt()

// pvm_kill(task_id)

7.2 Le programme Esclave

mtid = pvm_parent();
X = pvm_recv(mtid,0)
printf("I am slave with parent %d\n",mtid);
// I start my job 
function y=f(x) ; y=4/(1+x^2) ; endfunction
v=intg(X(1),X(2),f);
pvm_send(mtid,v,0);
pvm_exit();
exit(0);

Notes

... Chancelier¹

Cermics, École Nationale des Ponts et Chaussées, 6 et 8 avenue Blaise Pascal, 77455, Marne la Vallée, Cedex 2