This page summarizes industrial grants on computational mechanics with EDF and with CEA over the last decade (PI: A. Ern).

Collaborations with EDF

• Compatible Discrete Operator (CDO) schemes
  • PhD of J. Bonelle (defended 2014), Compatible discrete operator schemes on polyhedral meshes for elliptic and Stokes equations
  • PhD of P. Cantin (defended 2016), Approximation of scalar and vector transport problems on polyhedral meshes
  • PhD of R. Milani (defended 2020), Compatible Discrete Operator schemes for the unsteady incompressible Navier-Stokes equations

• Reduced-order models (jointly with V. Ehrlacher)
  • PhD of A. Benaceur (defended 2018), Model reduction for nonlinear heat transfer and mechanics
  • PhD of I. Niakh (defended 2022), Model reduction for variational inequalities in computational mechanics

• Hybrid high-order (HHO) methods
  • PhD of N. Pignet (defended 2019), Hybrid High-Order methods for nonlinear solid mechanics

• Selected illustrations (deformed pipe, Hertz spheres in contact, pump under plastic deformations)
                                        

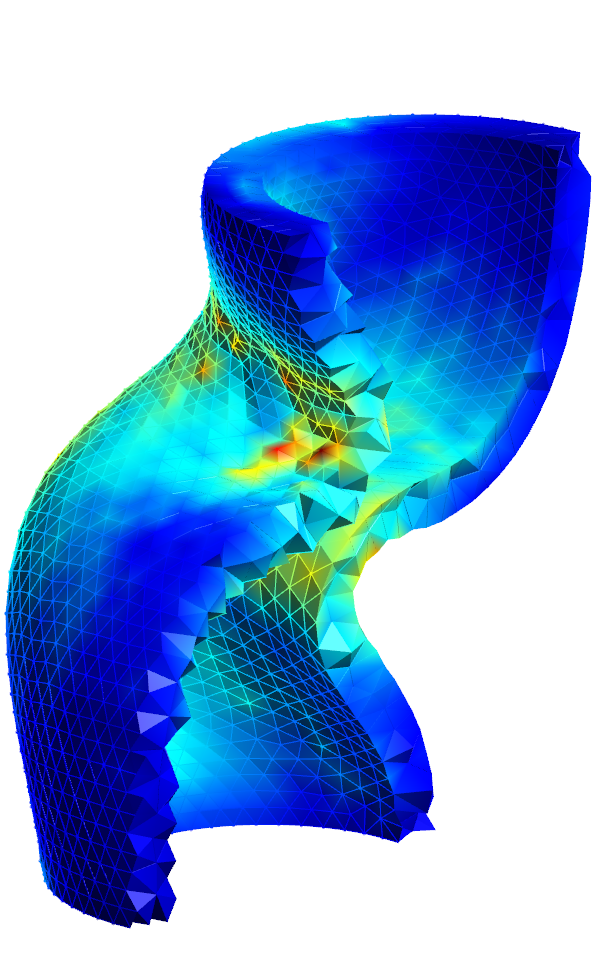
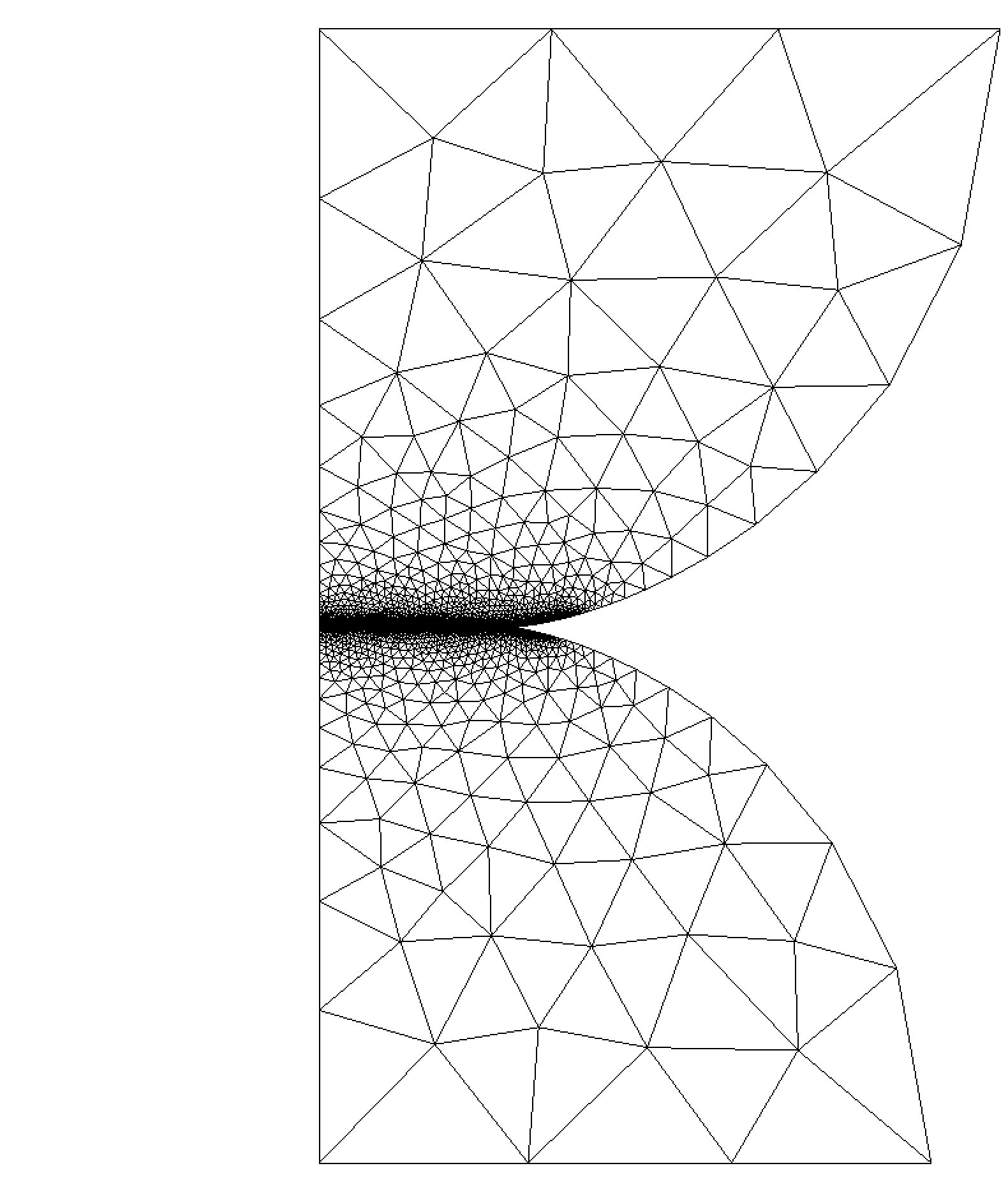
• Related publications
  • I. Niakh, G. Drouet, V. Ehrlacher, and A. Ern, A reduced basis method for frictional contact problems formulated with Nitsche's method, SMAI J. Comput. Math., 10, 29-54 (2024) [hal]
  • I. Niakh, G. Drouet, V. Ehrlacher, and A. Ern, Stable model reduction for linear variational inequalities with parameter-dependent constraints, ESAIM Math. Mod. Numer. Anal., 57(1), 167-189 (2023) [hal]
  • R. Milani, J. Bonelle and A. Ern, Artificial compressibility methods for the incompressible Navier-Stokes equations using lowest-order face-based schemes on polytopal meshes, Comput. Methods Appl. Math., 22(1), 133-154 (2022) [hal]
  • A. Benaceur, V. Ehrlacher and A. Ern, A reduced basis method for parametrized variational inequalities applied to contact mechanics, Int. J. Numer. Methods Eng., 121(6), 1170-1197 (2020) [hal]
  • F. Chouly, A. Ern and M. Pignet, A Hybrid high-order discretization combined with Nitsche's method for contact and Tresca friction in small strain elasticity SIAM J. Sci. Comput., 42(4), A2300-A2324 (2020) [hal]
  • M. Abbas, A. Ern and N. Pignet, A hybrid high-order method for incremental associate plasticity with small deformations, Comp. Meth. Appl. Mech. Eng., 346, 891-912 (2019) [hal]
  • M. Abbas, A. Ern and N. Pignet, A hybrid high-order method for finite elastoplastic deformations within a logarithmic strain framework, Int. J. Numer. Methods Eng., 120, 303-327 (2019) [hal]
  • M. Abbas, A. Ern and N. Pignet, Hybrid high-order methods for finite deformations of hyperelastic materials, Comput. Mech., 62(4), 909-938 (2018) [hal]
  • A. Benaceur, V. Ehrlacher, A. Ern and S. Meunier, A progressive reduced basis/empirical interpolation method for nonlinear parabolic problems, SIAM J. Sci. Comput., 40(5), A2930-A2955 (2018) [hal]
  • P. Cantin, J. Bonelle, E. Burman and A. Ern, A vertex-based scheme on polyhedral meshes for advection-reaction equations with sub-mesh stabilization, Comput. Math. Appl., 72(9), 2057-2071 (2016) [hal]
  • P. Cantin and A. Ern, Vertex-based Compatible Discrete Operator Schemes on polyhedral meshes for advection-diffusion equations, Comput. Methods Appl. Math., 16(2), 187-212 (2016) [hal]
  • J. Bonelle, D. Di Pietro and A. Ern, Low-order reconstruction operators on polyhedral meshes: Application to Compatible Discrete Operator schemes, Comput. Aided Geom. D., 35/36, 27-41 (2015) [hal]
  • J. Bonelle and A. Ern, Analysis of compatible discrete operator schemes for the Stokes equations on polyhedral meshes, IMA J. Numer. Anal. 35, 1672-1697 (2015) [hal]
  • J. Bonelle and A. Ern, Analysis of compatible discrete operator schemes for elliptic problems on polyhedral meshes, ESAIM Math. Mod. Numer. Anal., 48, 553-581 (2014) [pdf, copyright EDP Sciences and SMAI]

Collaborations with CEA

• Unfitted HHO methods
  • Postdoc of G. Delay (2018-19), Design and analysis of unfitted HHO for Poisson and Stokes equations

• HHO methods for wave propagation
  • Postdoc of O. Duran (2019-20), Design of HHO discretizations for wave equations in second- and first-order form
  • PhD of M. Steins (defended 2023), An explicit hybrid high-order method for structural dynamics
  • PhD of R. Mottier (defended planned in 2025), HDG/HHO methods for geophysical wave propagation

• Discrete element methods
  • PhD of F. Marazzato (defended 2020), Discrete element and time-integration methods for elasto-plasticity and dynamic cracking

• Selected illustrations (cracking of notched plate, wave around airfoil, acoustic wave across flower-like interface)
                                                   

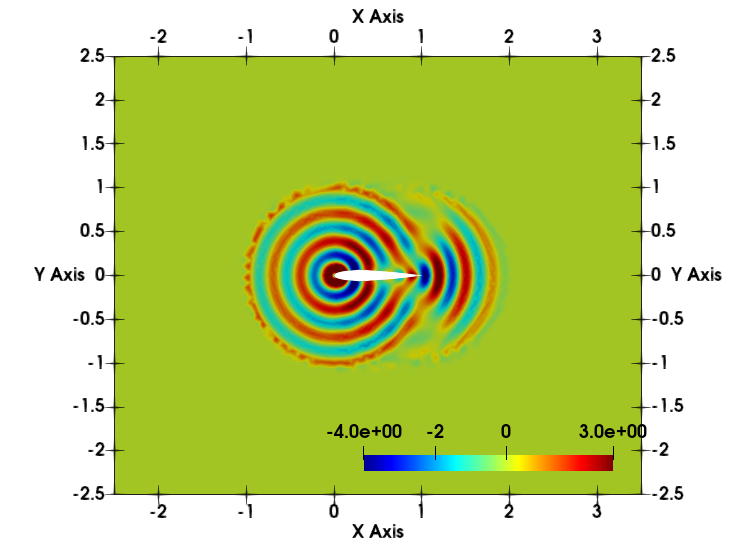
• Related publications
  • A. Ern and M. Steins, Convergence analysis for the wave equation discretized with hybrid methods in space (HHO, HDG and WG) and the leapfrog scheme in time, J. Sci. Comput., 101(1), Paper No. 7, 28 pp. (2024) [hal]
  • M. Steins, A. Ern, O. Jamond and F. Drui, Time-explicit Hybrid High-Order method for the nonlinear acoustic wave equation, ESAIM Math. Mod. Numer. Anal., 57(5), 2977-3006 (2023) [hal]
  • E. Burman, O. Duran, A. Ern, Hybrid high-order methods for the acoustic wave equation in the time domain, Commun. Appl. Math. Comput. (CAMC), 4(2), 597-633 (2022) [hal]
  • E. Burman, O. Duran, A. Ern, Unfitted hybrid high-order methods for the wave equation, Comp. Meth. Appl. Mech. Eng., 389, 114366 (2022) [hal]
  • F. Marazzato, A. Ern and L. Monasse, Quasi-static crack propagation with a Griffith criterion using a variational discrete element method, Comput. Mech., 69(2), 527-539 (2022) [hal]
  • E. Burman, M. Cicuttin, G. Delay and A. Ern, An unfitted hybrid high-order method with cell agglomeration for elliptic interface problems, SIAM J. Sci. Comput., 43(2), A859-A882 (2021) [hal]
  • E. Burman, G. Delay and A. Ern, An unfitted hybrid high-order method for the Stokes interface problem, IMA J. Numer. Anal., 41(4), 2362-2387 (2021) [hal]
  • E. Burman, O. Duran, A. Ern and M. Steins, Convergence analysis of hybrid high-order methods for the wave equation, J. Sci. Comput., 87(3), 91 (2021) [hal]
  • F. Marazzato, A. Ern and L. Monasse, A variational discrete element method for quasistatic and dynamic elastoplasticity, Int. J. Numer. Methods Eng., 121, 5295-5319 (2020) [hal]
  • F. Marazzato, A. Ern, C. Mariotti and L. Monasse, An explicit pseudo-energy conserving time-integration scheme for Hamiltonian dynamics, Comp. Meth. Appl. Mech. Eng., 347, 906-927 (2019) [hal]