Interpolation et approximation polynomiale
Licence de mathématiques Nouméa 2004

Jean-Philippe CHANCELIER
(avec le soutien du Ministère de l'Outre-Mer)
Version pdf de ce document
Version sans bandeaux

Table des matières

1 Interpolation polynomiale: matrice de Vandermonde

On cherche à résoudre le problème d'interpolation polynomiale par résolution du système linéaire obtenu en écrivant le système de $ n+1$ équations à $ n+1$ inconnues. On cherche donc l'unique polynôme de degré $ n$ passant par les points $ (x_i,f_i)_{i=0,\ldots,n}$. Les points $ (x_i)_{i=0,\ldots,n}$ étant tous distincts.

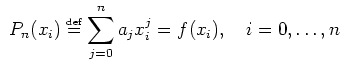$\displaystyle P_n(x_i) \stackrel{\mbox{\tiny def}}{=}\sum_{j=0}^{n} a_j x_i^j = f(x_i), \quad i=0,\ldots, n$ (1)

Soit en notation matricielle :

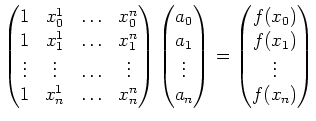$\displaystyle \begin{pmatrix}1 & x_0^1 & \ldots & x_0^n \ 1 & x_1^1 & \ldots ... ...pmatrix} = \begin{pmatrix}f(x_0) \ f(x_1) \ \vdots \ f(x_n) \end{pmatrix}$ (2)

    

Question 1   Écrire le code Scilab permettant de construire le polynôme d'interpolation par résolution du système linéaire utilisant le Vandermonde. On notera que la construction du Vandermonde peut se faire de façon vectorielle



    

Question 2   Utiliser le code précédent avec la fonction $ 1/(1+x^2)$ et des points d'interpolations régulièrement espacés sur $ [-5,5]$ et représenter graphiquement la fonction initiale et le polynôme d'interpolation. A partir de combien de points la résolution ne marche plus ? Explication ?



2 Polynôme d'interpolation de Lagrange

On utilise directement les polynômes de Lagrange pour réaliser l'interpolation polynomiale. Le $ i$-ème polynôme de Lagrange s'écrit :

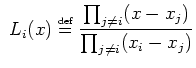$\displaystyle L_i(x) \stackrel{\mbox{\tiny def}}{=}\frac{ \prod_{j\ne i} (x-x_j)}{\prod_{j\ne i} (x_i-x_j)}$ (3)

Et le polynôme d'interpolation s'écrit alors :

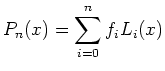$\displaystyle P_n(x) = \sum_{i=0}^n f_i L_i(x)$ (4)

    

Question 3   Écrire le code Scilab qui construit de polynôme d'interpolation de Lagrange par construction directe à partir des données $ (x_i,f(x_i))_{i=1,\ldots,n}$. Reprendre l'exemple du paragraphe précédent et comparer ? Que se passe-t-il quand le nombre de points d'interpolation augmente ?



3 Évaluation du polynôme d'interpolation de Lagrange par l'algorithme de Neville

Pour évaluer le polynôme d'interpolation en un point on peut utiliser l'algorithme de Neville que l'on rappelle ici. Cet algorithme permet en outre une estimation récursive quand on rajoute progressivement des points d'interpolation. Soit $ P_{i_0\ldots,i_k}$ le polynôme d'interpolation de degré $ k$ passant par les points $ (x_{i_p},f_{i_p})_{p=0,\ldots,k}$ on établit facilement la formule récursive suivante :

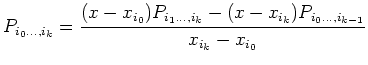$\displaystyle P_{i_0\ldots,i_k} = \frac{ (x-x_{i_0}) P_{i_1\ldots,i_k}- (x-x_{i_k}) P_{i_0\ldots,i_{k-1}}} {x_{i_k}-x_{i_0}}$ (5)

avec

$\displaystyle P_{i_\alpha} = f_{i_\alpha}$ (6)

Cette formule nous permet de calculer $ P_n(x) = P_{0,\ldots,n}(x)$ pour une valeur de $ x$ fixée.

    

Question 4   Programmer l'algorithme de Neville pour évaluer la valeur du polynôme d'interpolation en un point x. Puis le rendre vectoriel pour évaluer directement la valeur du polynôme pour $ n$ valeurs de $ x$ données dans un vecteur.



4 Différences divisées

L'algorithme de Neville est utilisé pour obtenir la valeur du polynôme d'interpolation en un point. Quand on cherche l'expression du polynôme on peut utiliser les différences divisées et la formule d'interpolation de Newton. On cherche le polynôme d'interpolation sous la forme :

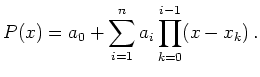$\displaystyle P(x) = a_0 + \sum_{i=1}^{n} a_i \prod_{k=0}^{i-1}(x-x_k) .$ (7)

Les différences divisées se définissent alors par 

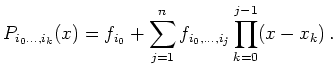$\displaystyle P_{i_0\ldots,i_k}(x) = f_{i_0} + \sum_{j=1}^{n} f_{i_0,\ldots,i_j} \prod_{k=0}^{j-1}(x-x_k) .$ (8)

De la formule de récursion sur les polynômes $ P_{i_0\ldots,i_k}$ on déduit, en identifiant les termes de plus haut degrés, une formule de récursion sur les différences divisées :

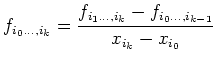$\displaystyle f_{i_0\ldots,i_k} = \frac{ f_{i_1\ldots,i_k}- f_{i_0\ldots,i_{k-1}}}{x_{i_k}-x_{i_0}}$ (9)

    

Question 5   Programmer la construction du polynôme d'interpolation aux moyens des différences divisées. On notera que pour $ n$ grand, une évaluation numérique des valeurs du polynôme obtenu par la formule d'interpolation de Newton par la fonction horner donne de meilleurs résultats que la même évaluation à partir du polynôme d'interpolation de Lagrange (utiliser la fonction $ 1/(1+x^2)$ sur $ [-1,1]$ )



    

Question 6   La formule de Newton permet une construction séquentielle des polynômes d'interpolation en rajoutant au fur et a mesure des points. Écrire une fonction qui met a jour et dessine les polynôme d'interpolation les point d'interpolation successifs étant obtenus en cliquant sur la fenêtre graphique.



5 Fonction de Lebesgue, points de Tchebychev

On regarde dans ce paragraphe le comportement de $ \omega(x) = \left\vert \prod_{i=0}^n (x-x_i) \right\vert$ sur l'intervalle $ [-1,1]$ en fonction du choix des points $ x_i$. On regarde le cas des points régulièrement espacés et le cas des points de Tchebychev :

$\displaystyle x_i = \cos( \pi(2k+1)/(2(n-1)+2))\quad k=0,\ldots,n-1$ (10)

On fait de même pour la fonction de Lebesgue :

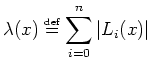$\displaystyle \lambda(x) \stackrel{\mbox{\tiny def}}{=}\sum_{i=0}^{n} \vert L_i(x)\vert$ (11)

    

Question 7   Tracer la fonction $ \omega(x)$ pour des points $ x_i$ régulièrement espacés sur [-1,1] et pour les points de Tchebychev. Faites de même pour la fonction de Lebesgue. Que constatez vous ?



6 Approximation en norme $ L^{\infty }$ polynômes de Bernstein

On cherche ici à approximer une fonction sur $ [0,1]$ par les polynômes de Bernstein :

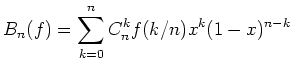$\displaystyle B_n(f) = \sum_{k=0}^{n} C_n^k f(k/n) x^k (1-x)^{n-k}$ (12)

On utilise le fait que pour $ x$ fixé dans $ [0,1]$ les coefficients $ C_n^k x^k (1-x)^{n-k}$ sont les probabilités d'une loi binomiale. La fonction Scilab binomial(x,n-1) est utilisée pour leurs calculs.

    

Question 8   Programmer le calcul des polynômes de Bernstein approchant une fonction continue sur $ [-1,1]$. Faites varier le degré du polynôme de Bernstein et superposez graphiquement la fonction et son approximation. Que constatez vous ?