On cherche à résoudre le problème d'interpolation polynomiale
par résolution du système linéaire obtenu en écrivant le
système de 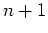 équations à
équations à 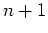 inconnues. On cherche donc
l'unique polynôme de degré
inconnues. On cherche donc
l'unique polynôme de degré 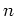 passant par les points
passant par les points
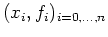 .
Les points
.
Les points
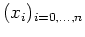 étant tous distincts.
étant tous distincts.
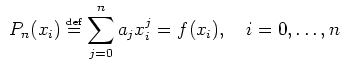 |
(1) |
Soit en notation matricielle :
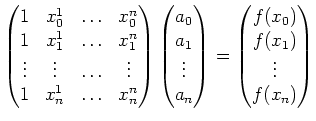 |
(2) |
->function y=f(x)

La fonction que l'on cherche à interpoler
-> y=10./(1+x.*x)
->endfunction
->n=5 ;
->x=linspace(-5,5,n)';

Les points d'interpolation régulièrement espacés
->V=(x*ones(1,n)).^( ones(n,1)*[0:n-1]);

Construction de la matrice de Vandermonde
->F=f(x);

Les points d'interpolation
(x,F)
->a = V F

Résolution du système linéaire
a =
! 1. !
! 2.469D-17 !
! - 0.1710875 !
! - 9.876D-19 !
! 0.0053050 !
->Pn=poly(a,"x","coeff")

Construction du polynome d'interpolation
Pn =
2 3 4
1 + 2.469D-17x - 0.1710875x - 9.876D-19x + 0.0053050x
->nr=200;
->xr=linspace(-5,5,nr)';
->yr=f(xr);
->yp=horner(Pn,xr);

Évaluation du polynôme aux points
xr avec
horner
->xbasc();
->plot2d1("onn",xr,[yr,yp])

Voir figure
1
->plot2d(x,F,-2);
Figure:
Interpolation 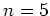 par résolution du système linéaire
par résolution du système linéaire
|
|
Noter que le conditionnement du Vandermonde se dégrade très vite si l'on
augmente le nombre de points et que le système linéaire devient numériquement
singulier pour 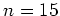 par exemple :
par exemple :
->vcond=[];
->for n=[5,10,20]
-> x=linspace(-5,5,n)';
-> V=(x*ones(1,n)).^( ones(n,1)*[0:n-1]);
-> vcond=[vcond,cond(V)];
->end
->mprintf('n=5 %5.3e, n=10 %5.3e, n=20 %5.3e',vcond);
 Conditionnement pour
Conditionnement pour 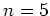 ,
, 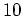 et
et 
n=5 9.043e+02, n=10 5.083e+06, n=20 4.874e+14
On utilise directement les polynômes de Lagrange pour réaliser
l'interpolation polynomiale. Le 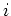 -ème polynôme de Lagrange s'écrit :
-ème polynôme de Lagrange s'écrit :
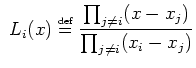 |
(3) |
Et le polynôme d'interpolation s'écrit alors :
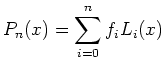 |
(4) |
->for n=5:20
-> x=linspace(-5,5,n)';

Les points d'interpolation régulièrement espacés
-> F=f(x);

Les points d'interpolation
(x,F),
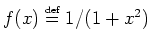
-> clear P;
-> for i=1:n
-> y=x; y(i)=[];

Les
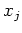
en retirant le
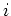
-ème
-> P(i)= poly(y,"x");
-> P(i)= P(i)/horner(P(i),x(i));

Le
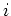
-ème polynôme de Lagrange
-> end
-> Pn= F'*P;

Le polynôme d'interpolation
-> nr=200;
-> xr=linspace(-5,5,nr)';
-> yr=f(xr);
-> yp=horner(Pn,xr);
-> xbasc();
-> plot2d1("onn",xr,[yr,yp])
-> plot2d(x,F,-2);

Voir figure
2 pour
n=13
-> Norme(n) =maxi(abs(yr-yp));

Un estimé de
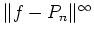
->end
->xbasc()
->plot2d(Norme)

Voir figure
3
Figure:
Interpolation 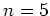 par construction des polynômes de Lagrange
par construction des polynômes de Lagrange
|
|
Figure:
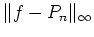 en fonction de
en fonction de 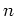
|
|
Pour évaluer le polynôme d'interpolation en un point on peut utiliser l'algorithme
de Neville que l'on rappelle ici. Cet algorithme permet en outre une estimation
récursive quand on rajoute progressivement des points d'interpolation. Soit
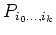 le polynôme d'interpolation de degré
le polynôme d'interpolation de degré 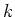 passant par les
points
passant par les
points
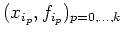 on établit facilement la formule
récursive suivante :
on établit facilement la formule
récursive suivante :
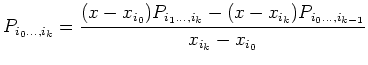 |
(5) |
avec
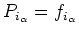 |
(6) |
Cette formule nous permet de calculer
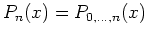 pour une valeur de
pour une valeur de 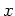 fixée. Le programme qui suit implémente l'algorithme de Neville, en travaillant
de façon vectorielle sur un ensemble de valeurs
fixée. Le programme qui suit implémente l'algorithme de Neville, en travaillant
de façon vectorielle sur un ensemble de valeurs xnev pour lesquelles on souhaite
obtenir la valeur de 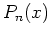 :
:
->n=6;
->x=linspace(-5,5,n)';

Les points d'interpolation régulièrement espacés
->F=f(x);

Les points d'interpolation
(x,F),
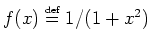
->xnev= 1:3;

Les points pour lesquels on veut la valeur de
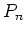
->xc=ones(n,1)*xnev - x*ones(1,size(xnev,'*'));

Matrice
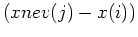
->xd=x*ones(1,size(xnev,'*')) ;
-> Chaque colonne de la matrice
col correspond aux
-> itérations de l'algorithme de Neville pour une valeur fixée de x (
xnev(j)).
-> A la fin des itérations
col est un vecteur ligne
->col=F*ones(1,size(xnev,'*'));

Démarrage de la récursion
->for k=1:n-1
-> col= xc(1:$-k,:).*col(2:$,:) - xc((1+k):$,:).*col(1:$-1,:);
-> col= col0./ (xd((1+k):$,:)-xd(1:$-k,:));

Mise à jour (le nombre de lignes de
col diminue de
1
->end
->clear P;
->for i=1:n
-> y=x; y(i)=[]; P(i)= poly(y,"x"); P(i)= P(i)/horner(P(i),x(i));
->end
->Pn= F'*P;
->y=horner(Pn,xnev);

Comparons avec l'interpolation de Lagrange
->if norm(y-col) > 10*%eps then pause;end
L'algorithme de Neville est utilisé pour obtenir la valeur du polynôme d'interpolation
en un point. Quand on cherche l'expression du polynôme on peut utiliser les différences
divisées et la formule d'interpolation de Newton. On cherche le polynôme d'interpolation
sous la forme :
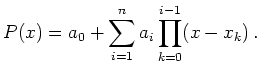 |
(7) |
Les différences divisées se définissent alors par
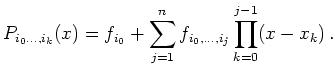 |
(8) |
De la formule de récursion sur les polynômes
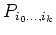 on déduit, en identifiant les
termes de plus haut degrés, une formule de récursion sur les différences divisées :
on déduit, en identifiant les
termes de plus haut degrés, une formule de récursion sur les différences divisées :
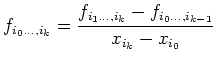 |
(9) |
Le programme qui suit mets en  uvre cette récursion pour construire en Scilab
le polynôme d'interpolation. On notera aussi que cette formulation permet à nouveau
une construction récursive.
uvre cette récursion pour construire en Scilab
le polynôme d'interpolation. On notera aussi que cette formulation permet à nouveau
une construction récursive.
->n=5;
->x=linspace(-5,5,n)';

Les points d'interpolation régulièrement espacés
->F=f(x);

Les points d'interpolation
(x,F),
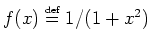
->clear P;
->for i=1:n-1
-> P(i)= poly(x(1:i),"x");

La base des polynômes pour la formule de Newton
->end
->P=[1;P]
P =
! 1 !
! !
! 5 + x !
! !
! 2 !
! 12.5 + 7.5x + x !
! !
! 2 3 !
! 12.5x + 7.5x + x !
! !
! 2 3 4 !
! - 31.25x - 6.25x + 5x + x !
->

On utilise la formule de récursion en conservant les
->

premiers termes de chaque colonnes qui seront les coefficients du polynôme
->col=F;
->coefP= col(1)*ones(n-1,1);
->for k=1:n-1
-> col= col(2:$) - col(1:$-1);
-> col= col0./ (x((1+k):$)-x(1:$-k));
-> coefP(k+1)=col(1);
->end
->Pn = coefP'*P;

Le polynôme d'interpolation
->nr=200;
->xr=linspace(-5,5,nr)';
->yr=f(xr);
->yp=horner(Pn,xr);
->pause;xbasc();
plot2d1("onn",xr,[yr,yp])
plot2d(x,F,-2);

Voir figure
4
Figure:
Interpolation par différences divisées
|
|
On notera que pour 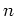 grand, une évaluation numérique des valeurs du polynôme
obtenu par la formule d'interpolation de Newton par la fonction
grand, une évaluation numérique des valeurs du polynôme
obtenu par la formule d'interpolation de Newton par la fonction horner
donne de meilleurs résultats que la même évaluation à partir du polynôme d'interpolation de
Lagrange (utiliser la fonction 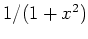 )
)
Le programme suivant montre l'aspect séquentiel de la construction par différence
divisées. L'utilisateur rentre les points uns à uns en cliquant, le polynôme
d'interpolation est mis à jours séquentiellement et un graphe est dessiné.
->function Pplot(a,b,npts,P)
-> xr=linspace(a,b,npts)';
-> yp=horner(P,xr);
-> plot2d1("onn",xr,yp,1,"000")
->endfunction
->P=[1];
->x=[];F=[];
->while %t
-> plot2d([],[],0,rect=[0,0,1,1])
-> if x<>[]
-> plot2d(x,F,-2,"000");
-> end
-> [but,xnew,fnew]=xclick();
-> xbasc();
-> if but==2 then ; break;end
-> x=[x;xnew];
-> F=[F;fnew];
-> if size(x,'*') <> 1 ;
-> P($+1)= poly(x(1:$-1),"x");
-> [m,n]=size(mat);
-> mat=[mat,zeros(m,1);zeros(1,n+1)];
-> mat(n+1,1)=F($);
-> for j=2:n+1
-> mat(n+1,j)= (mat(n+1,j-1)-mat(n,j-1))/(x(n+1)-x(n+1-j+1));
-> end
-> Pn = diag(mat)'*P;
-> else
-> mat=[F];
-> Pn = F;
-> end
-> Pplot(0,1,100,Pn);
->end
On regarde dans ce paragraphe le comportement de
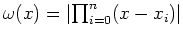 sur
l'intervalle
sur
l'intervalle ![$ [-1,1]$](img43.png) en fonction du choix des points
en fonction du choix des points 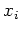 . On regarde le cas des points
régulièrement espacés et le cas des points de Tchebychev :
. On regarde le cas des points
régulièrement espacés et le cas des points de Tchebychev :
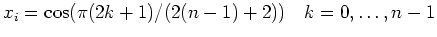 |
(10) |
On fait de même pour la fonction de Lebesgue :
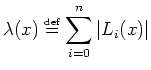 |
(11) |
->n=10;
->x=linspace(-1,1,n)';

Les points d'interpolation régulièrement espacés
->xcheb= cos( %pi*(2*(0:n-1)+1)/(2*(n-1)+2));

Les points de Tchebychev
->w=poly(x,"x");

Le polynôme
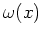
pour les points régulièrement espacés
->wcheb=poly(xcheb,"x")

Le polynôme
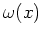
pour les points de Tchebychev
wcheb =
2 3
- 0.0019531 - 2.408D-17x + 0.0976562x + 4.341D-16x
4 5 6 7
- 0.78125x - 6.767D-16x + 2.1875x + 3.761D-15x
8 9 10
- 2.5x - 1.110D-16x + x
->nr=200;
->xr=linspace(-1,1,nr)';
->yr=abs(horner(w,xr));
->yp=abs(horner(wcheb,xr));
->xbasc();
->plot2d1("onn",xr,[yr,yp])

Voir figure
5
->clear P;
->for i=1:n
-> y=x; y(i)=[]; P(i)= poly(y,"x"); P(i)= P(i)/horner(P(i),x(i));
->end
->clear P1;
->for i=1:n
-> y=xcheb; y(i)=[]; P1(i)= poly(y,"x"); P1(i)= P1(i)/horner(P1(i),xcheb(i));
->end
->function y=lebesgue(x,P)

La fonction de Lebesgue
-> y=abs(horner(P,x)); y=sum(y,'r');
->endfunction
->nr=200;
->xr=linspace(-1,1,nr);
->yr=lebesgue(xr,P);
->yrcheb=lebesgue(xr,P1);
->pause;xbasc();
plot2d1("onn",xr',[yr;yrcheb]')

Voir figure
6
Figure 5:
Fonction 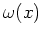
|
|
Figure 6:
Fonction de Lebesgue
|
|
On cherche ici à approximer une fonction sur ![$ [0,1]$](img49.png) par les polynômes de Bernstein :
par les polynômes de Bernstein :
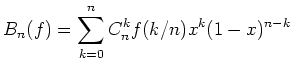 |
(12) |
On utilise le fait que pour 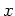 fixé dans
fixé dans ![$ [0,1]$](img49.png) les coefficients
les coefficients
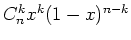 sont les
probabilités d'une loi binomiale. La fonction Scilab
sont les
probabilités d'une loi binomiale. La fonction Scilab binomial(x,n-1) est utilisée pour leurs
calculs.
->function y=f(x)
-> y=sin(5*%pi*x)0./ (1+ 25*x.*x)
->endfunction
->nr=200;
->xr=linspace(0,1,nr)';

Les valeurs de
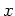
pour lesquelles on veut évaluer
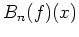
->yr=f(xr);
->for n=5:20:200
-> x=linspace(0,1,n)';
-> F=f(x);
-> Bnf=ones(xr);
-> for i=1:nr
-> Bnf(i) = binomial(xr(i),n-1)* F;

Valeur du
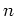
-ième polynôme de Bernstein pour
x=xr(i)
-> end
-> plot2d1("onn",xr,[yr,Bnf]);

Voir figure
7
->end
Figure:
Une fonction et son approximation par un polynôme de Bernstein 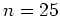
|
|
On retrouve de façon directe avec la construction des polynômes de Bernstein
la densité pour la norme infinie des polynômes dans les fonction continues sur ![$ [-1,1]$](img43.png) .
.
![]() équations à
équations à ![]() inconnues. On cherche donc
l'unique polynôme de degré
inconnues. On cherche donc
l'unique polynôme de degré ![]() passant par les points
passant par les points
![]() .
Les points
.
Les points
![]() étant tous distincts.
étant tous distincts.
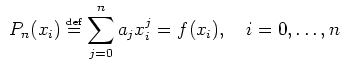
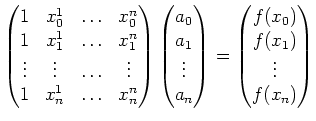
![]() par exemple :
par exemple :
![]() -ème polynôme de Lagrange s'écrit :
-ème polynôme de Lagrange s'écrit :
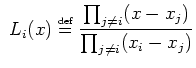
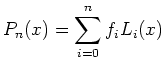
![]() le polynôme d'interpolation de degré
le polynôme d'interpolation de degré ![]() passant par les
points
passant par les
points
![]() on établit facilement la formule
récursive suivante :
on établit facilement la formule
récursive suivante :
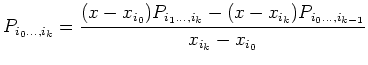
![]() pour une valeur de
pour une valeur de ![]() fixée. Le programme qui suit implémente l'algorithme de Neville, en travaillant
de façon vectorielle sur un ensemble de valeurs
fixée. Le programme qui suit implémente l'algorithme de Neville, en travaillant
de façon vectorielle sur un ensemble de valeurs ![]() :
:
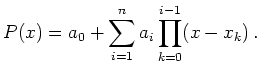
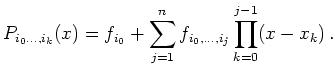
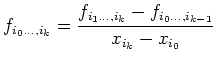
![]() uvre cette récursion pour construire en Scilab
le polynôme d'interpolation. On notera aussi que cette formulation permet à nouveau
une construction récursive.
uvre cette récursion pour construire en Scilab
le polynôme d'interpolation. On notera aussi que cette formulation permet à nouveau
une construction récursive.
![]() grand, une évaluation numérique des valeurs du polynôme
obtenu par la formule d'interpolation de Newton par la fonction
grand, une évaluation numérique des valeurs du polynôme
obtenu par la formule d'interpolation de Newton par la fonction ![]() )
)
![]() sur
l'intervalle
sur
l'intervalle ![]() en fonction du choix des points
en fonction du choix des points ![]() . On regarde le cas des points
régulièrement espacés et le cas des points de Tchebychev :
. On regarde le cas des points
régulièrement espacés et le cas des points de Tchebychev :
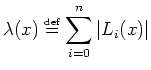
![]() par les polynômes de Bernstein :
par les polynômes de Bernstein :
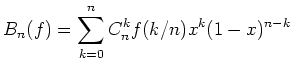
![]() fixé dans
fixé dans ![]() les coefficients
les coefficients
![]() sont les
probabilités d'une loi binomiale. La fonction Scilab
sont les
probabilités d'une loi binomiale. La fonction Scilab ![]() .
.