Soit ![]() un polynôme de degré
un polynôme de degré ![]() :
:
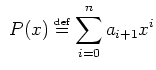
Soit ![]() les coefficients du polynôme
les coefficients du polynôme ![]() :
:
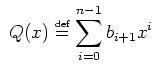 |
(2) |
Cet Algorithme s'appelle algorithme d'Horner, il revient à évaluer la valeur du polynôme ![]() en le factorisant sous la forme :
en le factorisant sous la forme :
Nous avons noté que la dérivée de ![]() au point
au point ![]() s'obtient en évaluant
s'obtient en évaluant
![]() . Il suffit donc de réappliquer l'algorithme d'Horner au polynôme
. Il suffit donc de réappliquer l'algorithme d'Horner au polynôme ![]() pour évaluer
pour évaluer ![]() .
.
Question 1
Écrire une fonction
[Q,R]=Horner(P,xi) qui calcule la décomposition
(Q,R) du polynôme horner et derivat. |
En fait, on peut calculer directement les valeurs ![]() et
et ![]() sans
passer par l'intermédiaire de la construction du polynôme
sans
passer par l'intermédiaire de la construction du polynôme ![]() , c'est à dire sans
stocker les coefficients du polynôme
, c'est à dire sans
stocker les coefficients du polynôme ![]() . On écrit conjointement les
deux algorithmes de Horner et pour faciliter la gestion des indices on initialise
le deuxième avec
. On écrit conjointement les
deux algorithmes de Horner et pour faciliter la gestion des indices on initialise
le deuxième avec ![]() plutôt que
plutôt que
![]() . Ainsi les deux vecteurs de
coefficients à calculer auront même taille :
. Ainsi les deux vecteurs de
coefficients à calculer auront même taille :
| (4) |
Question 2
Écrire une fonction
[val]=Hornerp(P,xi,p) qui calcule
val.
On pourra à nouveau tester le code en utilisant les primitives Scilab horner et derivat. |
Supposons que l'on ait estimé un zéro ![]() du polynôme
du polynôme ![]() ,
dans la décomposition de
,
dans la décomposition de
![]() on doit avoir
on doit avoir ![]() et la méthode de
Horner permet d'éliminer la racine
et la méthode de
Horner permet d'éliminer la racine ![]() du polynôme
du polynôme ![]() puisqu'elle donne
les coefficients du polynôme
puisqu'elle donne
les coefficients du polynôme ![]() . Mais si
. Mais si ![]() est une racine de
est une racine de ![]() on
doit aussi avoir
on
doit aussi avoir ![]() dans l'algorithme de Horner.
dans l'algorithme de Horner.
On peut donc utiliser la récurrence (3) à partir de de
![]() (méthode forward) ou à partir de
(méthode forward) ou à partir de ![]() méthode backward.
Si l'on cherche à éliminer successivement les racines d'un polynôme en éliminant
à chaque fois la plus grande racine, la méthode backward donne une meilleur stabilité
numérique.
méthode backward.
Si l'on cherche à éliminer successivement les racines d'un polynôme en éliminant
à chaque fois la plus grande racine, la méthode backward donne une meilleur stabilité
numérique.
On peut comparer les deux méthodes avec le polynôme
![]() en utilisant
la fonction
en utilisant
la fonction roots de Scilab pour estimer les valeurs des racines.
Question 3
Écrire les deux fonctions
[Q]=deflate_forward(P,xi)
[Q]=deflate_backward et les utiliser pour factoriser le polynôme
roots. |
L'équation (3) permettant de calculer les coefficients
du polynôme ![]() peut-être vu comme un système dynamique discret.
La stabilité de ce système ou de celui obtenu pour le calcul simultané de
peut-être vu comme un système dynamique discret.
La stabilité de ce système ou de celui obtenu pour le calcul simultané de
![]() et de ses dérivées au point
et de ses dérivées au point ![]() dépend de
dépend de ![]() . Pour
. Pour ![]() le
système est instable et on va donc pour des polynômes de grande taille
amplifier les erreurs de calcul si l'on utilise (3).
Mais on peut remarquer que
le
système est instable et on va donc pour des polynômes de grande taille
amplifier les erreurs de calcul si l'on utilise (3).
Mais on peut remarquer que ![]() s'écrit aussi :
s'écrit aussi :
Question 4
Écrire l'algorithme de Horner backward pour estimer la valeur d'un polynôme
et de sa dérivée première en un point
|
On utilise ici la méthode de Newton pour trouver les zéros d'un polynôme.
Soit ![]() un polynôme de degré
un polynôme de degré ![]() , on utilise pour trouver les
zéros l'algorithme de Newton qui consiste à effectuer les itérations suivantes :
, on utilise pour trouver les
zéros l'algorithme de Newton qui consiste à effectuer les itérations suivantes :
| (6) |
Il faut pouvoir évaluer la valeur du polynôme et de sa dérivée au point courant
![]() et nous avons vu qu'un algorithme d'Horner permet d'évaluer ces deux
quantités.
et nous avons vu qu'un algorithme d'Horner permet d'évaluer ces deux
quantités.
La convergence de l'algorithme de Newton dans ce cas particulier est donnée par le théorème suivant :
On trouvera la preuve de la convergence dans [1].
Pour implémenter cet algorithme il faut trouver un majorant de ![]() . Plusieurs
formules de majoration sont données dans la littérature. Par exemple :
. Plusieurs
formules de majoration sont données dans la littérature. Par exemple :
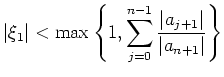 si si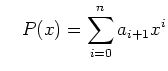 |
(7) |
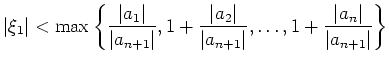 si si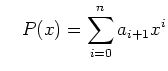 |
(8) |
Question 5
Programmer l'algorithme de Newton et le tester sur le polynôme :
|
En éliminant à chaque fois la plus grande racine trouvée on peut chercher
toutes les racines du polynôme ![]() . On peut constater dans le code
qui suit que la méthode d'élimination choisie (forward ou backward)
n'est pas anodine !
. On peut constater dans le code
qui suit que la méthode d'élimination choisie (forward ou backward)
n'est pas anodine !
Question 6
Programmer la recherche de toutes les racines du polynôme :
[Q]=deflate_forward(P,xi) et [Q]=deflate_backward.
Comparer les résultats |
Plutôt que d'essayer de simplifier le polynôme ![]() on peut utiliser
la méthode de Maehly (1954) qui consiste à appliquer la méthode de
Newton à la fraction rationnelle
on peut utiliser
la méthode de Maehly (1954) qui consiste à appliquer la méthode de
Newton à la fraction rationnelle
![]() plutôt que d'éliminer la
racine
plutôt que d'éliminer la
racine ![]() du polynôme
du polynôme ![]() . Ainsi si l'on a estimé les
. Ainsi si l'on a estimé les ![]() premières
racines du polynôme, notées
premières
racines du polynôme, notées ![]() ,
on cherche la
,
on cherche la ![]() -ème racine par l'algorithme de Newton :
-ème racine par l'algorithme de Newton :
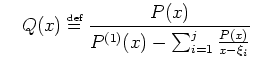 |
(9) |
Pour initialiser l'algorithme, on peut utiliser la dernière racine trouvée (à epsilon près pour éviter une division par zéro).
Question 7
Programmer la recherche de toutes les racines du polynôme :
|