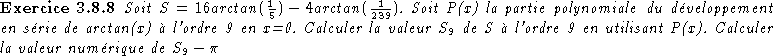Calcul de sommes, de produits, de séries et développements limités

• Sommes et produits : sum(f,i=0..n); product(f,i=0..n);. Calculez par exemple : , et .
• calcul de séries: taylor, mtaylor (readlib), laurent (readlib), series, Mclaurin.

  > s := series(sqrt(sin(x)), x=0, 4);

  On impose l'ordre du développement en donnant une valeur à la variable globale Order:=6; (par défaut) On fera attention au point suivant Maple donne des " grand O ".

  Si le développement obtenu est polynomial suivit d'un " grand O ", on le transforme en polynôme avec convert(",polynom);. Sinon, on peut éliminer le " grand O " avec eval(subs(O=0,s));

  Pour reconnaitre que sont les premiers termes du développement de cos(x) en série, aller chercher gfun dans la librairie share :

  > with(share): readshare(gfun,calculus): with(gfun):
  > s:= [ seq((-1)^k/(2*k)!, k=0..7) ];
  > guessgf(s,t);

  

  Correction:

  > series(sin(x),x=0,10);
  > map(series,[sin(x),cos(x),tan(x),arcsin(x),arccos(x),arctan(x),sec(x)],x+0,10);

  

  Correction:

  > taylor(sinh(sin(x))-sin(sinh(x)),x=0,16);

  

  Correction:

  > S:=series(x^x,x=1,11);
  > DL:=eval(subs(O=0,S));
  > readlib(coeftayl): eval(coeftayl(x^x,x=1,20));

  

  Correction:

  > s1:=0: for n to 100 do s1:=s1+exp(n*x) od;
  > s2:= convert([seq(exp(x*n),n=1..100)],`+`);
  > s3:= sum(exp(x*n),n=1..100);  # essayer avec un nombre < 100 !!!

  

  Correction:

  > series(1/GAMMA(x),x=infinity);
  > asympt(1/GAMMA(x),x);

  

  Correction:

  > readlib(mtaylor);
  > mtaylor(1/(1-2*r*cos(theta)+r^2),[r=0,theta=Pi]);

  On peut enfin obtenir un développement limité au voisinage d'un point pour une fonction définie implicitement :

  > # Une utilisation de RootOf 
  > series( RootOf(y*exp(y)=y^5+ln(1+x),y),x);

• calcul de limites: ex : lim(sin(x)/x,x=0), lim(Heavyside,x=0,left).

  

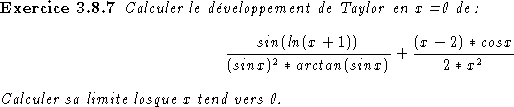
  Correction:

  > expr:=sin(ln(x+1))/((sin(x))^2 *arctan(sin(x))) + ((x-2) *cos(x))/(2* x^2);
  > taylor(expr,x=0);
  > limit(expr,x=0);

   

  Correction:

  > a9:=series(arctan(x),x=0,10);
  > a9:=convert(a9,polynom);
  > s9:=16*subs(x=1/5,a9)-4*subs(x=1/239,a9);
  > evalf(s9-Pi);