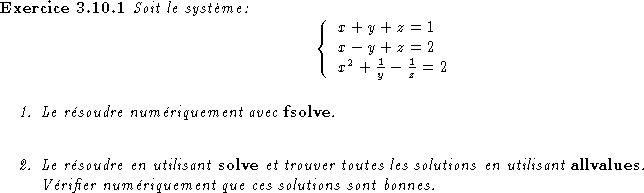
Résolution d'équations: solve, dsolve, linsolve, fsolve, rsolve, isolate (readlib)
> solve(x^3+p*x+q=0,x);
> # fsolve(....
> rsolve(f(n)=f(n-1)+f(n-2),f);
> deq:= t^2*diff(y(t),t$2) + t*diff(y(t),t) + (t^2-n^2)*y(t)=0;
> dsolve(deq,y(t));
> dsolve({ deq,y(0)=0,D(y)(0)=0} ,y(t),numeric);
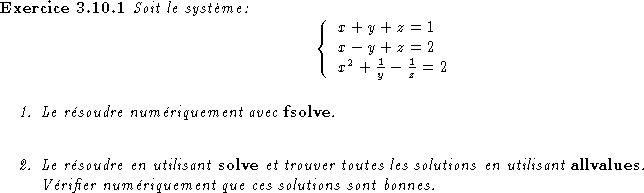
Correction:
> e1:=x+y+z=1 ;
> e2:= x-y+z=2;
> e3:= x^2+1/y-1/z=2;
> fsolve({e1,e2,e3},{x,y,z});
allvalues permet de remplacer RootOf par sa valeur si c'est possible et l'argument 'd' permet de préciser que les RootOf d'une même équation représentent la même valeur et donc de ne pas multiplier les solutions (essayer sans l'argument).
Correction:
> s:=solve({e1,e2,e3},{x,y,z});
> s:=allvalues(s,'d');
> vf:=evalf(s);
> subs(vf[1],{e1,e2,e3});
> subs(vf[2],{e1,e2,e3});
> subs(vf[3],{e1,e2,e3});