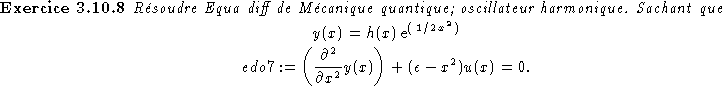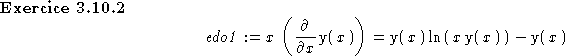
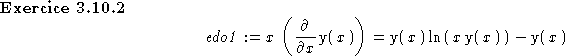
Correction:> edo1:=x*diff(y(x),x)=y(x)*ln(x*y(x))-y(x); > solimp:=dsolve(edo1,y(x)); > readlib(isolate): solexp1:=isolate(solimp,y(x)); > solexp2:=dsolve(edo1,y(x),explicit); > solexp2a:=expand(solexp2); > solexp2b:=subs(_C1=1/c,solexp2a); > verif:=subs(solexp2b,edo1);expand(lhs(verif)-rhs(verif));

Correction:
> alias(y=y(x));
> edo2:=diff(y,x)=sqrt(y^2+1);
> infolevel[dsolve]:=2;
> solimp:=dsolve(edo2,y);
> solexp1:=isolate(solimp,y);
> verif1:=subs(_C1+x=z,solexp);expand(verif);convert(",trig);simplify(");
> verif2:=subs(z=_C1+x,solexp);(eval\@subs)(verif2,edo2);simplify(");
> solexp2:=dsolve(edo2,y,explicit=true);
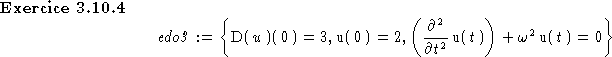
Correction:> sol:=dsolve(edo3,u(t));
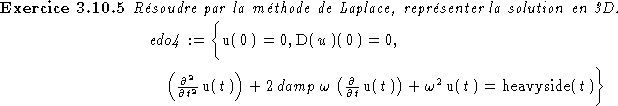
Correction:
> edo4:={diff(u(t),t$2)+2*damp*omega*diff(u(t),t)+omega^2*u(t)=heavyside(t),u(0)=0,D(u)(0)=0};
> sol1:=dsolve(edo4,u(t),laplace);
> damp:=0; sol2:=simplify(sol1);
> damp:=1/gamma; sol3:=simplify(sol1);
> plot3d(rhs(sol3),omega=2/3..4/3,t=0..20,style=hidden,orientation=[-30,45],axes=BOXED);
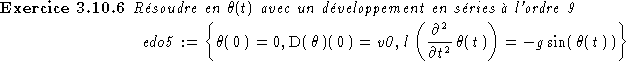
Correction:
> edo5:={l*diff(theta(t),t\$2)=-g*sin(theta(t)),theta(0)=0,D(theta)(0)=v0};
> sol:=dsolve(edo5,theta(t),method=series)
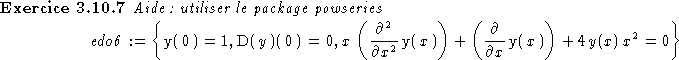
Correction:
pour Maple V.3.3
> with(powseries):
> edo6:=x*diff(y(x),x$2)+diff(y(x),x)+4*y(x)*x^2=0;
> sol:=powsolve({edo6,y(o)=1,D(y)(0)=0});
> tpsform(sol,x,15);