Calcul matriciel

• Calcul matriciel: ?linalg, with(linalg);

  > with(linalg);A:=array([[1,2],[1,3]]); b:=array([1,-2]); :
  > linsolve(A,b);
  > A:=matrix(2,2,[a11,a12,a21,a22]);

Correction:

> alias(Id=&*())
> A1:= matrix(2,2,[a,b,c,d]):A2:=toeplitz([alpha,beta]):
> A3:=matrix(3,2,(i,j)-> i+j-1):
> evalm(A1+A2);evalm(3*A1-2*A2);evalm(A1-1);whattype(");
> # Attention a * qui est different de &* 
> evalm(A1 &* 1/A1);evalm(A1 * (1/A1));evalm(A1^0));

Correction:

> toep:=matrix([[1,0,0,1],[1,0,1,1],[0,0,1,0],[0,1,1,0]]);
> trace(toep);det(toep);
> rank(A);kernel(A);rowspace(A);colspace(A);

Correction:

> with(linalg);
> mat:=matrix(5,5,(i,j)->(x.i^(j-1)));
> d:=det(mat);
> factor(d);

On ne peut pas utiliser factor sur un objet matriciel, c'est pourquoi la fonction map est nécéssaire.

> mat:=matrix(3,3,(i,j)->(x.i^(j-1)));
> i:=inverse(mat);
> map(factor,i);

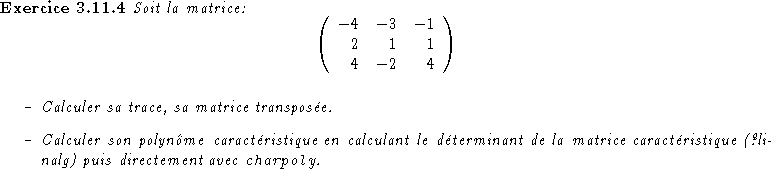
Correction:

> with(linalg):
> A:=matrix(3,3,[-4,-3,-1,2,1,1,4,-2,4]);
> trace(A);
> det(A);
> transpose(A);
> Id:= array(identity, 1..3,1..3);
> pol1:=det(A-x*Id);
> pol2:=charpoly(A,x); # = det(A-x*Id)
> matcar:=charmat(A,x); # = A-x*Id

Correction:

> B:=matrix(4,4,[16,2,3,13,5,11,10,8,9,7,6,12,4,14,15,1]);
> valprop:=eigenvals(B);

c'est un carré magique : somme des ligne et somme des colonnes sont constantes. Ce type de matrice a des valeurs propres toujours réelles.