La transformée de Fourier rapide

         

La FFT, ou transformée de Fourier rapide, est un des quelques algorithmes dont la publication a provoqué une véritable révolution dans le champ technique. Généralement associé aux noms de J.W. Cooley et J.W. Tuckey qui l'ont publié en 1965, cet algorithme de calcul de la transformée de Fourier discrète avait été maintes fois << redécouvert >> depuis Gauss, notamment par Danielson et Lanczos en 1942. La FFT permet de ramener le calcul de la transformée de Fourier discrète de à opérations ; cette réduction de complexité suffit à faire passer d'impossibles à facilement résolubles nombre de problèmes.

La transformée de Fourier discrète d'un n-uplet de nombres complexes est le n-uplet défini par

où . Notons que et que pour n=1, ceci se réduit en . La transformée inverse se calcule ainsi :

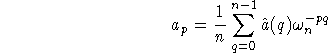
Supposons que n=2m et séparons les éléments de a d'indices pairs de ceux d'indices impairs :

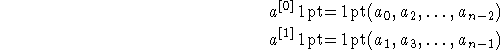
Alors, en séparant la somme en deux termes regroupant d'une part les p=2j et d'autre part les p=2j+1, et en utilisant l'égalité :

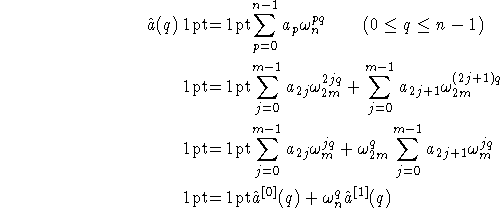
Ainsi, pour calculer la transformée de Fourier sur n points, il suffit de calculer deux transformées de Fourier sur n/2 points, de faire n multiplications et n additions. Si n est une puissance de 2, cette décomposition peut s'appliquer récursivement, ce qui donne pour équation de complexité : . Il en résulte une complexité en opérations.

  
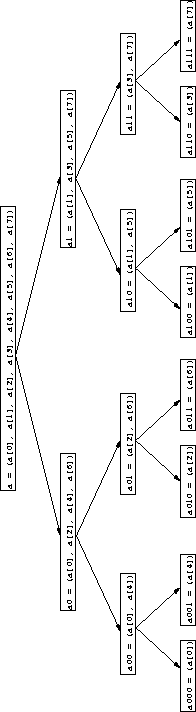
Figure: Arbre des appels de la FFT sur 8 points

La figure représente l'arbre des appels de ce calcul récursif pour n=8 points : aux feuilles, la FFT sur 1 point, qui est l'identité. L'ordre dans lequel les sont rangés dans les feuilles, de gauche à droite, est << l'inverse binaire >> de p. La fonction bit_rev(h,p) renverse la représentation binaire de n, pour ; par exemple, ; on utilise l'opérateur dyadique << (non décrit dans ce cours, comme les autres opérateurs dyadiques &, |, ^ et ~) pour calculer :

int bit_rev(int h, int p) {
  int y = 0;
  int n = 1 << h;        /* n = 2 puissance h */      
  int r;
  while (h>0) {
    h = h-1;
    n = n/2;
    r = p%2;
    p = p/2;
    if (r == 1) {
      y = n + y;
    }
  }
  return y;
}

On va donc commencer par permuter le n-uplet a pour ranger ses éléments dans cet ordre :

void bit_rev_array(int h, const int a[], int b[]) {
  int p;
  for (p=0; p < 1<<h; p++) {
    b[bit_rev(h,p)] = a[p];
  }
}

Cela va permettre de construire un algorithme itératif, qui parcourt l'arbre des feuilles vers la racine.

En utilisant la périodicité de la transformée de Fourier, et l'égalité , on peut réécrire la dernière expression de :

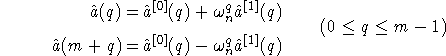
Cette transformation, de la forme , est appelée un papillon (en anglais, butterfly) ; on l'appliquera successivement avec , , , ..., .

Plutôt que de programmer cette transformation sur des nombres complexes (ce qui est légèrement plus ennuyeux), on va écrire le programme en arithmétique modulo N, où , et t est un entier quelconque, en posant , qui est une racine n-ème principale de l'unité dans ; on a toujours . Par exemple, quand t=2 et , on a N=257, et ; un n-uplet et sa transformée sont :

La fonction butterfly modulo N s'écrit :

void butterfly(int a[], int j, int k, int alpha, int N) {
  int u = a[j];
  int v = (alpha * a[k]) % N;
  a[j] = (u+v) % N;
  a[k] = (u-v+N) % N;
}

void fft(int h, int N, int omega, const int a[], int fft_a[]) {
  int n = 1<<h;
  int l;
  bit_rev_array(h, a, fft_a);
  for (l=1; l<=h; l++) {
    int i;
    int alpha = 1;
    int omega_l = expmod(omega, 1<<(h-l),N);
    int m = 1 << l;
    for (i=0; i<m/2; i++) {
      int j;
      for (j=i; j<n; j = j+m) {
        butterfly(fft_a, j, j+m/2, alpha, N);
      }
      alpha = (alpha * omega_l) % N;
    }
  }
}