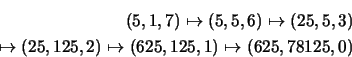Invariants : l'exponentiation

C++ ne disposant pas d'un opérateur d'exponentiation, il faut la programmer, ou bien, dans le cas des nombres flottants, utiliser celle définie dans la librairie mathématique. Le programme suivant calcule $x^e$, pour des entiers $x$ et $e$ avec $e\ge 0$, en accumulant (par multiplication) $x$ dans $y$, ceci $e$ fois, l'expression $y*x^e$ étant un invariant de boucle :

int exp(int x, int e) {
  int y = 1;

  while (e != 0) {
    y = y*x;
    e = e-1;
  }
  return y;
}

Chaque itération effectue une transformation $(y,e)\mapsto(y',e')$ ; par exemple, le calcul de exp(5,8) effectue les transformations successives suivantes de $(y,e)$ :

$$\begin{eqnarray*} (1,8) \mapsto (5,7) \mapsto (25,6) \mapsto (125,5) \mapsto (62... ... (3125,3) \mapsto (15625,2) \mapsto (78125,1) \mapsto (390625,0) \end{eqnarray*}$$

On vérifie l'invariant

$$y' x^{e'} = yxx^{e-1} = y x^e$$

On a donc l'égalité de valeur de cet invariant au début de la boucle (quand $y=1$) et à la fin de la boucle (quand $e=0$) :

$$x^{e_{\mathrm{initial}}} = y_{\mathrm{final}}$$

On notera que la version récursive équivalente à ce programme itératif n'est pas celle que l'on écrirait directement à partir de la définition par récurrence de la fonction puissance, mais est la suivante (la boucle du while modifiant les variables y et e, la fonction récursive doit prendre ces valeurs en argument) :

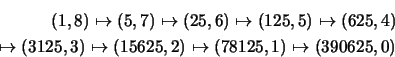
int exp_rec_aux(int x, int y, int e) {
  if (e == 0) {
    return y;
  } else {
    return exp_rec_aux(x, y*x, e-1);
  }
}

int exp_rec(int x, int e) {
  return exp_rec_aux(x,1,e);
}

La fonction exp_rec_aux est une fonction auxiliaire⁹ qui ne sera appelée que par exp_rec.

Pour les trois programmes précédents, le nombre d'itérations ou d'appels récursifs est l'entier $e$. Il est possible d'accélérer significativement ce calcul en ramenant ce nombre de $e$ à au plus $2\log_2 e$, grâce à la propriété suivante :

$$\begin{eqnarray*} x^{2e+1} &= &x * x^{2e} \\ x^{2e} &= &(x^2)^e \end{eqnarray*}$$

Par exemple, $x^{10} = (x^2)^5 = x^2 (x^2)^4 = x^2 ((x^2)^2)^2$ en quatre multiplications au lieu de 9. On obtient ainsi la définition

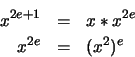
int exp_fastrec_aux(int x, int y, int e) {
  if (e == 0) {
    return y;
  } else if (e % 2 == 1) {
    return exp_fastrec_aux(x, x*y, e-1);
  } else {
    return exp_fastrec_aux(x*x, y, e/2);
  }
}

La version itérative s'écrit facilement à partir de cette version récursive terminale, en remplaçant la liste des arguments des appels récursifs par des affectations appropriées :

int exp_fastiter(int x, int e) {
  int y = 1;

  while (e!=0) {
    if (e%2 == 1) {
      y = x*y;
      e = e-1;
    } else {
      x = x*x;
      e = e/2;
    }
  }
  return y;
}

Le cas bénéficiant de la plus forte accélération est celui où l'exposant est une puissance de 2 ; voici la suite des transformations de $(x,y,e)$ pour le calcul de $5^8$ (en trois itérations au lieu de 8):

$$(5,1,8) \mapsto (25,1,4) \mapsto (625,1,2) \mapsto (390625,1,0)$$

La situation est moins favorable quand l'exposant n'est pas une puissance de 2 ; le calcul de $5^7$ se fait en 5 itérations, soit moins de $2\log_2 7$ :

$$\begin{eqnarray*} (5,1,7) \mapsto (5,5,6) \mapsto (25,5,3) \\ \mapsto (25,125,2) \mapsto (625,125,1) \mapsto (625,78125,0) \end{eqnarray*}$$

Cet algorithme est décrit dans le Chandah Sutra d'Acharya Pingala (écrit avant 200 ans avant J.C.).