Hachage par chaînage

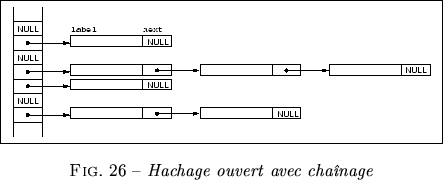
La méthode de hachage par adressage ouvert avec résolution linéaire a l'inconvénient d'effectuer des comparaisons avec plusieurs cases successives de la table, qui n'ont pourtant pas la même valeur de hachage que la chaîne recherchée. Pour éviter ces comparaisons inutiles, on va << chaîner >> les objets ayant la même valeur de hachage.

La table de hachage est implémentée par un tableau de pointeurs de list_cell et non comme un tableau d'enregistrements :

list t[N];

La recherche d'un enregistrement se fait simplement en parcourant la liste des enregistrements ayant la même valeur de hachage, à l'aide de la fonction de recherche sur les listes chaînées :

list lookup(const string& key, list t[]) {
  return search(key, t[h(key)]);
}

L'insertion d'un enregistrement d dans une table t est réalisée par la fonction suivante. On commence par appeler search. En cas d'échec, il y a allocation dynamique d'une nouvelle cellule dont les deux champs sont remplis et qui est placée en tête de la liste chaînée. En cas de succès de search, il y a remplacement de l'ancien champ info par le nouveau.

void insert(const data& d, list t[]) {
  unsigned int v = h(d.key);
  list c = search(d.key, t[v]);

  if (is_empty_list(c)) {
    t[v] = list_cons(d, t[v]);             // ajout
  } else {
    (c->label).info = d.info;              // mise à jour
  }
}

La suppression d'un enregistrement dans une table est plus délicate. Il est en effet nécessaire de déterminer la cellule précédent la cellule c contenant l'enregistrement à supprimer, par :

list presearch(const string& s, list l) {
  list c;

  if (!is_empty_list(l)) {  
    for (c = l; !is_empty_list(c->next); c = c->next) {
      if (s == c->next->key) {
        return c;
      }
    }
  }
  return NULL;
}

Le cas de la cellule de tête (qui n'a donc pas de prédécesseur) doit être traité à part. Dans tous les cas, la cellule supprimée doit être dés-allouée par la fonction delete.

void remove(const string& key, list t[]) {
  unsigned int v = h(key);
  list c = t[v];
  
  if (!is_empty_list(c)) {
    if (key == c->key) {    // si la clé est dans le cellule de tête
      t[v] = c->next;
      delete c;
    } else {                // sinon
      list d;

      c = presearch(key, c);
      d = c->next;
      c->next = c->next->next;
      delete d;
    }
  }
}

Le taux de chargement (voir §61) $\alpha = n/N$ est la longueur moyenne des listes chaînées. Sous une hypothèse d'uniformité de la fonction de hachage, on montre que le nombre moyen d'accès nécessaires pour une recherche, négative ou positive, est d'au plus $1+\alpha$.