Types abstraits et sous-typage

On souhaite à présent modéliser plusieurs classes d'objets géométriques : les points, les cercles et les rectangles. Tous ces objets ont une surface, mais la méthode de calcul de cette surface dépend de la classe de l'objet considéré. Un point du plan est défini par ses deux coordonnées, un cercle est défini par son centre et son rayon, un rectangle est défini par ses points supérieur gauche et inférieur droit. Voici par exemple la construction de deux points, d'un cercle et d'un rectangle et l'invocation d'une méthode surface() sur ces objets, en supposant que les classes correspondantes ont été définies par ailleurs, et qu'elles contiennent une méthode surface() :

class Test {
  public static void main(String[] args) {
    Point o = new Point(), p = new Point(1,1);
    Cercle c = new Cercle(o, 2);              
    Rectangle r = new Rectangle(o, p);        
    double sp = p.surface();
    double sc = c.surface();
    double sr = r.surface();
  }
}

 

Il n'y a pas de difficulté pour définir trois classes Cercle, Rectangle et Point, chacune disposant d'une méthode surface() appropriée. Voici par exemple la classe Cercle, qui comporte deux champs, un constructeur et une méthode :

class Cercle {
  Point centre;
  double rayon;
  Cercle(Point centre, double rayon) {
    this.centre = centre;
    this.rayon = rayon;
  }
  double surface() {
    return Math.PI * rayon * rayon;
  }
}

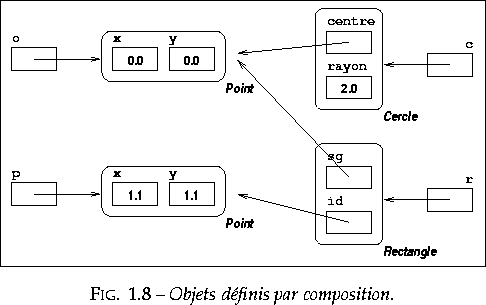
On notera au passage que la classe Cercle a un champ centre dont le type, Point est une classe. Ceci ne signifie pas qu'un objet de type Cercle contienne un objet de type Point. La valeur d'un champ est toujours une valeur, ce ne peut pas être un objet ; la valeur de centre est une référence à un objet (figure 1.8). De la même façon, la classe Rectangle a deux champs sg et id (qui désignent les sommets << supérieur gauche >> et << inférieur droit >> du rectangle) de type Point. Les instances des classes Cercle et Rectangle sont des exemples d'objets composés à partir d'autres objets (ici, des points). Il est fréquent qu'une classe soit définie par composition  à partir d'autres classes.

Supposons maintenant que l'on veuille tirer une forme au hasard, à pile ou face, puis calculer sa surface. Il semble naturel de former l'expression suivante :

  (Math.random()>0.5 ? c : r).surface();

Cependant cette expression n'est pas typée correctement parce que c et r ne sont pas du même type et aucun n'est un sous-type de l'autre. Il en est de même de l'expression Math.random()>0.5 ? true : 3, car boolean n'est pas un sous-type de int et vice-versa. La solution est d'introduire un nouveau type, Forme, dont Cercle et Rectangle seront des sous-types, de sorte que Math.random()>0.5 ? c : r soit une expression de type Forme. La classe Forme devra donc avoir une méthode surface(), puisque toute forme a une surface. Cependant, comme le calcul de la surface ne peut être fait que pour une forme particulière, la méthode surface de la classe Forme ne peut pas avoir de corps ; on dit que c'est une méthode abstraite et on la déclare en remplaçant le corps par un ';' et en faisant précéder son type de retour par le mot-clé abstract.

      Une classe qui contient au moins une méthode abstraite, comme la classe Forme, est appelée une classe abstraite. Sa définition doit aussi être précédée du mot-clé abstract :

abstract class Forme {
  abstract double surface();
}

Notons qu'on ne peut pas créer un objet d'un type abstrait : une classe abstraite n'a pas d'instance, l'expression new Forme() n'est pas correcte. Pour faire de Point, Cercle et Rectangle des sous-types de Forme, il suffit de les déclarer comme des sous-classes de Forme, au moyen du mot-clé extends  :

class Cercle extends Forme {
  Point centre;
  double rayon;
  Cercle(Point centre, double rayon) {
    this.centre = centre;
    this.rayon = rayon;
  }
  double surface() {
    return Math.PI * rayon * rayon;
  }
}

class Point extends Forme { ... }
class Rectangle extends Forme { ... }

Ces définitions font des trois types Point, Cercle, Rectangle des sous-types du type Forme. L'expression Math.random()>0.5 ? c : r est alors de type Forme et on peut lui appliquer la méthode surface(), qui est abstraite dans Forme, mais implémentée dans ses sous-types Point, Cercle et Rectangle. On dit parfois que ces trois types sont des types concrets. Ceci permet aussi de placer dans un tableau de Forme des objets de types différents :

Forme[] t = {o, c};

Plus généralement, la relation de sous-typage  permet d'utiliser une expression d'un sous-type de t dans certains contextes où une expression de type t serait attendue : dans le membre droit d'une affectation ou comme argument d'une méthode. Ceci permet d'affecter à une variable de type Forme un objet de type Cercle :

Forme c = new Cercle(new Point(), 2);

Par contre, il n'est pas possible d'affecter à une variable de type t une expression d'un sur-type de t, ou d'invoquer une méthode ou un constructeur avec un argument dont le type est un sur-type du type du paramètre correspondant :

Point q = p;          // ERREUR (à la compilation)

Une opération de transtypage est indispensable dans ce cas et conduira à une vérification, à l'exécution du fait que p désigne effectivement un objet de classe Point :

Point q = (Point)p; 

Une expression comportant un transtypage vers un sur-type est toujours correctement typée ; son exécution pourra déclencher une exception à la compilation :

Point q = (Point)r;   // correct à la compilation
                      // ERREUR à l'exécution