Types récursifs

Une classe est définie récursivement, ou est récursive si l'un de ses champs a pour type cette classe. Plus généralement, on peut définir un ensemble de types mutuellement récursifs, de façon analogue aux fonctions mutuellement récursives. Cet auto-référencement est permis précisément parce que

• la valeur du champ est une référence à un objet et non l'objet lui-même ;
• une référence peut être nulle.

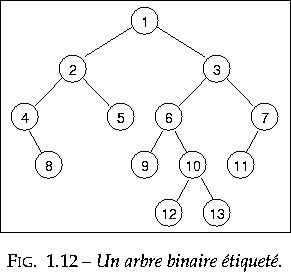
Les listes et les arbres sont des exemples classiques de types récursifs. Voici la définition (récursive) des arbres binaires étiquetés, qu'on appelera arbres par la suite : un arbre est soit l'arbre vide, soit formé d'une étiquette et de deux arbres, appelés fils gauche et fils droit. Nous supposons pour l'instant que l'étiquette est un entier. Un exemple d'arbre est représenté sur la figure 1.12.

 

Une traduction possible de cette définition mathématique en une classe est la suivante :

class ArbreBinaire {
  int étiquette;
  ArbreBinaire gauche;
  ArbreBinaire droit;
  ArbreBinaire(int étiquette, 
               ArbreBinaire gauche, 
               ArbreBinaire droit) {
    this.étiquette = étiquette;
    this.gauche = gauche;
    this.droit = droit;
  }
}

 

L'arbre vide est représenté par la valeur null, et un arbre non-vide est créé à l'aide du constructeur ArbreBinaire ; par exemple, l'arbre de la figure 1.12 peut ainsi être construit par :

  ArbreBinaire c = 
    new ArbreBinaire(1, 
      new ArbreBinaire(2, 
        new ArbreBinaire(4, 
          null, 
          new ArbreBinaire(8, null, null)),
      new ArbreBinaire(5, null, null)),
    new ArbreBinaire(3,
      new ArbreBinaire(6,
        new ArbreBinaire(9, null, null),
        new ArbreBinaire(10,
          new ArbreBinaire(12, null, null),
          new ArbreBinaire(13, null, null))),
      new ArbreBinaire(7,
        new ArbreBinaire(11, null, null),
        null)));

Cette représentation des arbres est correcte et commode mais a un défaut : l'arbre vide n'est pas un objet. Par suite, on ne peut pas définir de méthode d'instance pour tester le fait qu'un arbre soit vide. On ne peut que recourir au test d'égalité à null. L'utilisation d'un type abstrait permettra d'y remédier.