L'analyse quantitative de l'information est due à Shannon (1948). Il définit, dans un cadre probabiliste, une notion d'entropie, terme dû à Clausius (1864), qui a des interprétations diverses en informatique, en thermodynamique et en probabilités, pourtant toutes liées par des intuitions communes.
Considérons une partition
![]() d'un espace
de probabilités
d'un espace
de probabilités
![]() en un ensemble
d'événements :
en un ensemble
d'événements :
![]() ,
avec
,
avec
![]() si
si
![]() .
En posant
pi=P(Ei), et en
utilisant le logarithme en base 2 (par convention,
.
En posant
pi=P(Ei), et en
utilisant le logarithme en base 2 (par convention,
![]() ),
l'entropie de
),
l'entropie de
![]() est définie par :
est définie par :
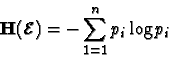
Dans les applications au codage, ![]() est l'alphabet source, et
chaque événement est un symbole de l'alphabet. Les probabilités pis'obtiennent généralement par la mesure de la fréquence des
symboles dans des textes usuels.
est l'alphabet source, et
chaque événement est un symbole de l'alphabet. Les probabilités pis'obtiennent généralement par la mesure de la fréquence des
symboles dans des textes usuels.
L'entropie mesure l'information par l'incertitude qu'elle permet de
lever : incertitude avant, information après la réception
d'un message identifiant l'un des événements de
![]() .
Elle
est ainsi maximale quand tous les événements sont équiprobables,
c'est-à-dire pi = 1/n :
.
Elle
est ainsi maximale quand tous les événements sont équiprobables,
c'est-à-dire pi = 1/n :
![]() .
On
retrouve ainsi le nombre de bits nécessaires pour coder un élément d'un
ensemble de cardinal n, en l'absence d'hypothèse probabiliste. Par
exemple, pour les 26 lettres de l'alphabet, il faut au moins
.
On
retrouve ainsi le nombre de bits nécessaires pour coder un élément d'un
ensemble de cardinal n, en l'absence d'hypothèse probabiliste. Par
exemple, pour les 26 lettres de l'alphabet, il faut au moins
![]() bits (on doit donc en utiliser 5). L'entropie est minimale, et
nulle, quand un des événements est de probabilité 1 : il n'y a aucune
incertitude, et il est inutile de coder des événements de probabilité
nulle. Un message codé sur zéro bit suffit à porter une information sûre
!
bits (on doit donc en utiliser 5). L'entropie est minimale, et
nulle, quand un des événements est de probabilité 1 : il n'y a aucune
incertitude, et il est inutile de coder des événements de probabilité
nulle. Un message codé sur zéro bit suffit à porter une information sûre
!
Dans les cas intermédiaires, entre 0 et ![]() ,
le rapport
,
le rapport
![]() mesure le taux de compression
idéal que l'on obtiendrait en ne codant que les messages << les plus
fréquents >>, et
mesure le taux de compression
idéal que l'on obtiendrait en ne codant que les messages << les plus
fréquents >>, et ![]() mesure la redondance intrinsèque, en terme
d'information, d'un code représentant tous les messages possibles.
Cette redondance est utile car elle permet de décrypter des messages
chiffrés alors que la clé de déchiffrement est inconnue, et de façon
plus courante, de corriger des fautes d'orthographe. La compression de
données, requise pour réduire le coût des supports de stockage et de
transmission de l'information, cherche au contraire à diminuer cette
redondance.
mesure la redondance intrinsèque, en terme
d'information, d'un code représentant tous les messages possibles.
Cette redondance est utile car elle permet de décrypter des messages
chiffrés alors que la clé de déchiffrement est inconnue, et de façon
plus courante, de corriger des fautes d'orthographe. La compression de
données, requise pour réduire le coût des supports de stockage et de
transmission de l'information, cherche au contraire à diminuer cette
redondance.
On peut montrer que la longueur moyenne minimale, L, d'un codage
binaire de l'alphabet source vérifie :