code de Huffman pour l'alphabet source
Quand il s'agit de transmettre de l'information sur un canal non bruité, l'objectif prioritaire est de minimiser la taille de la représentation de l'information : c'est le problème de la compression de données. Le code de Huffman (1952) est un code de longueur variable optimal, c'est-à-dire tel que la longueur moyenne d'un texte codé soit minimale. On observe ainsi des réductions de taille de l'ordre de 20 à 90%. Ce code est largement utilisé, souvent combiné avec d'autres méthodes de compression.
L'algorithme de Huffman met en ![]() uvre plusieurs structures de
données. Il opère sur une forêt , c'est-à-dire un
ensemble d'arbres. Ceux-ci sont plus précisément des arbres binaires
pondérés . Tout n
uvre plusieurs structures de
données. Il opère sur une forêt , c'est-à-dire un
ensemble d'arbres. Ceux-ci sont plus précisément des arbres binaires
pondérés . Tout n![]() ud est affecté d'un poids,
qui est la somme des poids de ses enfants ; le poids de l'arbre est, par
définition, le poids de sa racine. La forêt initiale est formée d'un
arbre à un n
ud est affecté d'un poids,
qui est la somme des poids de ses enfants ; le poids de l'arbre est, par
définition, le poids de sa racine. La forêt initiale est formée d'un
arbre à un n![]() ud pour chaque symbole de l'alphabet source, dont le
poids est la probabilité d'occurence de ce symbole. La forêt finale est
formée d'un unique arbre, de poids 1, qui est l'arbre de décodage du
code. L'algorithme est de type glouton
: il choisit à chaque étape les deux arbres de poids minimaux, soit
a1 et a2, et les remplace par l'arbre binaire pondéré d'enfants
a1 et a2 (ayant donc comme poids la somme du poids de a1 et du
poids de a2). La structure de données contenant les arbres doit
permettre les opérations suivantes : déterminer l'arbre de poids minimum
et l'extraire de la forêt, insérer un arbre dans la forêt. La
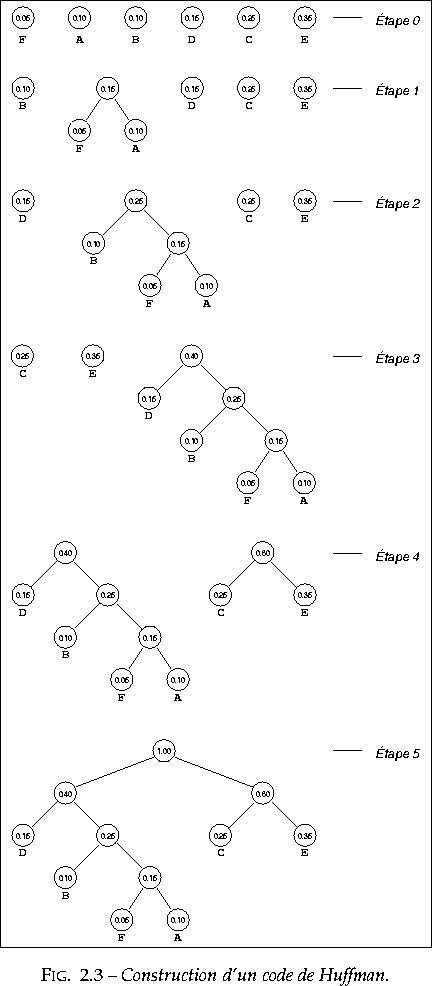
figure 2.3 représente les étapes de la construction d'un
ud pour chaque symbole de l'alphabet source, dont le
poids est la probabilité d'occurence de ce symbole. La forêt finale est
formée d'un unique arbre, de poids 1, qui est l'arbre de décodage du
code. L'algorithme est de type glouton
: il choisit à chaque étape les deux arbres de poids minimaux, soit
a1 et a2, et les remplace par l'arbre binaire pondéré d'enfants
a1 et a2 (ayant donc comme poids la somme du poids de a1 et du
poids de a2). La structure de données contenant les arbres doit
permettre les opérations suivantes : déterminer l'arbre de poids minimum
et l'extraire de la forêt, insérer un arbre dans la forêt. La
figure 2.3 représente les étapes de la construction d'un

code de Huffman pour l'alphabet source
![]() ,
avec les
probabilités
P(A) = 0,10,
P(B) =
0,10,
P(C) = 0,25,
P(D) = 0,15,
P(E) = 0,35,
P(F) = 0,05. Si
l'on utilise les bonnes structures de données pour représenter les
arbres et les forêts (par exemple, une file de priorité ), le coût de la construction du code est en
,
avec les
probabilités
P(A) = 0,10,
P(B) =
0,10,
P(C) = 0,25,
P(D) = 0,15,
P(E) = 0,35,
P(F) = 0,05. Si
l'on utilise les bonnes structures de données pour représenter les
arbres et les forêts (par exemple, une file de priorité ), le coût de la construction du code est en
![]() pour un alphabet à n symboles. Le code d'un symbole est alors
déterminé en suivant le chemin depuis la racine de l'arbre jusqu'à la
feuille associée à ce symbole en concaténant successivement un
0 ou un 1 selon que la branche suivie est à gauche ou
à droite.
pour un alphabet à n symboles. Le code d'un symbole est alors
déterminé en suivant le chemin depuis la racine de l'arbre jusqu'à la
feuille associée à ce symbole en concaténant successivement un
0 ou un 1 selon que la branche suivie est à gauche ou
à droite.
Le codage se réalise facilement à l'aide d'une table associant à chaque
symbole son code ; une fois ce code construit, le décodage se réalise
avec un arbre de décodage (figure 2.2,
page ![]() ), grâce à la propriété de préfixe des
codes de Huffman.
), grâce à la propriété de préfixe des
codes de Huffman.
| symbole | code |
| A | 0111 |
| B | 010 |
| C | 10 |
| D | 00 |
| E | 11 |
| F | 0110 |
Notons que si l'on utilisait un code binaire de longueur constante,
trois bits seraient nécessaires (car l'alphabet-source a 6 symboles, et
![]() ). Compte tenu de ces probabilités, le code obtenu a
une longueur moyenne de 2,4, ce qui représente une compression de
). Compte tenu de ces probabilités, le code obtenu a
une longueur moyenne de 2,4, ce qui représente une compression de
![]() par rapport à un codage de longueur constante minimum ; par
rapport à un codage standard de chaque symbole sur un octet, la
compression est de
par rapport à un codage de longueur constante minimum ; par
rapport à un codage standard de chaque symbole sur un octet, la
compression est de ![]() .
Peut-on faire mieux ? La réponse à cette
question relève de la théorie de l'information, branche commune à
l'informatique et au calcul des probabilités (la réponse est oui, mais
pas beaucoup mieux : la longueur moyenne minimale d'un code pour ce
langage est 2,32).
.
Peut-on faire mieux ? La réponse à cette
question relève de la théorie de l'information, branche commune à
l'informatique et au calcul des probabilités (la réponse est oui, mais
pas beaucoup mieux : la longueur moyenne minimale d'un code pour ce
langage est 2,32).