




Next: Codes
Up: No Title
Previous: La Machine Virtuelle Java
Le premier [précepte] était de ne recevoir jamais aucune chose pour
vraie que je ne la connusse évidemment être telle; c'est-à-dire,
d'éviter soigneusement la précipitation et la prévention, et de ne
comprendre rien de plus en mes jugements que ce qui se présenterait
si clairement et si distinctement à mon esprit, que je n'eusse
aucune occasion de le mettre en doute.
Le second, de diviser chacune des difficultés que j'examinerais, en
autant de parcelles qu'il se pourrait, et qu'il serait requis pour
les mieux résoudre.
Le troisième, de conduire par ordre mes pensées, en commençant par
les objets les plus simples et les plus aisés à connaître, pour
monter peu à peu comme par degrés jusques à la connaissance des plus
composés, et supposant même de l'ordre entre ceux qui ne se
précèdent point naturellement les uns les autres.
Et le dernier, de faire partout des dénombrements si entiers et des
revues si générales, que je fusse assuré de ne rien omettre.
Descartes
Le mot algorithme provient du nom d'un mathématicien persan du IXe
siècle, Mohammed ibn-Musa al-Khuwarizmi, dont le livre d'arithmétique,
utilisant la numération arabe et des règles de calcul, montra
l'inutilité des tables et abaques. Autant dire que les algorithmes, au
sens de solution algorithmique à des problèmes, sont connus et
utilisés bien avant les débuts de l'informatique. La notion actuelle
d'algorithme a été élaborée par les logiciens des années 1930
(Herbrand, Gödel, Church et Turing), eux-mêmes précurseurs de
l'informatique.
L'algorithmique est la branche de l'informatique qui traite des
algorithmes. On peut voir cette branche comme l'économie de
l'informatique, ou comment mettre en 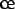 uvre des ressources de
calcul pour résoudre des problèmes au moindre coût. Comment évaluer ce
coût ? Le temps d'exécution d'un programme peut être mesuré
expérimentalement. Sous Linux, la commande time affiche
plusieurs estimations de ce temps, en secondes ; par exemple, la
commande java Simulation 1000000 est exécutée et son temps
d'exécution est évalué en soumettant la commande suivante au shell :
uvre des ressources de
calcul pour résoudre des problèmes au moindre coût. Comment évaluer ce
coût ? Le temps d'exécution d'un programme peut être mesuré
expérimentalement. Sous Linux, la commande time affiche
plusieurs estimations de ce temps, en secondes ; par exemple, la
commande java Simulation 1000000 est exécutée et son temps
d'exécution est évalué en soumettant la commande suivante au shell :
linux% time java Simulation 1000000
13.240u 0.870s 0:19.30 73.1% 0+853k 0+16io 0pf+0w
- le premier nombre (suffixé par u, pour user) est
le temps d'exécution des instructions du programme ;
- le second (suffixé par s, pour system) est le
temps d'exécution d'instructions du système nécessaires à l'exécution
du programme, mais qui ne figurent pas dans le programme ;
- le troisième est le temps écoulé entre le début et la fin de
l'exécution du programme ; ce temps pourrait être mesuré par un
utilisateur muni d'un chronomètre ; il dépend non seulement du
programme, mais aussi de la charge du système, due notamment aux autres
programmes en cours d'exécution ;
- le suivant est le pourcentage du temps consacré au programme,
c'est-à-dire
u + s rapporté au temps écoulé ;
- les trois derniers nombres sont des évaluations des accès à la
mémoire (espace utilisé, entrées-sorties, pages).
Il est important d'être capable d'évaluer a priori ce temps u,
sans devoir exécuter le programme. Si l'on dispose d'information sur la
machine, on a l'estimation suivante :
Le ou la programmeur-e peut seulement agir sur le nombre d'instructions ; les
deux autres facteurs de cette formule sont respectivement du ressort de
l'architecte de la machine et de l'électronicien. Les instructions
mentionnées dans cette formule ne sont pas celles du langage source,
mais celles de la machine ; en outre, il y a des instructions exécutées
qui ne proviennent pas du programme source (par exemple, des opérations
de récupération de la mémoire inutilisée). Cependant, une estimation du
temps d'exécution peut être obtenue en analysant le programme source.
L'usage est de dénombrer certaines instructions significatives : nombre
d'opérations arithmétiques dans un algorithme numérique, nombre
d'itérations ou d'invocations récursives, nombre de comparaisons dans un
algorithme de recherche d'un élément dans une table. Cette évaluation se
fait en fonction d'une grandeur caractéristique du problème : valeur
d'une donnée, taille d'un tableau, profondeur d'un arbre, etc. Plutôt
que de temps d'exécution, on parlera d'une
mesure de complexité. En outre, il s'agit souvent de comparer
plusieurs algorithmes entre eux, indépendamment des machines auxquelles
ils sont destinés. On s'intéresse donc surtout à l'ordre de grandeur
d'une mesure de complexité, c'est-à-dire à des estimations
asymptotiques. On rencontrera notamment des algorithmes
linéaires quand la complexité est en 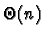 ,
logarithmiques, en
,
logarithmiques, en
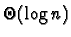 ,
quadratiques, en
,
quadratiques, en
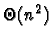 ,
etc. Rappelons que
,
etc. Rappelons que 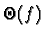 est l'ensemble des fonctions g pour lesquelles il existe des entiers
N, a et b positifs tels que
est l'ensemble des fonctions g pour lesquelles il existe des entiers
N, a et b positifs tels que
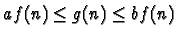 pour tout
pour tout
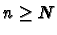 .
.





Next: Codes
Up: No Title
Previous: La Machine Virtuelle Java
R. Lalement
2000-10-23
![]() uvre des ressources de
calcul pour résoudre des problèmes au moindre coût. Comment évaluer ce
coût ? Le temps d'exécution d'un programme peut être mesuré
expérimentalement. Sous Linux, la commande time affiche
plusieurs estimations de ce temps, en secondes ; par exemple, la
commande java Simulation 1000000 est exécutée et son temps
d'exécution est évalué en soumettant la commande suivante au shell :
uvre des ressources de
calcul pour résoudre des problèmes au moindre coût. Comment évaluer ce
coût ? Le temps d'exécution d'un programme peut être mesuré
expérimentalement. Sous Linux, la commande time affiche
plusieurs estimations de ce temps, en secondes ; par exemple, la
commande java Simulation 1000000 est exécutée et son temps
d'exécution est évalué en soumettant la commande suivante au shell :
