Ordonnancement de projet

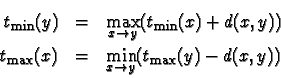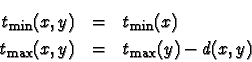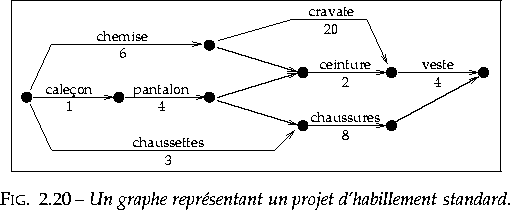
Certains problèmes d'ordonnancement de projet sont représentables à l'aide d'un graphe dont les sommets sont des événements et les arcs des tâches, ceux-ci étant étiquetés par leur durée ; le sommet initial et final d'un arc représente, respectivement, l'événement de début et de fin d'exécution de la tâche (figure 2.20). On cherche à déterminer les tâches critiques, c'est-à-dire celles dont un retard est répercuté sur l'ensemble du projet. Ce problème revient à trouver dse chemins les plus longs dans un graphe.

 

On modélise un projet par un graphe $\mathcal{G} = (S, A)$ et une fonction de durée $d:A\to\mathbf{N}$. On suppose qu'un sommet initial s et un sommet final t ont été désignés. La longueur d'un chemin est la somme des durées des arcs le composant. Un chemin critique est un chemin de s à t de longueur maximale. S'il n'existe pas de chemin critique, le projet n'est pas réalisable. Le temps minimal requis pour l'exécution d'un projet réalisable est égal à la longueur d'un chemin critique ; c'est la durée du projet. Les tâches figurant sur un chemin critique sont aussi appelées critiques, ce qui s'explique par le fait que tout retard d'exécution d'une tâche critique retarde d'autant l'exécution du projet.

Une exécution du projet est définie par une fonction de date de début d'exécution des tâches $t:A\to\mathbf{N}$. Si le projet est réalisable, on définit l'exécution au plus tôt, $t_{\min}$, et l'exécution au plus tard, $t_{\max}$ : $t_{\min}(x,y)$ est la longueur maximale des chemins de s à x (elle ne dépend pas de y), $t_{\max}(x,y)$ est la date la plus tardive pour commencer la tâche (x,y) telle que la durée totale de l'exécution soit la durée du projet. On notera qu'une tâche (x,y) est critique si $t_{\min}(x,y) = t_{\max}(x,y)$. Il est plus simple de calculer des fonctions $t_{\min}, t_{\max} : S\to\mathbf{N}$ définies par :

$$\begin{eqnarray*}t_{\min}(y) &= &\max_{x\to y} (t_{\min}(x) + d(x,y)) \\ t_{\max}(x) &= &\min_{x\to y} (t_{\max}(y) - d(x,y)) \end{eqnarray*}$$

Ces fonctions sur les sommets sont reliées aux fonctions sur les arcs de la façon suivante :

$$\begin{eqnarray*}t_{\min}(x,y) &= &t_{\min}(x) \\ t_{\max}(x,y) &= &t_{\max}(y)-d(x,y) \end{eqnarray*}$$

L'algorithme consiste en un double parcours du graphe. Dans une première phase, on calcule les dates $t_{\min}(x))$, initialisées à 0, à partir du sommet initial s, en procédant par un tri topologique du graphe (voir § 2.14, p. ). Dans une seconde phase, les $t_{\max}(x)$ sont calculées à partir du sommet final, en l'initialisant à l'aide de $t_{\min}(t)$ (la durée du projet, maintenant connue), par un tri topologique en ordre inverse. Ceci permet de déterminer si le projet est réalisable et dans le cas positif, effectuer le calcul de sa durée, des dates au plus tôt et au plus tard, et dire quelles sont les tâches critiques (figure 2.21).