L'algorithme de Floyd

Un exemple simple de programmation dynamique, mais classique, est celui du calcul des plus courts chemins dans un graphe, par l'algorithme de Floyd (1962) ; on doit plutôt parler de chemins à moindre coût, ce problème n'ayant aucune signification métrique.

   

Représentons un graphe à N sommets comme un tableau c d'entiers positifs de taille $N\times N$ ; l'élément c_ij est le coût de l'arc $i\to j$ ; si l'arc n'existe pas, on pose $c_{ij} = \infty$, de sorte qu'on travaille avec un graphe complet. Le coût d'un chemin est la somme des coûts des arcs de ce chemin. Considérons un chemin de coût minimal entre i et j et $k\not=i,j$ un sommet intermédiaire sur ce chemin : les sous-chemins de ce chemin, de i à k et de k à j sont aussi de coût minimal (sinon, en remplaçant un de ces sous-chemins par un chemin de moindre coût de mêmes extrémités, on diminuerait le coût du chemin de i à j, ce qui est impossible). Ce problème satisfait donc au principe d'optimalité.

 

L'algorithme de Floyd est une méthode ascendante, qui calcule successivement pour k croissant de 1 à N, pour tous les couples de sommets i, j, les chemins minimaux de i à j parmi ceux dont les sommets intermédiaires sont dans $\{1,\ldots, k\}$, chemins appelés les k-chemins. Notons d_ij^k le coût d'un chemin de i à j minimal parmi les k-chemins. On doit calculer d_ijⁿ à partir de d_ij⁰ = c_ij. Considérons un k-chemin de coût minimum. S'il ne contient pas k, c'est un (k-1)-chemin de coût minimum ; s'il contient k, on peut le diviser en deux sous-chemins de i à k et de k à j, qui sont eux-mêmes des k-1-chemins, et par le principe d'optimalité, chacun de ces sous-chemins est un (k-1)-chemin de coût minimal ; comme l'un des deux cas se produit, on a la relation :

$$d_{ij}^k = \min(d_{ij}^{k-1}, d_{ik}^{k-1} + d_{kj}^{k-1}).$$

Voici sur l'exemple de la figure 2.19, les matrices d^ksuccessives, calculées d'après cette relation (on a utilisé $\infty$ pour indiquer la non-existence d'un arc):

$$d^0 = \left( \begin{array}{rrrrr} 0 &3 &8 &\infty &-4 \\ \in... ...&-5 &0 &-2 \\ \infty &\infty &\infty &6 &0 \end{array}\right)$$

$$d^2 = \left( \begin{array}{rrrrr} 0 &3 &8 &4 &-4 \\ \infty &... ...&-5 &0 &-2 \\ \infty &\infty &\infty &6 &0 \end{array}\right)$$

$$d^4 = \left( \begin{array}{rrrrr} 0 &3 &-1 &4 &-4 \\ 3 &0 &-... ...5 &3 \\ 2 &-1 &-5 &0 &-2 \\ 8 &5 &1 &6 &0 \end{array}\right)$$

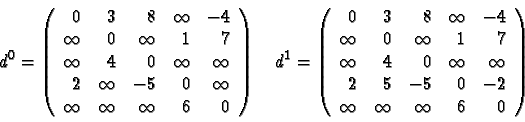
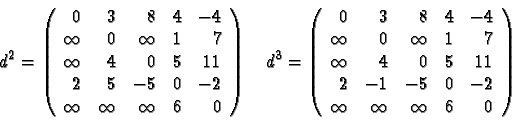
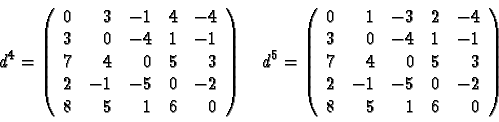
On peut interpréter cette formule récurrente comme une fonction récursive en i,j,k ; une exécution récursive conduirait à des invocations multiples, comme dans le cas de la définition récursive de la suite de Fibonacci. L'algorithme de Floyd procède au contraire par une évaluation ascendante. On l'appliquera par exemple à c pour calculer les coûts minimaux dans d:

  static final int M = Integer.MAX_VALUE;
  
  int[][] c = {
    {0, 3, 8, M, -4},
    {M, 0, M, 1, 7},
    {M, 4, 0, M, M},
    {2, M, -5, 0, M},
    {M, M, M, 6, 0}
  };

La fonction floyd() implémente cet algorithme :

  static int[][] floyd(int[][] c) {
    int n = c.length;
    int[][] d = new int[n][n];
    for (int i=0; i<n; i++) {
      for (int j=0; j<n; j++) {
        d[i][j] = c[i][j];
        }
    }
    for (int k=0; k<n; k++) {
      for (int i=0; i<n; i++) {
        for (int j=0; j<n; j++) {
          int dik = d[i][k], dkj = d[k][j];
          if (dik == M || dkj == M) continue;
          int u = dik + dkj;
          if (u < d[i][j]) {
            d[i][j] = u;
          }
        }
      }
    }
    return d;
  }

Il est facile de modifier cet algorithme pour être capable de construire les chemins minimaux : il suffit de conserver dans un autre tableau p le prédecesseur de j dans un k-chemin de coût minimal et d'ajouter l'affectation p[i][j] = p[k][j] juste après d[i][j] = u. Initialement, p_ij = i, si $i\not= j$ et $c_{ij}<\infty$, et une fois l'algorithme terminé, un chemin de coût minimal de i à j est un chemin de coût minimal de i à p_ij, suivi de l'arc $p_{ij}\to j$.