Réseaux de transport

Certains problèmes de transport (de marchandises, de fluides, d'énergie, etc) dans un réseau (routier, de distribution, etc) sont représentables de façon naturelle par des graphes dont les sommets sont des points de passage (sans stockage) et les arcs des trajets entre ces points. Le problème consiste à maximiser l'utilisation de tels réseaux, c'est-à-dire à calculer la quantité maximale transportable compte tenu des contraintes. Ce problème a bien d'autres réalisations, par exemple pour déterminer un appariement maximum dans un graphe biparti.

On modélise un réseau  de transport à l'aide d'un graphe $\mathcal{G} = (S, A)$, muni d'une fonction de capacité $c : S\times S \to \mathbf{N}$, telle que c(x,y)=0 si $(x,y)\notin A$. On suppose qu'un sommet source s et un sommet puits t ont été désignés (figure 2.22).

 

On appelle flot une fonction $f:S\times S \to\mathbf{Z}$ telle que (contraintes de capacité et de conservation, Cf. les lois de Kirchhoff) :

1.

quels que soient x, $y\in S$, $f(x,y)\le c(x,y)$

2.

quels que soient x, $y\in S$, f(x,y) = -f(y,x)

3.

quel que soit $x\neq s, t$, $\sum_{y\in S}f(x,y) = 0$

Un flot est représenté sur la figure 2.23 par la notation f(x,y) / c(x,y) en étiquette des arcs. La valeur du flot fest le nombre $\vert f\vert = \sum_{y\in S} f(s,y)$, qui est aussi égal à $\sum_{x\in S} f(x,t)$ ; elle mesure la quantité totale transportée par le flot depuis la source vers le puits. Un arc est saturé par le flot s'il est utilisé au maximum de sa capacité, c'est-à-dire si f(x,y) = c(x,y).

 

Le problème est de déterminer un flot de valeur maximale. Sa résolution fait appel à la notion de réseau résiduel d'un flot. Étant donné un réseau de graphe $\mathcal{G} = (S, A)$ et de capacité c et un flot f, on définit c_f(x,y) = c(x,y) - f(x,y), pour $(x,y)\in S\times S$; le réseau résiduel de f est défini par le graphe $\mathcal{G}_f = (S, A_f)$ dont l'ensemble des arcs est $A_f = \{(x,y)\in S\times S ; c_f(x,y)>0\}$, et par la capacité c_f(figure 2.24) ; on notera que A_f n'est pas nécessairement inclus dans A, car il peut contenir aussi l'arc réciproque d'un arc de A.

 

Un chemin d'augmentation de f dans un réseau est un chemin simple (c'est-à-dire sans boucle) de s vers t dans le graphe résiduel $\mathcal{G}_f$. La capacité d'un chemin p est la quantité c(p) maximale transportable le long de p, soit $c(p) = \min \{c_f(x,y) ; (x,y) \in p \}$. Un chemin d'augmentation permet d'augmenter f en définissant le flot noté f+p(figure 2.25) :

$$\begin{eqnarray*}(f+p)(x,y) &= &f(x,y) + c(p) \quad\mbox{si } (x,y)\in p\\ (f+p... ...\mbox{si } (y,x)\in p\\ (f+p)(x,y) &= &f(x,y) \quad\mbox{sinon} \end{eqnarray*}$$

Il s'agit bien d'un flot et c'est une augmentation de f au sens où |f+p|>|f|.

 

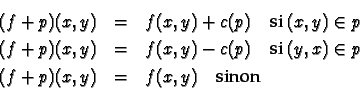
On montre alors qu'un flot est maximal si et seulement si son graphe résiduel ne contient aucun chemin d'augmentation. L'algorithme de Ford-Fulkerson (1956) consiste à augmenter le flot selon un chemin d'augmentation s'il en existe :

   

• le flot f est initialisé à 0 ;
• (itération) tant qu'il existe un chemin d'augmentation dans $\mathcal{G}_f$, en choisir un de longueur (nombre d'arcs) minimum, p (cette recherche se fait par un parcours en largeur), augmenter f selon p, puis calculer le nouveau graphe résiduel $\mathcal{G}_f$ ;
• s'il n'existe pas de chemin d'augmentation dans $\mathcal{G}_f$, alors f est un flot de valeur maximale.

Il faut choisir une structure de données adéquate ; on notera que les graphes résiduels partagent le même ensemble de sommets, mais que l'ensemble des arcs est variable. Correctement implémenté, cet algorithme a une complexité en O(|S| |A|²).