.' et la lettre Y,
plus rare, par `-.--' : c'est un exemple de code de
longueur variable, ce qui permet de représenter les lettres les
plus fréquentes par des mots plus courts. Une propriété importante est
l'unicité du décodage, problème qui ne se pose pas pour les codes de
longueur constante. Il peut être résolu, mais de façon trop coûteuse,
quand un symbole spécial sépare deux mots successifs du code (le blanc
dans le cas du Morse). On peut ne pas recourir à cette technique si
aucun mot du code n'est le préfixe d'un autre mot du code (par exemple
01 étant préfixe de 0111, ces deux mots ne peuvent
appartenir simultanément à un code préfixe) ; un code présentant cette
propriété est appelé un code préfixe . Un
exemple de tel code, dans la vie courante, est l'ensemble des numéros de
téléphone : que le 18 soit le numéro d'appel des pompiers implique
qu'aucun autre numéro ne commence par 18. En informatique, un exemple de
code de longueur variable préfixe est le code UTF-8, qui permet de
représenter les caractères Unicode sous forme d'un nombre variable
d'octets (de 1 à 3) :
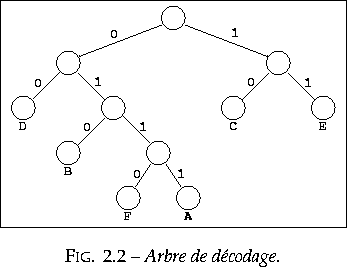
Le décodage d'un code préfixe se fait à l'aide d'une autre structure de données, un arbre, tel que celui de la figure 2.2. Il suffit de lire les symboles successifs du texte codé : si c'est un 0, on suit la branche de gauche, si c'est un 1, celle de droite ; quand on arrive à une feuille de l'arbre, on a décodé une lettre de l'alphabet source ; on remonte alors à la racine et on continue avec le symbole binaire suivant. Ainsi, avec l'arbre de la figure 2.2, 010011110 se décode en BAC, sans qu'il soit nécessaire de le décomposer a priori en 010 / 0111 / 10.
Nous présenterons trois algorithmes de codage : le codage de Huffman, pour la compression, le codage RSA, pour la confidentialité et le codage de Hamming, pour la correction d'erreurs.