Correction d'erreurs : le code Hamming

Un code correcteur d'erreur est utilisé pour transmettre un message dans un canal bruité ; il permet de reconstituer le message émis même si des erreurs (en nombre limité), dues au bruit, ont altéré le message. L'alphabet source, comme l'alphabet du code, est $\{0,1\}$. On s'intéresse au codage par blocs : chaque mot de longueur m est codé par un mot de longueur n avec $n\ge m$. Le codage est donc une application de $\{0,1\}^m$ vers $\{0,1\}^n$. Parmi les n bits du mot-code que nous allons décrire, m reproduisent le mot-source, les n-m autres sont les bits de correction : le taux de transmission est de n/m. On montre que si deux mots distincts du code diffèrent au moins en d bits, alors le code permet de corriger exactement $\frac{d-1}{2}$ erreurs.

Les codes de Hamming, pour lesquels n=2^k-1 et m=n-k, permettent de corriger une erreur ; pour k fixé et n grand, le taux de transmission est voisin de 1. Leur description fait appel à l'algèbre linéaire modulo 2, ou bien aux polynômes modulo 2. Un mot de p bits est représenté par un vecteur binaire de longueur p, c'est-à-dire un élément de l'espace vectoriel (Z/2Z)^p, par exemple pour 110 :

$$\left( \begin{array}{c} 1 \\ 1 \\ 0 \end{array}\right)$$

La matrice de parité d'un code de Hamming est une matrice binaire à klignes et n colonnes : les colonnes contiennent les représentations binaires des entiers entre 1 et n, par exemple :

$$H = \left( \begin{array}{ccccccc} 1 &0 &0 &1 &0 &1 &1 \\ 0 &1 &0 &1 &1 &1 &0 \\ 0 &0 &1 &0 &1 &1 &1 \end{array}\right)$$

La matrice de parité, H, permet de définir les mots du code : ce sont les vecteurs c de dimension n tels que Hc=0. Comme cette équation définit un sous-espace vectoriel de (Z/2Z)ⁿ, on dit qu'il s'agit d'une code linéaire ; ce sous-espace est de dimension n. Supposons que l'on reçoive c' qui diffère d'un mot du code c de un bit : c' = c+e, où e est le vecteur d'erreur, par exemple 0100000. Comme Hc=0, on a Hc'=He ; puisque e contient un seul bit (par exemple e = 0100000), le calcul de Hc' donne l'une des colonnes de H ; si on obtient Hc' = 010, ce qui est la deuxième colonne de H, c'est que l'erreur est sur le deuxième bit, c'est-à-dire e = 0100000. La correction est donc très facile. Il reste à dire comment le codage et le décodage s'effectuent, autrement dit quels sont les bits d'information et les bits de correction dans un mot du code.

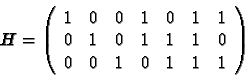
La détermination d'une base du sous-espace d'équation Hc=0 permet de formuler le codage : si G est la matrice $m\times n$ dont les lignes sont les vecteurs d'une telle base, Hc=0 équivaut à c=aG pour a, un vecteur-ligne de longueur m. Ainsi a est codé par c=aG ; on dit que G est la matrice génératrice du code.

Dans l'exemple précédent, on trouve facilement, par exemple :

$$G = \left( \begin{array}{ccccccc} 1 &1 &0 &1 &0 &0 &0\\ 0 &1... ... 1 &1 &1 &0 &0 &1 &0\\ 1 &0 &1 &0 &0 &0 &1 \end{array}\right)$$

ce qui fait que les 3 premiers bits sont ceux de correction, les 4 suivants étant les bits d'information.

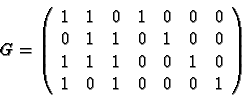
Une autre technique pour construire ce code consiste à utiliser des polynômes primitifs. On note ainsi que la matrice H s'obtient en décomposant les monômes Xⁱ, pour $i=0, \ldots, 6$ dans la base $\{ 1, X, X^2 \}$ de l'espace vectoriel des polynômes à coefficients dans Z/2Z, et modulo P=1+X+X³. On a ainsi X³ = X+1, X⁴ = X²+X, X⁵ = X²+X+1, X⁶=X²+1 modulo P (ce polynôme est primitif car les monômes forment une base de cet espace vectoriel). Par construction de H, Hb est égal à $(b_0 + \ldots + b_n X^n)$ modulo P. Il en résulte que les bits de correction sont obtenus en calculant le reste de la division euclidienne de $X^k(a_0 + \ldots + a_m X^m)$ par P. Pour le décodage, supposons qu'une erreur se soit produite sur le bit p. Au lieu de recevoir le polynôme Q, c'est Q+X^p qui est reçu. Le reste de la division euclidienne de Q+X^p par P est égal à X^p modulo P ; ceci permet de déterminer p, donc l'erreur.

Par exemple, un mot du code utilisé par le Minitel comporte 17 octets. Les 16 premiers forment un code de Hamming à 7 bits de correction : k=7, m=120 (soit 15 octets), n=127 ; le 128ème bit, dit bit de parité, est tel que le nombre de 1 dans ces 16 octets soit pair. Le 17ème octet est formé de 8 zéros ; il permet de détecter des incidents importants (par exemple, la foudre). On s'intéresse ici seulement aux 127 premiers bits. Ce code est défini, avec la méthode exposée ci-dessus, avec le polynôme P=X⁷ + X³ +1.