Pré-traitement et post-traitement

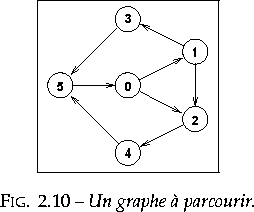
Le parcours précédent effectue en fait un traitement préfixe, où chaque sommet est traité avant ses sommets adjacents. Ceci produit une énumération préfixe des sommets, ce qui donne, dans le cas du graphe de la figure 2.10 le résultat : 0, 1, 2, 4, 5, 3. Dans l'énumération postfixe, chaque sommet est traité après tous ses sommets adjacents, soit dans cet exemple : 5, 4, 2, 3, 1, 0. Le traitement postfixe est obtenu en déplaçant l'invocation de la méthode de traitement (ici, l'impression) après le while ;

  static void parcoursProfondeur(Sommet origine, 
                                 Set sommetsVisités) {
    sommetsVisités.add(origine);
    Iterator i = origine.adjacents();
    while (i.hasNext()) { 
      Sommet suivant = (Sommet) i.next();
      if (!sommetsVisités.contains(suivant)) {
        parcoursProfondeur(suivant, sommetsVisités);
      }
    }
    System.out.println(origine.valInformation());
  }

 

Un même parcours peut comporter un pré-traitement et un post-traitement du sommet énuméré. Java ne disposant pas de variable de type fonctionnel, on doit ajouter à la méthode de parcours deux paramètres pré et post d'un type abstrait Traitement déclarant juste une méthode traite() :

package graphe;

public interface Traitement {
  void traite(Objet o);
}

La fonction de parcours en profondeur devient :

  static void parcoursProfondeur(Sommet origine, 
                                 Set sommetsVisités,
                                 Traitement pré, 
                                 Traitement post) {
    sommetsVisités.add(origine);
    pré.traite(origine);
    Iterator i = origine.adjacents();
    while (i.hasNext()) { 
      Sommet suivant = (Sommet)i.next();
      if (!sommetsVisités.contains(suivant)) {
        parcoursProfondeur(suivant, sommetsVisités, pré, post);
      }
    }
    post.traite(origine);
  }

  public static void parcoursProfondeur(Graphe g,
                                        Traitement pré, 
                                        Traitement post) {
    Iterator j = g.sommets();
    Set sommetsVisités = new HashSet();
    while (j.hasNext()) {
      Sommet s = (Sommet)j.next();
      if (!sommetsVisités.contains(s)) {
        parcoursProfondeur(s, sommetsVisités, pré, post);
      }
    }
  }

Pour l'utiliser, il faut d'abord implémenter l'interface Traitement, par exemple :

class Pre implements Traitement {
  public void traite(Object o) {
    System.out.print(o + " [");
  }
}

class Post implements Traitement {
  public void traite(Object o) {
    System.out.print("] " + o);
  }
}

Il faudra maintenant invoquer :

   Algorithmes.parcoursProfondeur(g, new Pre(), new Post())}

Notons que pour des traitements simples, une implémentation anonyme suffit (voir § 3.10). Si un seul des deux traitements est souhaité, par exemple le pré-traitement, il suffira que l'autre argument soit l'implémentation minimale suivante :

   Algorithmes.parcoursProfondeur(g, 
                                  new Pre(), 
                                  new Traitement() {
                                    public void traite(Object o) {} 
                                  });