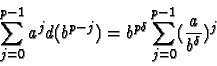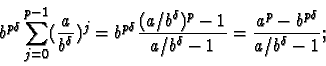Next: La transformée de Fourier
Up: Algorithmes
Previous: L'algorithme
Diviser pour régner
Un algorithme diviser pour régner a la structure suivante : pour
résoudre un problème de taille n, l'algorithme consiste à décomposer
le problème en a sous-problèmes ayant tous la taille n/b (peut-être
approximativement), à appliquer l'algorithme à tous les sous-problèmes,
puis à construire une solution du problème en composant les solutions
des sous-problèmes. Non seulement cette méthode est naturelle (et
voisine du second précepte de la méthode de Descartes), mais elle
permet souvent une réduction importante de T(n), la complexité dans le
pire des cas de l'algorithme appliqué à un problème de taille n. On
suppose que la complexité des opérations de décomposition du problème et
de recomposition des solutions des sous-problèmes a une complexité en
d(n). Enfin, on se donne la complexité T(1) sur un problème de
taille 1. La complexité de l'algorithme est donc déterminée par
l'équation de récurrence suivante :
T(n) = aT(n/b) + d(n)
Voici quelques exemples :
- recherche
dichotomique dans une table ordonnée (a=1, b=2) :
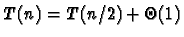 ,
d'où
,
d'où
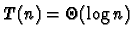 ,
alors qu'une recherche
séquentielle dans une table ordonnée est en
,
alors qu'une recherche
séquentielle dans une table ordonnée est en 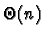 ;
;
-
tri d'une table par fusion (a=2, b=2) :
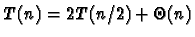 ,
d'où
,
d'où
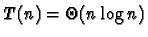 ,
alors qu'un
tri ordinaire est typiquement en
,
alors qu'un
tri ordinaire est typiquement en
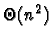 ;
;
-
transformée de Fourier rapide (a=2, b=2) :
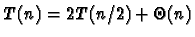 ,
d'où
,
d'où
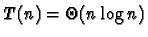 ,
alors qu'une
évaluation directe des formules est en
,
alors qu'une
évaluation directe des formules est en
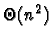 ;
;
- multiplication de deux matrices par l'algorithme de Strassen
(a=7, b=2) :
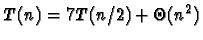 ,
d'où
,
d'où
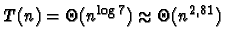 alors que la multiplication
ordinaire est en
alors que la multiplication
ordinaire est en
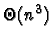 .
.
Résolvons ces équations quand n est une puissance de b ; dans ce cas
l'équation s'écrit :
T(bp) = a T(bp-1) + d(bp)
Sa solution est
Le premier terme,
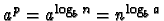 correspond à la
complexité due à la résolution de tous les sous-problèmes ; le second
terme est la complexité due à toutes les opérations de
décomposition/recomposition.
correspond à la
complexité due à la résolution de tous les sous-problèmes ; le second
terme est la complexité due à toutes les opérations de
décomposition/recomposition.
Examinons ce deuxième terme quand
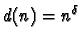 .
On a
.
On a
Discutons selon les valeurs relatives de a et 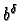 .
.
-
Si
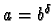 ,
cette somme vaut
,
cette somme vaut
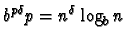 ;
donc
;
donc
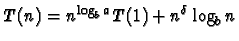 ; ainsi, si
; ainsi, si
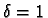 et a=b (cas très usuel, en particulier de la FFT, du tri par fusion
et du tri rapide), on a
et a=b (cas très usuel, en particulier de la FFT, du tri par fusion
et du tri rapide), on a
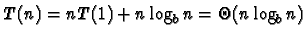 .
Si
.
Si
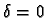 et a=1 (cas de la recherche dichotomique), on
obtient
et a=1 (cas de la recherche dichotomique), on
obtient
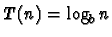 ;
;
-
Si
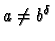 ,
,
- Si
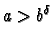 ,
le terme dominant est
,
le terme dominant est
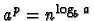 ,
qui
est indépendant de
,
qui
est indépendant de 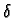 et qui est du même ordre que le premier
terme, donc
et qui est du même ordre que le premier
terme, donc
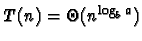 .
Ainsi, si
.
Ainsi, si
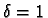 et
a>b (cas de la multiplication matricielle de Strassen, où
a=7 et b=2), on a
et
a>b (cas de la multiplication matricielle de Strassen, où
a=7 et b=2), on a
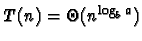 ;
;
-
Si
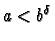 ,
le terme dominant est
,
le terme dominant est
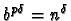 ,
donc
,
donc
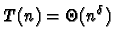 .
La décomposition du problème ne conduit
dans ce dernier cas à aucune accélération, les opérations de
décomposition et recomposition étant dominantes. C'est le cas de
l'équation
T(n) = 2T(n/2) + n2.
.
La décomposition du problème ne conduit
dans ce dernier cas à aucune accélération, les opérations de
décomposition et recomposition étant dominantes. C'est le cas de
l'équation
T(n) = 2T(n/2) + n2.





Next: La transformée de Fourier
Up: Algorithmes
Previous: L'algorithme
R. Lalement
2000-10-23
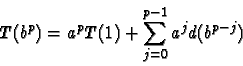
![]() .
On a
.
On a