La transformée de Fourier rapide

   

La FFT, ou transformée de Fourier rapide, est l'un des quelques algorithmes dont la publication a provoqué une véritable révolution dans le champ technique. Généralement associé aux noms de J.W. Cooley et J.W. Tuckey qui l'ont publié en 1965, cet algorithme de calcul de la transformée de Fourier discrète avait été maintes fois << redécouvert >> depuis Gauss, notamment par Danielson et Lanczos en 1942. La FFT permet de ramener le calcul de la transformée de Fourier discrète de N² à $N\log N$ opérations ; cette réduction de complexité suffit à faire passer d'impossibles à facilement résolubles nombre de problèmes.

La transformée de Fourier discrète d'un n-uplet de nombres complexes $a = (a_0, \ldots, a_{n-1})$ est le n-uplet $\hat{a} = (\hat{a}_0, \ldots, \hat{a}_{n-1})$ défini par

$$\hat{a}_q = \sum_{p=0}^{n-1} a_p \omega_n^{pq}$$

où $\omega_n = e^{2\pi i/n}$. Notons que $\hat{a}_{q+n} = \hat{a}_q$ et que pour n=1, ceci se réduit en $\hat{a} = a$. La transformée inverse se calcule ainsi :

$$a_p = \frac{1}{n} \sum_{q=0}^{n-1} \hat{a}_q \omega_n^{-pq}$$

Supposons que n=2m et séparons les éléments de a d'indices pairs de ceux d'indices impairs :

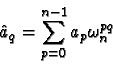
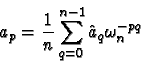
$$\begin{eqnarray*}a^{[0]} &= &(a_0, a_2, \ldots, a_{n-2}) \\ a^{[1]} &= &(a_1, a_3, \ldots, a_{n-1}) \end{eqnarray*}$$

Alors, en séparant la somme en deux termes regroupant d'une part les p=2j et d'autre part les p=2j+1, et en utilisant l'égalité $\omega_{2m}^{2jq} = \omega_{m}^{jq}$ :

$$\begin{eqnarray*}\hat{a}_q &= &\sum_{p=0}^{n-1} a_p \omega_n^{pq} \qquad (0\le q... ... \omega_n^q \hat{a}^{[1]}_{q-m} \quad\mbox{, si } m\le q\le n-1 \end{eqnarray*}$$

Cette dernière expression utilise la propriété de périodicité :

$$\begin{eqnarray*}\hat{a}^{[0]}_{q+m} &= &\hat{a}^{[0]}_q \\ \hat{a}^{[1]}_{q+m} &= &\hat{a}^{[1]}_q \end{eqnarray*}$$

Ainsi, pour calculer la transformée de Fourier sur n points, il suffit de calculer deux transformées de Fourier sur n/2 points, de faire nmultiplications et n additions. Si n est une puissance de 2, cette décomposition peut s'appliquer récursivement, ce qui donne pour équation de complexité : $T(n) = 2T(n/2) + \Theta(n)$. Il en résulte une complexité en $\Theta(n\log n)$ opérations.

Il existe aussi une FFT sur l'anneau Z/NZ des entiers modulo N, quand N = 2^tn/2 +1, t est un entier quelconque ; on pose $\omega = 2^t$, qui est une racine n-ème principale de l'unité dans Z/NZ ; on a toujours n=2^h. Par exemple, quand t=2 et n=2³=8, on a N=257, et $\omega=2^2=4$ ; un n-uplet et sa transformée sont :

$$\begin{eqnarray*}a &= &(255, 8, 0, 226, 37, 240, 3, 0) \\ \hat{a} &= &(255, 85, 127, 200, 78, 255, 194, 75) \end{eqnarray*}$$

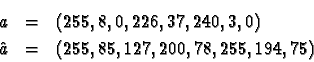
Pour traiter de façon identique le cas complexe et le cas modulo N, on utilise l'interface suivante, la première méthode servant à injecter un entier dans l'anneau (entier(0) est le zéro et entier(1) est l'unité de l'anneau) :

interface Nombre {
    Nombre entier(int i);
    Nombre add(Nombre y);
    Nombre sub(Nombre y);
    Nombre mult(Nombre y);
}

On supposera que l'on dispose d'implémentations Complexe et EntierModulo de cette interface.

La définition récursive de la FFT résulte directement de cette décomposition. La figure 2.29 représente l'arbre des invocations de ce calcul récursif
 
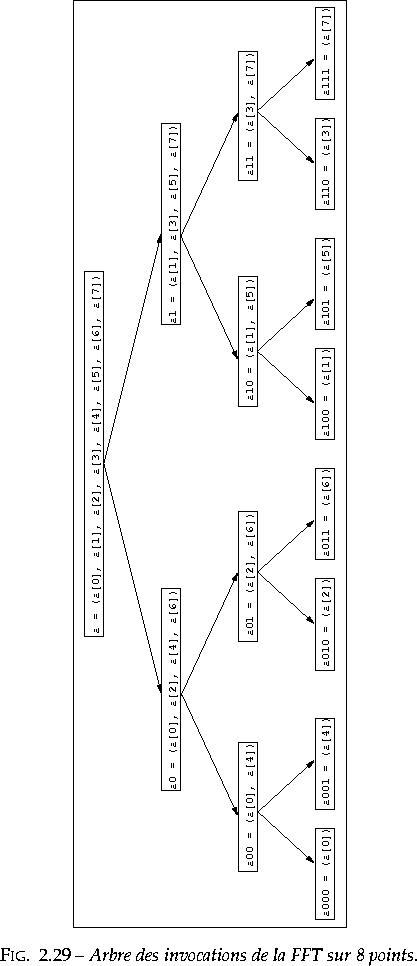
pour n=8 points : aux feuilles, la FFT sur 1 point, qui est l'identité. L'ordre dans lequel les a_p sont rangés dans les feuilles, de gauche à droite, est l'inverse de la représentation binaire de p. La fonction miroir(h,p) calcule cet inverse binaire de p, pour $0\le p\le 2^h-1$ ; par exemple, miroir(3,3) =miroir(3, 011₂) = 110₂ = 6 ; on utilise les opérateurs binaires <<, >>, &, | et ^, plus efficaces pour opérer au niveau des bits d'un entier ; pour h fixé, cette fonction est une involution : miroir(h, miroir(h, n)) = n.

  static int miroir(int h, int n) {
    int r;                      // Résultat
    for (r = 0; h > 0; h--) {
      // A chaque itération le bit de droite de n est
      // est tranféré dans r comme bit de droite
      r <<= 1;          // Un nouveau bit à droite
      r |= (n & 1);     // Positionnement de ce bit 
      n >>= 1;          // Effacement du bit de droite de n
    }
    return r;
  }

On va donc commencer par permuter le n-uplet a pour ranger ses éléments dans cet ordre, ce qui va permettra de construire un algorithme itératif, qui parcourt l'arbre des feuilles vers la racine :

  static void permuteTableau(Object[] a) {
    int h = log2(a.length);     // On suppose a.length = 2^h
    int i,j;                   
    
    for (i = 0; i < a.length; i++) {
      if ((j = miroir(h, i)) < i) {
        Object tmp = a[i];
        a[i] = a[j];
        a[j] = tmp;
      }
    }
  }

En utilisant la périodicité de la transformée de Fourier, et l'égalité $\omega_n^m = -1$, on peut réécrire la dernière expression de $\hat{a}$:

$$\begin{array}{rcl} \hat{a}_q &= &\hat{a}^{[0]}_q + \omega_n^... ...- \omega_n^q \hat{a}^{[1]}_q \end{array}\qquad (0\le q\le m-1)$$

Cette transformation, de la forme $(x,y) \mapsto (x+\alpha y, x-\alpha y)$, est appelée un papillon (en anglais, butterfly) ; on l'appliquera successivement avec $\alpha = 1$, $\omega$, $\omega^2$, ..., $\omega^{m-1}$. La fonction butterfly() s'écrit :

  static void butterfly(Nombre[] a, int i, int j, Nombre alpha) {
    Nombre u = a[i];
    Nombre v = alpha.mult(a[j]);
    a[i] = u.add(v);
    a[j] = u.sub(v);
  }

Voici enfin la fonction de calcul de la FFT ; le paramètre a est un tableau dont la longueur n doit être une puissance de 2, et racine est une racine n-ième de l'unité :

  public static Nombre[] fft(Nombre[] a, Nombre racine) {
    int h = log2(a.length);
    int i, j, l;
    int pas = 1;
    
    // Calcul des racine^{2^l} pour 0 <= l < h
    Nombre[] puissancesRacine = new Nombre[h];
    puissancesRacine[0] = racine;
    for(l = 1; l< h; l++)
      puissancesRacine[l] = 
        puissancesRacine[l-1].mult(puissancesRacine[l-1]);
    
    // Permutation du tableau
    permuteTableau(a);
    
    // Itération 
    for(l = h-1, pas = 1; l >=0; l--, pas *= 2) {
      Nombre alpha = racine.Entier(1); // Unité
      for (i = 0; i < pas; i++) {
        for (j = i; j < a.length; j += 2*pas) {
          butterfly(a, j, j+pas, alpha);
        }
        alpha = alpha.mult(puissancesRacine[l]);
      }
    }
    return a;
  }