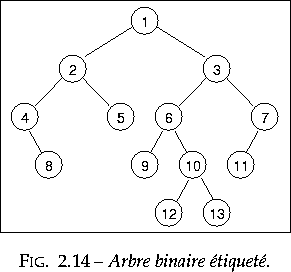
Un arbre binaire est soit l'arbre vide, soit formé de deux arbres binaires, appelés fils gauche et fils droit. On considère souvent des arbres étiquetés (dans les exemples qui suivent, ces étiquettes seront des entiers, mais elles peuvent être de n'importe quel type) : un arbre binaire étiqueté (en anglais labelled binary tree), ce qu'on abrégera ici en << arbre >>, est soit l'arbre vide, soit formé d'une étiquette et de deux arbres, appelés fils gauche et fils droit. Un sous-arbre d'un arbre est soit un fils, soit un sous-arbre d'un fils. Un arbre vide n'a pas de sous-arbre. Les feuilles d'un arbre sont des sous-arbres dont les deux fils sont des arbres vides. La figure 2.14 représente un arbre binaire étiqueté par des entiers.
Comme le suggère cette représentation, un arbre binaire a une
structure de graphe non orienté : l'ensemble de ses sommets, ou
n
uds, est formé de l'arbre et de tous ses sous-arbres non
vides, et il y a une arête entre u et v si v est un fils de
u. Ce graphe est connexe et sans circuit, autrement dit c'est un
arbre, au sens de la théorie des graphes (§ 2.12). Un arbre
binaire a en fait une structure plus riche : il est aussi
enraciné et ordonné. Sa racine est le sommet associé à
l'arbre lui-même, et chaque nud est la racine du sous-arbre
correspondant ; les nuds qui ne sont pas des feuilles sont dits
internes. Par exemple, l'arbre de la figure 2.14 est non
vide ; il a donc une racine, étiquetée par 1, et deux fils ; ses
nuds internes sont étiquetés par 1, 2, 3, 4, 6, 7, 10 ; ses
feuilles sont étiquetées par 8, 5, 9, 12, 13, 11 ; il a en tout 13
nuds. De plus, un arbre binaire est ordonné au sens où l'on peut
distinguer le sous-arbre gauche et le sous-arbre droit.
