Contents
Please launch software Scilab on your computer. To install Scilab, please consult
http://www.scilab.org.
On this Internet page, you will find Scilab instructions lines starting with -->. You
will copy them (or paste them by copy-paste) in the Scilab window to see how they
are executed. Beware not to copy the prompt -->.
Every line starting with // is a line of comments and is not executed by
Scilab.
1 Scalars, vectors, matrices
- scalars
To begin, just type “x=8” in the Scilab window.
-->x=8
// Scilab affects the value 8 to the variable x
-->5
// Scilab affects the value 5 to the variable ans
// (for answer)
-->ans^2
// ans to the power 2 gives 25
-->abs(-5)
// absolute value
-->m=10^6
-->sqrt(m)
// square root
-->y=%e
-->log(y)
// %e is the constant e
-->sin(%pi)
// %pi is the constant pi
-->1+%eps
// %eps is the precision
- complex numbers
-->%i
-->%i^2
-->x=3-4*%i
-->abs(x)
// modulus
- vectors
-->v=[3.8,-4,%pi/6]
-->size(v)
// dimensions of v : 1 row and 3 columns
-->w=v'
// transposition
-->x=[1,2]; y=[3,4,5]
-->z=[x,y];
// construction of a vector by assembling blocks
-->t=[4:9]
// vector made of reals ranging from 4 to 9 by step 1
// (implicit set: 1 by defect)
-->t=[4:1:9]
// the same but with explicit step
-->t=[0:0.1:1]
// vector made of reals ranging from 0 to 1 by step 0.1
-->t=[0:0.1:%pi]
-->u=%e*[1:2:8]'
-->size(u)
-->s=ones(u)
// s is a vector with the same dimension as u
// all the elements of s are equal to 1
-->zeros(u)
// vector with the same dimension as u
// all the elements are equal to 0
-->t=rand(1,5)
// t is a vector with 1 row and 5 columns
// whose elements are randomly chosen in the interval [0,1]
-->v=rand(s)
// v is a vector with the same dimension as s
// whose elements are randomly chosen in the interval [0,1]
- matrices
-->[1,2;3,4]
-->[11,12,13,14,15,16,17,18,19;21,22,23,24,25,...
-->26,27,28,29;31,32,33,34,35,36,37,38,39]
// when an instruction is too long to hold in a single line
// interrupt it by ... before changing line
-->diag([5 4 3])
// diagonal matrix
-->eye(6,6)
// matrix full of 0 except for the diagonal filled with 1
-->B=eye(6,7)
-->A=ones(3,7)
-->C=[A;(-6)*B]
-->D=zeros(2,5)
-->E=rand(D)
-->rand(2,5)
Question 1
- Build a matrix with 4 rows and 9 columns with 1 on the first row and 0 everywhere
else. Use the above examples to build it by blocks.
- Build a matrix with 3 rows and 5 columns: the first column is made of 2, the second of
integers ranging from 1 to 3, and the rest is made of -1.
2 Usual vectorial operations
- functions (with vector arguments)
-->u=2*%pi*rand()
// u is randomly chosen in [0,2*pi]
-->w=[cos(u) sin(u)]
-->norm(w)
// the euclidian norm of w is 1 since cos^2(u)+sin^2(u) = 1
-->norm(w,1)
// the 1-norm of w is |cos(u)|+|sin(u)|
-->t=2*%pi*rand(1,6)
-->v=sin(t)
-->maxi(v)
// the maximum value of the elements of v
-->[m,k]=maxi(v)
// the maximum value of the elements of v is m
// this maximum value m is reached at elements with index k : m=v(k)
-->[m,k]=mini(v)
-->sign(v)
// signe 1 (+) ou -1 (-) and sign(0)=0
- logical operations
-->1==0
// is 1 equal to 0? the answer is F (false)
-->1~=0
// is 1 different from 0? the answer is T (true)
-->1==0 & 1~=0
// and: the answer is F (false)
-->1==0 | 1~=0
// or: the answer is T (true)
-->t=[0:%pi/2:2*%pi]
-->v=sin(t)
-->v>0
// returns a vector whose elements are T (true) or F (false)
// T if the correspond element is >0, F if not
-->v>=0
-->v(v>=0)
// extracts the nonnegative elements of v
// this vector may have less elements than v
-->bool2s(v>=0)
// converts the T and F in 1 and 0
- addition
-->w=1:9
-->sum(w)
// gives the sum of all elements de w
-->cumsum(w)
// this is a vector consisting of the sequence of cumulated sums
-->A=rand(2,3)
-->B=sin(A)
-->A+B
-->G=[ones(1,4); 2*ones(1,4)]
-->sum(G,'c')
// sums the rows of the matrix G:
// the resulting object is a column vector ('c' for column)
-->sum(G,'r')
// sums the columns of the matrix G:
// the resulting object is a row vector ('r' for row)
- transposition
-->A'
- rank
-->rank(A)
- multiplication
-->A'*A
-->A*A'
-->C=eye(A)
-->A'*C
- determinant
-->A=[1,2;3,4]
-->det(A)
-->u=%pi/4 -100*%eps
-->det([cos(u) sin(u); sin(u) cos(u)])
- exponentiation
-->D=rand(3,3)
-->expm(D)
// matrix exponential: EXPM(d)=I +D + D^2/2! + D^3/3! + ...
-->exp(D)
// beware: exp(D) is a matrix in which each element is the
// exponential of the corresponding element of D
- extracting elements from a vector
-->w=1:2:9
-->w(2)
-->w($) // last element
-->w($-1) // before-last element
- extracting submatrices
-->E=[11:19;21:29;31:39;41:49;51:59;61:69]
-->E(1,1) // the element of row 1 column 1
-->E(3,4) // the element of row 3 column 4
-->E(1,:) // the whole row 1
-->E(:,5) // the whole column 5
-->E(2:4,:)
// the submatrix made of rows ranging from 2 to 4
-->E(2:3,7:9)
// the submatrix made of elements belonging both to
// rows ranging from 2 to 3 and to columns ranging from 7 to 9
-->E([1,3,5],[2,4,6,8])
// the submatrix made of elements belonging both to
// rows ranging 1 3 5 and to columns 2 4 6 8
-->E(:,$) // last column
-->E(:,$-1) // before-last column
-->E(2:$,:)
// the submatrix made of rows ranging from 2 to the last row
-->E(2:($-1),:)
// the submatrix made of rows ranging from 2 to the before-last row
- other functions
-->a=int(20*rand(1,10))
// integer part
-->[sa,ia]=sort(a)
// sorting: sa is the sorted vector, ia the corresponding indexes
3 Term by term vectorial operations
- term by term multiplication
-->x=[1 2 3]
-->x.*x
-->y=[-6 12 8]
-->x.*y
-->A=rand(2,3);
-->B=ones(A);
-->A.*B
- term by term division
-->x=[1 2 3]
-->y=1 ./x
// a space follows the 1, for if not 1. would be interpreted as 1.0 and
// the operation would be / (linear system resolution)
-->x.*y
-->A=rand(2,3);
-->B=rand(A);
-->A./B
- term by term power
-->x=[1 2 3]
-->y=x.^2
-->z=x.^[5 10 -2]
-->A=rand(2,3);
-->A.^3
-->B=rand(A);
-->A.^B
Question 2
- Build a matrix A=rand(5,3). This matrix has three columns: multiply the first column
by 5, the second by 2 and the last by 7; use only the following Scilab operations *, .*
and ones.
4 2D graphics
For planar graphs, you have Scilab macros plot (elementary) and plot2d (with many
options).
-->x=0.1:0.1:10;
-->y=sin(x)./x;
-->plot(x,y)
Execute the instruction help plot2d to have information about the many options of
plot2d.
-->x=0.1:0.1:10;
-->y=sin(x)./x;
-->z=cos(x)./x;
-->xbasc();
// erase the graphic content of the window
-->plot2d(x,y);plot2d(x,z)
// both graphics are superposed
-->xbasc();plot2d([x ; x]',[y ; z]')
// the same, but both graphics are drawn each with its own color
// [x ; x]' is a matrix with 2 colonnes, as is [y ; z]'
// so that two curves are drawn
-->xbasc();plot2d([x' x'],[y' z'])
// gives the same result since [x ; x]' coincides with [x' x']
// and [y' z'] avec [y ; z]'
--> xset("window",2)
// window 2 is now active and future graphic instructions will
// appear in this window
--> plot2d(x,y)
--> xset("window",3) ; plot2d(x,z)
--> xdel(0)
// deletes the window 0
--> xdel(2:3);
// deletes the windows from 2 to 3
-->r=rand(100,1)
-->xbasc();plot2d(r)
-->x=(1:100)';
-->xbasc();plot2d(x,r,style=-5)
-->s=rand(100,1);
-->xbasc()
-->plot2d(r,s,-2)
-->y=[6:-1:0,1:5] ; x =[y,y,y,y,y];
-->xbasc();plot2d(0:60,[x,6]);
// a simple graphic
-->xbasc();plot2d(0:60,[x,6],strf="011",rect=[0,0,60,6])
// the frame is fixed by rect =[xmin,ymin,xmax,ymax]
-->xbasc();plot2d(0:60,[x,6],strf="011",rect=[0,0,60,6],...
nax=[0,5,0,6])
// when an instruction is too long to hold in a single line
// interrupt it by ... before changing line
// nax=[0,5,0,6] fixes divisions and subdivisions on the axes
// execute instruction help plot2d to see all the options
-->x=1:10;
-->xbasc();plot2d2(x,x);
-->histplot(10,r)
// draws the histogram of 100 reals randomly chosen in [0,1]
-->xbasc()
-->histplot(0:0.2:1,r)
// the same but in choosing the sizes of the classes
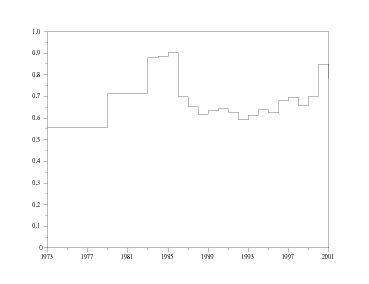
Question 3 Plot the years in abcissa and the price of gasoline (euros of 2001) in ordinates. Take
care that the ordinates graph ranges from 0 to 1 euro.
annees=[1973 1979 1983:2001]
// only some years are available
prix_gazole_EC2001=[0.557 0.715 0.879 0.885 0.902 0.699 0.652 0.618 ...
0.633 0.643 0.627 0.592 0.614 0.638 0.624 0.681 0.697 0.658 0.702 0.848 0.783]
// price of gasoline (euros of 2001)
5 Programming
Scilab is an interpreted language, where the transmission of the arguments is made by value, even
for the objects of matrix type. It is thus recommended to avoid the loops, as they can prove
ineffective in term of computation time. For that purpose, it is better, if possible, to make use of
the vectorial operators who perform the same operations.
We recommend to use a text editor (Emacs), to open a file (for instance
file_name.sce), to write the code lines and to execute them inside Scilab with the
instruction exec("file_name.sce").
- condition if
p=0.4
y=rand(1)
if y< p then x=1;
elseif y>= p then x=0;
end
x
- boucles while
p=0.2
y=rand(1);
compteur=1;
while y >=p do compteur=compteur+1; y=rand(1); end
compteur
- boucles for
N=500;
y=rand(1,N)-0.5*ones(1,N);
x=sign(y);
for i=2:N,x(i)=x(i-1)+x(i);end;
xbasc();plot2d(1:N,x)
x1=cumsum(sign(y));
norm(x1-x)
6 Scilab functions
One may define a Scilab function interactively. However, it is more practical and
flexible to write the Scilab code in a file with a text editor. One can mix
Scilabinstructions Scilab and functions definitions in a same file, named with the
extension .sce.
The beginning of a Scilab function is
function [<arguments de retour>]=<nom>(<arguments d'entrée>)
and the code ends with the keyword endfunction.
function [y]=densite(x), y=1 ./(%pi*sqrt(x.*(1-x))), endfunction;
x=0.01:0.01:0.99;y=densite(x);
xbasc(); plot(x,y);
function [H] = Heavyside(x)
// Heavyside function
H = bool2s(x>=0)
// Heavyside(0)=1
endfunction
x=-1:0.2:1; xbasc(); plot2d2(x,Heavyside(x),rect=[-1,-0.1,1,1.2]);
Question 4 Write the function sinus cardinal (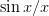 ).
).
A Scilab function in Scilab may have several arguments, scalars or vectors.
function [y]=Gauss(x,mu,sigma)
// mu and sigma are scalars
// x may be a vector of any dimensions
y=1 ./(sigma*sqrt(2*%pi))*exp(-((x-mu)/sigma).^2/2)
endfunction;
function [Y]=Normal(X,Mu,Sigma)
// Mu is a row vector with dimensions [1,dim]
// Sigma is a positive symmetric matrix with dimensions [dim,dim]
// x may only be a vector with dimensions [1,dim]
[lhs,dim]=size(Mu)
Y=1/ sqrt( (2*%pi)^dim * det(Sigma) ) * ...
exp(- (X-Mu)*inv(Sigma)*(X-Mu)' / 2 )
endfunction;
A Scilab function in Scilab may have several outputs.
function [H,plus] = Heavyside_plus(x)
// Heavyside function
H = maxi(sign(x),0);
// Heavyside(0)=1
plus=maxi(x,0)
// Function +
endfunction
[H,plus] = Heavyside_plus(-1:0.2:1)
function [x]=permutation_lent(n)
// permutation aléatoire de {1,...,n}
// version avec des boucles
x=ones(1,n);
for i=2:n,k=0;
for j=1:1+int(rand(1)*(n-i+2));k=k+1;
while x(k)>1 do
k=k+1;
end;
end;
x(k)=i;
end;
endfunction
function [x]=permutation_rapide(n)
// permutation aléatoire de {1,...,n}
x=grand(1,'prm',[1:n]')
endfunction
// loading of function permutation_lent :
-->exec("nom_du_fichier.sce")
// the function is now loaded
-->permutation_lent
// call of function permutation_lent
-->permutation_lent(100)
7 Simulation of dynamic systems in discrete time
We consider the discrete time dynamics system in 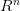 :
:
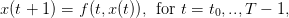 | (1) |
starting from initial state 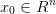 at time
at time 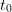
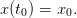 | (2) |
Knowing function 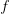 and
and 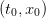 , we are able to compute the whole sequence
, we are able to compute the whole sequence
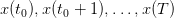 solution of the problem.
solution of the problem.
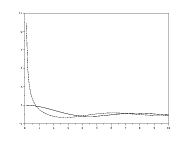
7.1 Population dynamics in ecology
Consider the population dynamics
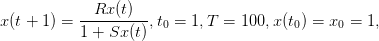
with parameters 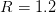 and
and 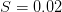 .
.
t0=1;x0=1;
x(t0)=x0; T=100; R=1.2; S=0.02;
function y=f(t,x)
y=R*x./(1+S*x)
endfunction
for (t=t0:1:T)
x(t+1)=f(t,x(t));
end;
plot2d(t0:T+1,x(t0:T+1))
7.2 Carbon cycle
Consider the carbon cycle
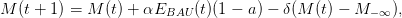
starting from initial conditions 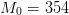 (ppm) at year
(ppm) at year 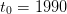 with time horizon
with time horizon
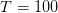 . The parameters are
. The parameters are 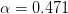 , preindustrial concentration
, preindustrial concentration 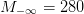 ,
removal rate
,
removal rate 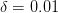 . It is assumed that the ”business as usual” CO
. It is assumed that the ”business as usual” CO emissions path
is
emissions path
is
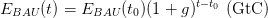 with the emissions growth set to
with the emissions growth set to 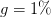 and initial emissions to
and initial emissions to 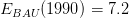 (GtC).
(GtC).
t0=1990; T=2100; M_0=354;
alpha=0.471; M_infty=280; delta=1/120; sigma=0.519;
E_BAU=7.2;g=0.01
a=0;
function y=EBAU(t)
y=E_BAU*(1+g)^(t-t0);
endfunction
function y=f(t,M)
y=M+alpha*EBAU(t)*(1-a)-delta*(M-M_infty);
endfunction
x(t0)=M_0;
for (t=t0:1:T)
x(t+1)=f(t,x(t));
end;
plot2d(t0:T+1,x(t0:T+1),rect=[t0,0,T+1,1000])
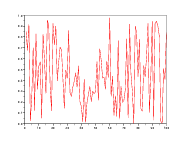
7.3 An ecosystem
We consider two populations 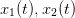 interacting within a trophic web. The dynamics based on
a Lotka-Volterra form is characterized by
interacting within a trophic web. The dynamics based on
a Lotka-Volterra form is characterized by
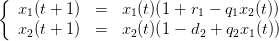 | (3) |
where 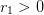 is the intrinsic growth of prey while
is the intrinsic growth of prey while 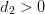 is the intrinsic decrease of
predator. Parameters
is the intrinsic decrease of
predator. Parameters 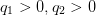 are related to the catchability and efficiency of trophic
relations.
are related to the catchability and efficiency of trophic
relations.
t0=1;x0=[1;1];
T=100;
r_1=0.1; d_2=0.1; q_1=0.1; q_2=0.2;
function y=f(t,x)
x_1=x(1);x_2=x(2);
y_1=x_1.*(1+r_1-q_1*x_2);
y_2=x_2.*(1-d_2+q_2*x_1);
y=[y_1;y_2];
endfunction
x=zeros(2,T+1);
x(:,t0)=x0;
for (t=t0:1:T)
x(:,t+1)=f(t,x(:,t));
end;
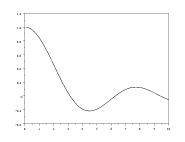
plot2d(t0:T+1,x(:,t0:T+1)')

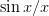 ).
).
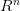 :
:
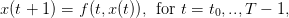
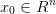 at time
at time 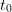
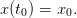
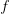 and
and 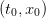 , we are able to compute the whole sequence
, we are able to compute the whole sequence
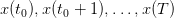 solution of the problem.
solution of the problem.
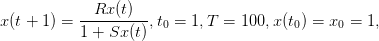
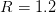 and
and 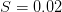 .
.
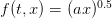 where
where 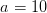 .
Compare the behavior of the solutions
.
Compare the behavior of the solutions 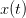 .
.
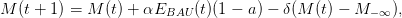
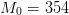 (ppm) at year
(ppm) at year 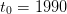 with time horizon
with time horizon
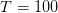 . The parameters are
. The parameters are 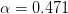 , preindustrial concentration
, preindustrial concentration 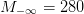 ,
removal rate
,
removal rate 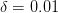 . It is assumed that the ”business as usual” CO
. It is assumed that the ”business as usual” CO emissions path
is
emissions path
is
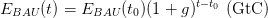
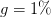 and initial emissions to
and initial emissions to 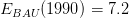 (GtC).
(GtC).
 (
(![a ∈ [0, 1]](english_intro_scilab34x.png) ) to compare the behavior of the
concentrations profile
) to compare the behavior of the
concentrations profile 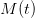 .
.
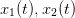 interacting within a trophic web. The dynamics based on
a Lotka-Volterra form is characterized by
interacting within a trophic web. The dynamics based on
a Lotka-Volterra form is characterized by
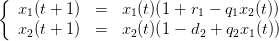
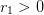 is the intrinsic growth of prey while
is the intrinsic growth of prey while 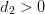 is the intrinsic decrease of
predator. Parameters
is the intrinsic decrease of
predator. Parameters 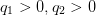 are related to the catchability and efficiency of trophic
relations.
are related to the catchability and efficiency of trophic
relations.
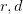 or
or 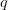 to compare the behavior of the populations
to compare the behavior of the populations
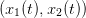 .
.