Contents
1 Zéros avec fsolve
-->help fsolve
1.1 Zéros de fonction scalaire
- zéro de polynôme
-->function [y]=fct(x) , y=2*x^3-30*x^2-3*x+200, endfunction
-->x=[-3:0.1:15];xbasc();plot2d(x,fct(x));
--> x1=fsolve(-1,fct)
-->fct(x1)
--> x2=fsolve(1,fct)
-->fct(x2)
--> x3=fsolve(11,fct)
-->fct(x3)
- zéro de polynôme, avec gradient
-->function [y]=fct(x) , y=2*x^3-30*x^2-3*x+200, endfunction
-->function [y]=grad_fct(x) , y=6*x^2-60*x-3, endfunction
-->x=[-3:0.1:15];xbasc();plot2d(x,fct(x));
--> x1=fsolve(-1,fct,grad_fct)
-->fct(x1)
--> x2=fsolve(1,fct,grad_fct)
-->fct(x2)
--> x3=fsolve(11,fct,grad_fct)
-->fct(x3)
1.2 Intersection de coniques
- Fonctions de définition des coniques
-->function [z]=conique1(x,y) , z=2*x^2+ 5*y^2-30*x+20, endfunction
-->function [z]=conique2(x,y) , z=2*x^2 -y^2-3*y-20, endfunction
- On trace les coniques en dessinant les deux contours de niveau 0 de conique1 et
conique2
-->help fcontour2d
-->x=-2:10;
-->y=-10:10;
-->xbasc();
-->fcontour2d(x,y,conique1,[0,0],style=[9,9])
// on trace conique1(x,y)=0
// on est obligé de poser [0,0], et non pas 0 qui pourrait être confondu
// avec l'entier désignant le nombre de courbes de niveau à tracer
-->fcontour2d(x,y,conique2,[0,0],style=[12,12],strf="000")
// on superpose le deuxième contour
- Recherche d'un point d'intersection
-->function [Y]=coniques(X) , Y=[conique1(X(1),X(2)),...
conique2(X(1),X(2))], endfunction
-->rep=fsolve([-1,1],coniques)
-->coniques(rep) // on vérifie le calcul
- On rajoute le point sur le dessin
-->xpolys(rep(1),rep(2),-1)
Question 1 Choisir une fonction de 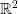 dans
dans 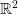 , la programmer, chercher un zéro,
puis représenter ses courbes de niveau.
, la programmer, chercher un zéro,
puis représenter ses courbes de niveau.
2 Intégration d'équations différentielles avec ode
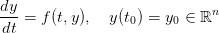
-->help ode
2.1 Équations différentielles scalaires autonomes
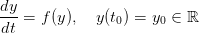
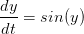
-->function [ydot]=f(t,y) , ydot=sin(y), endfunction
//attention ! on écrit f(t,y) même si f ne dépend pas de t
-->y0=0.2;t0=0;t=0:0.1:15;
-->y=ode(y0,t0,t,f);
-->xbasc(); plot2d(t,y)
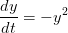
-->function [ydot]=f(t,y) , ydot=-y^2, endfunction
-->y0=0.2;t0=0;t=0:0.1:30;
-->y=ode(y0,t0,t,f);
-->xbasc(); plot2d(t,y)
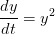
-->function [ydot]=f(t,y) , ydot=y^2, endfunction
-->y0=0.2;t0=0;t=0:0.1:30;
-->y=ode(y0,t0,t,f);
-->xbasc(); plot2d(t,y)
Question 2 Que se passe-t-il dans ce dernier cas ? Quel est le rapport avec la solution de
l'équation différentielle 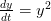 ?
?
2.2 Équation différentielle scalaire non autonome
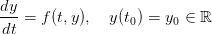
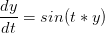
-->function [ydot]=f(t,y) , ydot=sin(t*y), endfunction
-->y0=0.2;t0=0;t=0:0.1:15;
-->y=ode(y0,t0,t,f);
-->xbasc(); plot2d(t,y)
2.3 Système différentiel
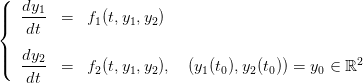
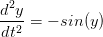
-->function [z]=fct1(y1,y2) , z=y2, endfunction
-->function [z]=fct2(y1,y2) , z=-sin(y1), endfunction
-->function [Z]=fct(t,Y) , Z=[fct1(Y(1),Y(2)),fct2(Y(1),Y(2))], endfunction
-->y0=[0.3,0.2]';t0=0;t=0:0.1:30;
-->y=ode(y0,t0,t,fct);
-->xbasc(); plot2d(t,y(1,:))
Question 3 Programmer le système différentiel
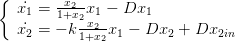 | (1) |
Choisir des valeurs positives pour 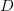 et
et 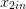 . Résoudre numériquement et tracer des
trajectoires.
. Résoudre numériquement et tracer des
trajectoires.
3 Optimisation avec optim
-->help optim
3.1 Minimum d'une fonction de deux variables, sans contraintes
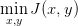
Un exemple simple : optimiser 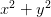 sur
sur 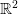 .
.
-->function [f,g,ind]=cost(x,ind)
f=x(1)^2+x(2)^2, g=[2*x(1);2*x(2)]
endfunction
// g est le gradient de f
// ici, ind est un paramètre non utilisé mais qui doit être présent
-->[f,xopt]=optim(cost,[1;2])
// le coût est quasi nul
3.2 Minimum d'une fonction de deux variables, avec contraintes
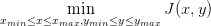
Le même problème que dans la section précédente mais sous contraintes : ![x ∈ [2,10]](intro_scilab_319x.png) et
et
![y ∈ [− 10,10]](intro_scilab_320x.png) . Noter que le minimum est atteint sur un bord.
. Noter que le minimum est atteint sur un bord.
-->function [z]=C(x,y) , z=x^2+y^2, endfunction
-->x=2:10;y=-10:10;
-->z=feval(x,y,C);
-->xbasc();
-->plot3d(x,y,z);
-->[f,xopt,gopt]=optim(cost,'b',[2;-10],[10;10],[5;5]);
// f n'est pas nul
// le gradient en xopt est perpendiculaire au bord
Question 4 Choisir une fonction de 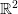 dans
dans 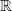 qui soit bornée supérieurement, la
programmer, chercher un maximum.
qui soit bornée supérieurement, la
programmer, chercher un maximum.
4 Hypermatrices
-->A= hypermat([2,2,2,2],rand(16,1));
-->B = A(1,:,2,:)
B =
(:,:,1,1)
! 0.3076091 0.2146008 !
(:,:,1,2)
! 0.3321719 0.5015342 !
-->B.entries
ans =
! 0.3076091 !
! 0.2146008 !
! 0.3321719 !
! 0.5015342 !
-->matrix(B.entries,2,2)
ans =
! 0.3076091 0.3321719 !
! 0.2146008 0.5015342 !
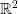 dans
dans 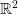 , la programmer, chercher un zéro,
puis représenter ses courbes de niveau.
, la programmer, chercher un zéro,
puis représenter ses courbes de niveau.
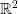 dans
dans 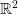 , la programmer, chercher un zéro,
puis représenter ses courbes de niveau.
, la programmer, chercher un zéro,
puis représenter ses courbes de niveau.
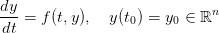
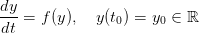
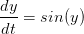
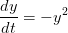
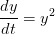
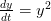 ?
?
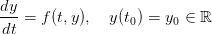
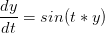
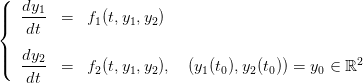
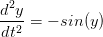
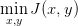
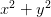 sur
sur 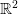 .
.
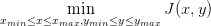
![x ∈ [2,10]](intro_scilab_319x.png) et
et
![y ∈ [− 10,10]](intro_scilab_320x.png) . Noter que le minimum est atteint sur un bord.
. Noter que le minimum est atteint sur un bord.
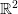 dans
dans 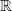 qui soit bornée supérieurement, la
programmer, chercher un maximum.
qui soit bornée supérieurement, la
programmer, chercher un maximum.