On considère le problème modèle
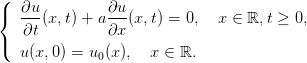 | (1) |
L’inconnue est la fonction u qui dépend de la coordonnée spatiale x et du temps t. Les données du problème sont la fonction u0 appelée condition initiale et le paramètre réel a appelé vitesse d’advection. On vérifie aisément que la solution de (1) est
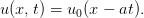 | (2) |
Une interprétation physique de l’équation (1) est la suivante : on considère un fleuve rectiligne
représenté par la droite réelle et qui s’écoule à la vitesse a. La quantité u(x,t) représente la
concentration au point x et à l’instant t d’un produit polluant qui a été déversé accidentellement
dans la fleuve à t = 0 selon le profil u0. Le polluant est transporté par l’écoulement et à
un temps t fixé, la fonction x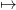 u(x,t) modélise la répartition de polluant le long du
fleuve.
u(x,t) modélise la répartition de polluant le long du
fleuve.
Pour simplifier, nous allons supposer que la donnée initiale u0 est périodique (en espace) de période L si bien que nous pouvons nous restreindre à l’intervalle x ∈ [0,L] et chercher la solution u satisfaisant
![(
|{ ∂∂ut(x,t) + a∂∂ux(x,t) = 0, x ∈ [0,L ],t ≥ 0,
u(x,0) = u (x), x ∈ [0,L ],
|( 0
u(L,t) = u(0,t), t ≥ 0.](advection3x.png) | (3) |
La dernière équation est une condition limite de périodicité.
Afin d’approcher numériquement la solution u, on se donne
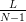 et un maillage uniforme
de l’intervalle [0,L] constitué des N points xi = (i − 1)δx, 1 ≤ i ≤ N;
et un maillage uniforme
de l’intervalle [0,L] constitué des N points xi = (i − 1)δx, 1 ≤ i ≤ N;
Notre objectif est d’évaluer des quantités Uin, 1 ≤ i ≤ N et n ≥ 0, telles que
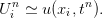
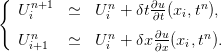
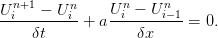 | (4) |
En réarrangeant (4), il vient
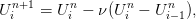 | (5) |
où nous avons posé
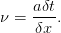 | (6) |
Ce paramètre, sans dimension physique et connu sous le nom de nombre de Courant, jouera un rôle déterminant par la suite.
L’équation (5) définit un schéma numérique qu’on appelera schéma upwind (la terminologie, inspirée de l’anglais, rappelle le fait que la dérivée en espace a été décalée dans la direction d’où provient le vent (ou le courant)). Notons que (5) est un schéma explicite : étant données les valeurs de Uin pour 0 ≤ i ≤ N, (5) permet de calculer explicitement les valeurs de U in+1 pour 0 ≤ i ≤ N. La simulation numérique s’arrête lorsque le temps courant tn dépasse un temps physique de simulation choisi à l’avance.
Il nous reste à approcher la condition initiale et la condition limite en écrivant
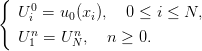
On écrira un script Scilab qu’on appelera script1.sce et qui comprendra 4 parties :
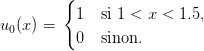 | (7) |
Pour la condition initiale, on utilisera la fonction bool2s dont on consultera l’aide en ligne (help → Scilab Programming → bool2s). La condition initiale sera programmée sous forme de fonction Scilab, ce qui devrait donner quelque chose comme
On notera que v est une variable locale à la fonction condinit.
(voir l’aide en ligne; la transposition permet de manipuler des vecteurs colonne ce qui est plus pratique pour la sortie graphique).
avant le démarrage de la boucle en temps et la commande
en dernière ligne du script Scilab. Le temps d’exécution écoulé entre les 2 appels de la fonction timer sera affiché dans la fenêtre Scilab.
Question 1 Augmenter progressivement le paramètre ν et observer les résultats. Quelle est la valeur critique?
Outre la condition initiale (7), on souhaite également pouvoir considérer la condition initiale
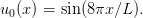 | (8) |
De plus, on souhaite avoir le choix entre 2 schémas numériques : le schéma upwind (5) et le schéma de Lax-Wendroff
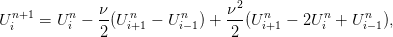 | (9) |
dont la justification sera étudiée en cours de Calcul Scientifique.
Ecrire un script Scilab qu’on appelera script2.sce et qui offre ces 2 options.
Question 2 Repartir de ν = 0.8 et essayer les 4 possibilités du couple condition initiale / schéma numérique. Quelles conclusions tirez-vous ? Augmenter progressivement ν pour le schéma de Lax-Wendroff et observer.
L’objectif de cette nouvelle étape est de pouvoir visualer la solution numérique au fil des itérations au lieu de visualiser uniquement sa valeur finale.
Partant du script script2.sce, on réalisera un nouveau script qu’on appelera script3.sce.
La commande driver("X11") permet d’accélérer l’affichage en ne stockant pas en mémoire toutes les données relatives au tracé de la courbe mais seulement les plus importantes (perte de la possibilité du zoom par exemple). La commande xset("pixmap",1) évitera le clignotement de la fenêtre lors de la boucle en temps.
La commande xset("wwpc") efface le contenu courant de la fenêtre graphique en mémoire. La commande xset("wshow") affiche dans la fenêtre graphique le contenu courant de la mémoire.
Question 3 Reprendre les essais précédents puis augmenter progressivement le paramètre ν et observer (pour le schéma de Lax-Wendroff, prendre ν = 1.2, ν = 1.5 et ν = 1.8). Quelles conclusions en tirer?
Nous allons modifier le schéma de Lax-Wendroff (9) en “implicitant le terme de diffusion” de la façon suivante
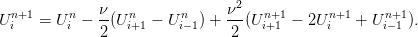 | (10) |
En introduisant les vecteurs Wn = (U
in −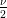 (Ui+1n − U
i−1n))
0≤i≤N−1 et Un+1 = (U
in+1)
0≤i≤N−1
ainsi que la matrice A d’ordre N − 1 donnée par
(Ui+1n − U
i−1n))
0≤i≤N−1 et Un+1 = (U
in+1)
0≤i≤N−1
ainsi que la matrice A d’ordre N − 1 donnée par
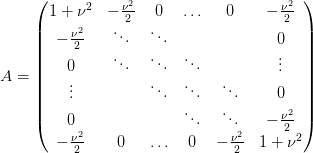
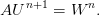
On constate que le schéma (10) n’est plus explicite mais implicite : si Un est connu, l’évaluation de Un+1 nécessite l’inversion d’un système linéaire. On s’attend donc à ce que le coût d’une itération dans (10) soit plus élevé que dans (9). Cependant, comme nous le verrons dans les expériences numériques, le schéma implicite (10) n’est pas limité par la valeur du nombre de Courant ν ce qui permet de considérer des pas de temps plus grands et donc de réaliser moins d’itérations en temps. Il n’est donc pas évident de déterminer a priori qui du schéma explicite ou implicite sera le plus performant.
Afin de réaliser les expériences numériques, on partira du script script3.sce dont on enlevera les parties relatives au schéma numérique. Le nouveau script sera appelé script4.sce.
soit inverser la matrice A avant les itérations en temps puis utiliser son inverse
Question 4 Comparer les 2 options pour l’inversion du système linéaire. Réaliser des expériences numériques en faisant varier le nombre de Courant. Discuter des performances relatives des schémas explicite et implicite.