Contents
1 Interpolation polynomiale: matrice de Vandermonde
On cherche à résoudre le problème d’interpolation polynomiale par résolution du système linéaire
obtenu en écrivant le système de n + 1 équations à n + 1 inconnues. On cherche donc l’unique
polynôme de degré n passant par les points (xi,fi)i=0,…,n. Les points (xi)i=0,…,n étant tous
distincts.
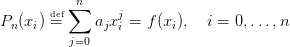 | (1) |
Soit en notation matricielle :
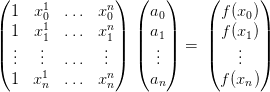 | (2) |
-->function y=f(x) ← La fonction que lflon cherche à interpoler
--> y=10./(1+x.*x)
-->endfunction
-->n=5 ;
-->x=linspace(-5,5,n)'; ← Les points dflinterpolation régulièrement espacés
-->V=(x*ones(1,n)).^( ones(n,1)*[0:n-1]);
← Construction de la matrice de Vandermonde
-->F=f(x); ← Les points dflinterpolation (x,F)
-->a = V F ← Résolution du système linéaire
a =
! 1. !
! 2.469D-17 !
! - 0.1710875 !
! - 9.876D-19 !
! 0.0053050 !
-->Pn=poly(a,"x","coeff") ← Construction du polynome dflinterpolation
Pn =
2 3 4
1 + 2.469D-17x - 0.1710875x - 9.876D-19x + 0.0053050x
-->nr=200;
-->xr=linspace(-5,5,nr)';
-->yr=f(xr);
-->yp=horner(Pn,xr); ← Évaluation du polynôme aux points xr avec horner
-->xbasc();
-->plot2d1("onn",xr,[yr,yp]) ← Voir figure 1
-->plot2d(x,F,-2);
Noter que le conditionnement du Vandermonde se dégrade très vite si l’on augmente le nombre
de points et que le système linéaire devient numériquement singulier pour n = 15 par
exemple :
-->vcond=[];
-->for n=[5,10,20]
--> x=linspace(-5,5,n)';
--> V=(x*ones(1,n)).^( ones(n,1)*[0:n-1]);
--> vcond=[vcond,cond(V)];
-->end
-->mprintf('n=5 %5.3e, n=10 %5.3e, n=20 %5.3e',vcond);
←Conditionnement pour 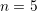 ,
, 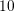 et
et 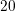 n=5 9.043e+02, n=10 5.083e+06, n=20 4.874e+14
n=5 9.043e+02, n=10 5.083e+06, n=20 4.874e+14
2 Polynôme d’interpolation de Lagrange
On utilise directement les polynômes de Lagrange pour réaliser l’interpolation polynomiale. Le
i-ème polynôme de Lagrange s’écrit :
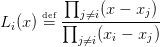 | (3) |
Et le polynôme d’interpolation s’écrit alors :
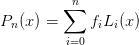 | (4) |
-->for n=5:20
--> x=linspace(-5,5,n)'; ← Les points dflinterpolation régulièrement espacés
--> F=f(x); ← Les points dflinterpolation (x,F),  --> clear P;
--> for i=1:n
--> y=x; y(i)=[]; ← Les
--> clear P;
--> for i=1:n
--> y=x; y(i)=[]; ← Les 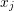 en retirant le
en retirant le  -ème
--> P(i)= poly(y,"x");
--> P(i)= P(i)/horner(P(i),x(i)); ← Le
-ème
--> P(i)= poly(y,"x");
--> P(i)= P(i)/horner(P(i),x(i)); ← Le  -ème polynôme de Lagrange
--> end
--> Pn= F'*P; ← Le polynôme dflinterpolation
--> nr=200;
--> xr=linspace(-5,5,nr)';
--> yr=f(xr);
--> yp=horner(Pn,xr);
--> xbasc();
--> plot2d1("onn",xr,[yr,yp])
--> plot2d(x,F,-2); ← Voir figure 2 pour n=13
--> Norme(n) =maxi(abs(yr-yp)); ← Un estimé de
-ème polynôme de Lagrange
--> end
--> Pn= F'*P; ← Le polynôme dflinterpolation
--> nr=200;
--> xr=linspace(-5,5,nr)';
--> yr=f(xr);
--> yp=horner(Pn,xr);
--> xbasc();
--> plot2d1("onn",xr,[yr,yp])
--> plot2d(x,F,-2); ← Voir figure 2 pour n=13
--> Norme(n) =maxi(abs(yr-yp)); ← Un estimé de 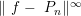 -->end
-->xbasc()
-->plot2d(Norme) ← Voir figure 3
-->end
-->xbasc()
-->plot2d(Norme) ← Voir figure 3
3 Évaluation du polynôme d’interpolation de Lagrange par l’algorithme de Neville
Pour évaluer le polynôme d’interpolation en un point on peut utiliser l’algorithme de Neville que
l’on rappelle ici. Cet algorithme permet en outre une estimation récursive quand on rajoute
progressivement des points d’interpolation. Soit Pi0…,ik le polynôme d’interpolation de
degré k passant par les points (xip,fip)p=0,…,k on établit facilement la formule récursive
suivante :
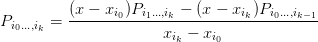 | (5) |
avec
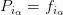 | (6) |
Cette formule nous permet de calculer Pn(x) = P0,…,n(x) pour une valeur de x fixée. Le
programme qui suit implémente l’algorithme de Neville, en travaillant de façon vectorielle sur un
ensemble de valeurs xnev pour lesquelles on souhaite obtenir la valeur de Pn(x) :
-->n=6;
-->x=linspace(-5,5,n)'; ← Les points dflinterpolation régulièrement espacés
-->F=f(x); ← Les points dflinterpolation (x,F),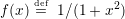 -->xnev= 1:3; ← Les points pour lesquels on veut la valeur de
-->xnev= 1:3; ← Les points pour lesquels on veut la valeur de 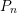 -->xc=ones(n,1)*xnev - x*ones(1,size(xnev,'*')); ← Matrice
-->xc=ones(n,1)*xnev - x*ones(1,size(xnev,'*')); ← Matrice 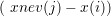 -->xd=x*ones(1,size(xnev,'*')) ;
--> Chaque colonne de la matrice col correspond aux
--> itérations de lflalgorithme de Neville pour une valeur fixée de x (xnev(j)).
--> A la fin des itérations col est un vecteur ligne
-->col=F*ones(1,size(xnev,'*')); ← Démarrage de la récursion
-->for k=1:n-1
--> col= xc(1:$-k,:).*col(2:$,:) - xc((1+k):$,:).*col(1:$-1,:);
--> col= col0./ (xd((1+k):$,:)-xd(1:$-k,:));
← Mise à jour (le nombre de lignes de col diminue de 1
-->end
-->clear P;
-->for i=1:n
--> y=x; y(i)=[]; P(i)= poly(y,"x"); P(i)= P(i)/horner(P(i),x(i));
-->end
-->Pn= F'*P;
-->y=horner(Pn,xnev); ← Comparons avec lflinterpolation de Lagrange
-->if norm(y-col) > 10*%eps then pause;end
-->xd=x*ones(1,size(xnev,'*')) ;
--> Chaque colonne de la matrice col correspond aux
--> itérations de lflalgorithme de Neville pour une valeur fixée de x (xnev(j)).
--> A la fin des itérations col est un vecteur ligne
-->col=F*ones(1,size(xnev,'*')); ← Démarrage de la récursion
-->for k=1:n-1
--> col= xc(1:$-k,:).*col(2:$,:) - xc((1+k):$,:).*col(1:$-1,:);
--> col= col0./ (xd((1+k):$,:)-xd(1:$-k,:));
← Mise à jour (le nombre de lignes de col diminue de 1
-->end
-->clear P;
-->for i=1:n
--> y=x; y(i)=[]; P(i)= poly(y,"x"); P(i)= P(i)/horner(P(i),x(i));
-->end
-->Pn= F'*P;
-->y=horner(Pn,xnev); ← Comparons avec lflinterpolation de Lagrange
-->if norm(y-col) > 10*%eps then pause;end
4 Différences divisées
L’algorithme de Neville est utilisé pour obtenir la valeur du polynôme d’interpolation en un point.
Quand on cherche l’expression du polynôme on peut utiliser les différences divisées et la
formule d’interpolation de Newton. On cherche le polynôme d’interpolation sous la
forme :
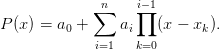 | (7) |
Les différences divisées se définissent alors par
 | (8) |
De la formule de récursion sur les polynômes Pi0…,ik on déduit, en identifiant les termes de plus
haut degrés, une formule de récursion sur les différences divisées :
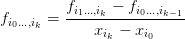 | (9) |
Le programme qui suit mets en œuvre cette récursion pour construire en Scilab le polynôme
d’interpolation. On notera aussi que cette formulation permet à nouveau une construction
récursive.
-->n=5;
-->x=linspace(-5,5,n)'; ← Les points dflinterpolation régulièrement espacés
-->F=f(x); ← Les points dflinterpolation (x,F),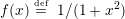 -->clear P;
-->for i=1:n-1
--> P(i)= poly(x(1:i),"x"); ← La base des polynômes pour la formule de Newton
-->end
-->P=[1;P]
P =
! 1 !
! !
! 5 + x !
! !
! 2 !
! 12.5 + 7.5x + x !
! !
! 2 3 !
! 12.5x + 7.5x + x !
! !
! 2 3 4 !
! - 31.25x - 6.25x + 5x + x !
--> ← On utilise la formule de récursion en conservant les
--> ← premiers termes de chaque colonnes qui seront les coefficients du polynôme
-->col=F;
-->coefP= col(1)*ones(n-1,1);
-->for k=1:n-1
--> col= col(2:$) - col(1:$-1);
--> col= col0./ (x((1+k):$)-x(1:$-k));
--> coefP(k+1)=col(1);
-->end
-->Pn = coefP'*P; ← Le polynôme dflinterpolation
-->nr=200;
-->xr=linspace(-5,5,nr)';
-->yr=f(xr);
-->yp=horner(Pn,xr);
-->pause;xbasc();
plot2d1("onn",xr,[yr,yp])
plot2d(x,F,-2); ← Voir figure 4
-->clear P;
-->for i=1:n-1
--> P(i)= poly(x(1:i),"x"); ← La base des polynômes pour la formule de Newton
-->end
-->P=[1;P]
P =
! 1 !
! !
! 5 + x !
! !
! 2 !
! 12.5 + 7.5x + x !
! !
! 2 3 !
! 12.5x + 7.5x + x !
! !
! 2 3 4 !
! - 31.25x - 6.25x + 5x + x !
--> ← On utilise la formule de récursion en conservant les
--> ← premiers termes de chaque colonnes qui seront les coefficients du polynôme
-->col=F;
-->coefP= col(1)*ones(n-1,1);
-->for k=1:n-1
--> col= col(2:$) - col(1:$-1);
--> col= col0./ (x((1+k):$)-x(1:$-k));
--> coefP(k+1)=col(1);
-->end
-->Pn = coefP'*P; ← Le polynôme dflinterpolation
-->nr=200;
-->xr=linspace(-5,5,nr)';
-->yr=f(xr);
-->yp=horner(Pn,xr);
-->pause;xbasc();
plot2d1("onn",xr,[yr,yp])
plot2d(x,F,-2); ← Voir figure 4
On notera que pour n grand, une évaluation numérique des valeurs du polynôme obtenu par la
formule d’interpolation de Newton par la fonction horner donne de meilleurs résultats que la
même évaluation à partir du polynôme d’interpolation de Lagrange (utiliser la fonction
1∕(1 + x2))
Le programme suivant montre l’aspect séquentiel de la construction par différence divisées.
L’utilisateur rentre les points uns à uns en cliquant, le polynôme d’interpolation est mis à jours
séquentiellement et un graphe est dessiné.
-->function Pplot(a,b,npts,P)
--> xr=linspace(a,b,npts)';
--> yp=horner(P,xr);
--> plot2d1("onn",xr,yp,1,"000")
-->endfunction
-->P=[1];
-->x=[];F=[];
-->while %t
--> plot2d([],[],0,rect=[0,0,1,1])
--> if x<>[]
--> plot2d(x,F,-2,"000");
--> end
--> [but,xnew,fnew]=xclick();
--> xbasc();
--> if but==2 then ; break;end
--> x=[x;xnew];
--> F=[F;fnew];
--> if size(x,'*') <> 1 ;
--> P($+1)= poly(x(1:$-1),"x");
--> [m,n]=size(mat);
--> mat=[mat,zeros(m,1);zeros(1,n+1)];
--> mat(n+1,1)=F($);
--> for j=2:n+1
--> mat(n+1,j)= (mat(n+1,j-1)-mat(n,j-1))/(x(n+1)-x(n+1-j+1));
--> end
--> Pn = diag(mat)'*P;
--> else
--> mat=[F];
--> Pn = F;
--> end
--> Pplot(0,1,100,Pn);
-->end
5 Fonction de Lebesgue, points de Tchebychev
On regarde dans ce paragraphe le comportement de ω(x) = 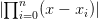 sur l’intervalle [−1, 1]
en fonction du choix des points xi. On regarde le cas des points régulièrement espacés et le cas des
points de Tchebychev :
sur l’intervalle [−1, 1]
en fonction du choix des points xi. On regarde le cas des points régulièrement espacés et le cas des
points de Tchebychev :
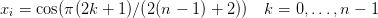 | (10) |
On fait de même pour la fonction de Lebesgue :
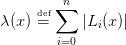 | (11) |
-->n=10;
-->x=linspace(-1,1,n)'; ← Les points dflinterpolation régulièrement espacés
-->xcheb= cos( %pi*(2*(0:n-1)+1)/(2*(n-1)+2)); ← Les points de Tchebychev
-->w=poly(x,"x"); ← Le polynôme 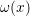 pour les points régulièrement espacés
-->wcheb=poly(xcheb,"x") ← Le polynôme
pour les points régulièrement espacés
-->wcheb=poly(xcheb,"x") ← Le polynôme 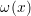 pour les points de Tchebychev
wcheb =
2 3
- 0.0019531 - 2.408D-17x + 0.0976562x + 4.341D-16x
4 5 6 7
- 0.78125x - 6.767D-16x + 2.1875x + 3.761D-15x
8 9 10
- 2.5x - 1.110D-16x + x
-->nr=200;
-->xr=linspace(-1,1,nr)';
-->yr=abs(horner(w,xr));
-->yp=abs(horner(wcheb,xr));
-->xbasc();
-->plot2d1("onn",xr,[yr,yp]) ← Voir figure 5
-->clear P;
-->for i=1:n
--> y=x; y(i)=[]; P(i)= poly(y,"x"); P(i)= P(i)/horner(P(i),x(i));
-->end
-->clear P1;
-->for i=1:n
--> y=xcheb; y(i)=[]; P1(i)= poly(y,"x"); P1(i)= P1(i)/horner(P1(i),xcheb(i));
-->end
-->function y=lebesgue(x,P) ← La fonction de Lebesgue
--> y=abs(horner(P,x)); y=sum(y,'r');
-->endfunction
-->nr=200;
-->xr=linspace(-1,1,nr);
-->yr=lebesgue(xr,P);
-->yrcheb=lebesgue(xr,P1);
-->pause;xbasc();
plot2d1("onn",xr',[yr;yrcheb]') ← Voir figure 6
pour les points de Tchebychev
wcheb =
2 3
- 0.0019531 - 2.408D-17x + 0.0976562x + 4.341D-16x
4 5 6 7
- 0.78125x - 6.767D-16x + 2.1875x + 3.761D-15x
8 9 10
- 2.5x - 1.110D-16x + x
-->nr=200;
-->xr=linspace(-1,1,nr)';
-->yr=abs(horner(w,xr));
-->yp=abs(horner(wcheb,xr));
-->xbasc();
-->plot2d1("onn",xr,[yr,yp]) ← Voir figure 5
-->clear P;
-->for i=1:n
--> y=x; y(i)=[]; P(i)= poly(y,"x"); P(i)= P(i)/horner(P(i),x(i));
-->end
-->clear P1;
-->for i=1:n
--> y=xcheb; y(i)=[]; P1(i)= poly(y,"x"); P1(i)= P1(i)/horner(P1(i),xcheb(i));
-->end
-->function y=lebesgue(x,P) ← La fonction de Lebesgue
--> y=abs(horner(P,x)); y=sum(y,'r');
-->endfunction
-->nr=200;
-->xr=linspace(-1,1,nr);
-->yr=lebesgue(xr,P);
-->yrcheb=lebesgue(xr,P1);
-->pause;xbasc();
plot2d1("onn",xr',[yr;yrcheb]') ← Voir figure 6
6 Approximation en norme L∞ polynômes de Bernstein
On cherche ici à approximer une fonction sur [0, 1] par les polynômes de Bernstein :
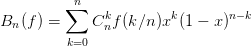 | (12) |
On utilise le fait que pour x fixé dans [0, 1] les coefficients Cnkxk(1 − x)n−k sont les
probabilités d’une loi binomiale. La fonction Scilab binomial(x,n-1) est utilisée pour leurs
calculs.
-->function y=f(x)
--> y=sin(5*%pi*x)0./ (1+ 25*x.*x)
-->endfunction
-->nr=200;
-->xr=linspace(0,1,nr)';
← Les valeurs de  pour lesquelles on veut évaluer
pour lesquelles on veut évaluer 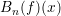 -->yr=f(xr);
-->for n=5:20:200
--> x=linspace(0,1,n)';
--> F=f(x);
--> Bnf=ones(xr);
--> for i=1:nr
--> Bnf(i) = binomial(xr(i),n-1)* F;
← Valeur du
-->yr=f(xr);
-->for n=5:20:200
--> x=linspace(0,1,n)';
--> F=f(x);
--> Bnf=ones(xr);
--> for i=1:nr
--> Bnf(i) = binomial(xr(i),n-1)* F;
← Valeur du  -ième polynôme de Bernstein pour x=xr(i)
--> end
--> plot2d1("onn",xr,[yr,Bnf]); ← Voir figure 7
-->end
-ième polynôme de Bernstein pour x=xr(i)
--> end
--> plot2d1("onn",xr,[yr,Bnf]); ← Voir figure 7
-->end
On retrouve de façon directe avec la construction des polynômes de Bernstein la densité pour
la norme infinie des polynômes dans les fonction continues sur [−1, 1].
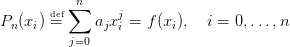
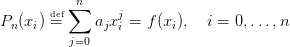
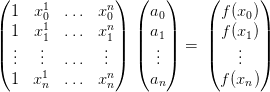
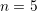 ,
, 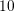 et
et 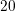
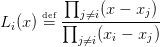
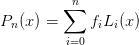

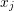 en retirant le
en retirant le  -ème
-ème
 -ème polynôme de Lagrange
-ème polynôme de Lagrange
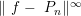
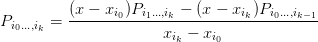
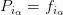
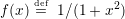
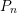
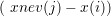
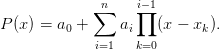

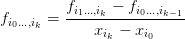
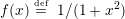
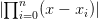 sur l’intervalle [−1, 1]
en fonction du choix des points xi. On regarde le cas des points régulièrement espacés et le cas des
points de Tchebychev :
sur l’intervalle [−1, 1]
en fonction du choix des points xi. On regarde le cas des points régulièrement espacés et le cas des
points de Tchebychev :
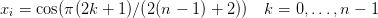
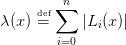
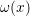 pour les points régulièrement espacés
pour les points régulièrement espacés
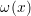 pour les points de Tchebychev
pour les points de Tchebychev
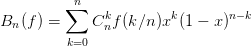
 pour lesquelles on veut évaluer
pour lesquelles on veut évaluer 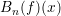
 -ième polynôme de Bernstein pour x=xr(i)
-ième polynôme de Bernstein pour x=xr(i)