Automatique
Les questions

Contents

1 Macros générales utilisées

1.1 boucle

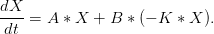
A quoi ça sert ? Et bien boucle permet de tracer des trajectoires pour un système non linéaire bouclé. Il trace alors la trajectoire du système, la trajectoire des observations, l’écart entre ces 2 trajectoires, et la commande. Et on peut même rajouter du bruit. Le TD concernant le modèle (biologique) de compétition utilise cette macro et permet de mieux se rendre compte de ce que fait cette macro.

boucle prend comme arguments uniquement la fonction fct, et éventuellement la variance du bruit que l’on souhaite ajouter. Mais en fait, boucle fait appel à un grand nombre de variables globales, qui sont : le point d’équilibre xe, la commande ue, les matrices du système linéarisé autour du point d’équilibre f, g (la matrice de commande) et h (la matrice des mesures), et les matrices de gain de commande k et d’observation l. On retrouve les mêmes variables globales que pour obscont1.

1.2 contr

Cette macro renvoie la dimension et les vecteurs de base du sous-espace controlable de la paire (A,B) grâce à l’appel [n,base]=contr(A,B).

Rappelons que si on note V=U(:,1:n), alors V’*A*V et V’*B donnent la partie controlable de la paire (A,B).

1.3 obscont1

Cette macro renvoie une fonction corrrespondant à une version bouclée du système qu’on lui donne en unique argument. Mais l’unicité de l’argument cache le fait que obscont1 fait appel à un grand nombre de variables globales, qui sont : le point d’équilibre xe, la commande ue, les matrices du système linéarisé autour du point d’équilibre f, g (la matrice de commande) et h (la matrice des mesures), et les matrices de gain de commande k et d’observation l.

L’appel se fait par [fctboucle]=obscont1(fct).

1.4 ppol

Cette macro permet de placer les pôles, c’est-à-dire qu’à partir des arguments f, g et pole, elle renvoie la matrice k telle que f-g*k ait pole pour spectre. Ce qui permet donc de trouver la matrice de gain de commande à partir des pôles désirés.

L’appel est donc : k=ppol(f,g,pole).

Notons que pour placer les pôles d’un observateur, il faut utiliser la transposition. En effet, on a tout simplement l=ppol(f’,h’,pole)’, en notant ’ la transposition et h la matrice des mesures.

2 Systèmes dynamiques linéaires et stabilité

2.1 Système linéaire avec feedback linéaire

2.1.1 De quoi s’agit-il ?

On a vu qu’avec un système dynamique linéaire, le point origine 0 peut ne pas être asymptotiquement stable. Nous allons essayer de le rendre asymptotiquement stable à l’aide d’une commande en feedback u = −K ∗ X qui ramènera le système vers le point origine.
On utilise donc le système dynamique

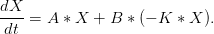(1)

Les paramètres de ce système ont sous Scilab les noms A_lincom, B_lincom et K_lincom.

2.1.2 Simulation

Nous allons utiliser la macro lincom. Comme précédemment, son chargement en mémoire se fait à l’aide de la fonction linsys(), et l’initialisation des paramètres se fait grâce à lin_init().

1. Prendre un gain nul (K=[0 0]). Visualiser ainsi le champ de vecteurs original. Quelle est la nature du point d’équilibre 0 ?
2. Modifier K de sorte que le point 0 devienne asymptotiquement stable. Visualiser le champ de vecteurs obtenu.
3. Donner un moyen théorique de trouver des matrices de gain K telles que 0 soit un point asymptotiquement stable du système linéaire bouclé.
4. Reprendre ces questions avec la matrice A =

2.2 Un modèle de compétition bouclé

Nous avons vu dans la partie “Systèmes Dynamiques” un modèle de compétition. Nous allons à présent compléter la simulation en bouclant ce système.

2.2.1 Rappel du modèle considéré

On modélise la dynamique de deux populations vivant sur une même ressource par un système d’équations :

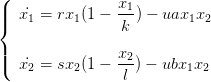(2)

où 1/u est le niveau de ressources et r,s,k,l,a,b des paramètres que l’on peut faire varier (attention : ces paramètres sont notés r_compet, s_compet, etc... sous Scilab. Seule u possède le même nom u).

2.2.2 Simulation du système bouclé

1. Si cela n’a pas déjà été fait précédemment, définir les matrices f et g qui correspondent au linéarisé tangent du système au point d’équilibre. Elles s’obtiennent par la commande [f,g,complin]=tangent(’compet’,equilcom(ue),ue), où equilcom est une fonction renvoyant les coordonnées du point d’équilibre pour une commande u donnée.
2. Définir les variables globales xe (contenant les coordonnées du point d’équilibre), ue (ressource) et h=[1,0].
3. Choisissons à présent les matrices de gain de la commande et de l’observateur. Nous allons utiliser la commande ppol. Nous prendrons des pôles de l’ordre de -1/100. Calculer la matrice de gain de la commande en tapant k=ppol(f,g,pole), où pole est un vecteur colonne. La valeur renvoyée pour k est telle que f-g*k ait un spectre égal au vecteur pole.
   En ce qui concerne l’observateur, c’est un peu moins direct. En effet, les pôles que nous voulons correspondent au spectre de la matrice f-l*h. Pour pouvoir utiliser ppol, nous allons donc utiliser la transposée de cette matrice (on retrouve le phénomène de dualité entre commande et observateur) : l’=ppol(f’,h’,pole).
   Les matrices k et l introduites ici ne doivent pas être confondues avec les paramètres k et l (k_compet et l_compet).
4. Taper boucle(’bcomp’) pour visualiser le système (non linéaire) bouclé avec les matrices k et l. On choisira n=200 et pas=10. Observer l’effet des non-linéarités suivant le choix du point initial x0.
5. Bruiter la sortie en tapant boucle(’bcomp’,0.5) (0.5 est la variance du bruit introduit). Qu’observe-t-on ?
6. Changer les valeurs des gains de la commande et de l’observateur. Reprendre les questions ci-dessus.
7. Il existe une macro permettant de créer un système dynamique observé-controlé à partir d’un système donné : obscont1. Il suffit de taper obscont1(’compet’) (après avoir défini xe, ue, f, g, h, l et k). On peut alors utiliser boucle(compet1) à la place de boucle(’bcomp’). On notera que la version bcomp, précompilée en Fortran, est bien plus rapide que compet1, interprété par Scilab.
8. Pour finir, tester la fonction [f1,f2]=test_d(ue), qui renvoie en f1 la partie linéaire du système bouclé par observateur contrôleur calculée par linéarisation, et en f2 la valeur théorique.