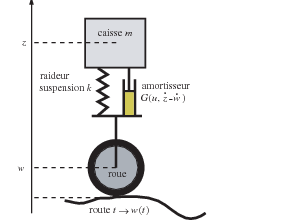
On considère un quart de véhicule constitué d’une roue, de son ressort et de son amortisseur. L’amortisseur hydraulique a un coefficient d’amortissement variable que l’on peut commander. Un tel système de suspension est appelé semi-actif 1 . Il est muni d’une électro-vanne permettant de faire varier sa pression d’huile et l’électro-vanne est pilotée par la tension électrique appliquée à ses bornes. Notons que ce dernier peut reproduire ou atténuer le mouvement relatif vertical de la roue par rapport à la caisse mais ne peut s’y opposer, contrairement aux systèmes de suspension active.
Le but de ce TP est d’analyser l’influence du profil de route sur le comportement vertical du véhicule et de régler la commande de l’amortisseur. Le quart de véhicule (voir Fig. 1) a pour masse m = 215 kg, et se trouve, au repos, à une hauteur h = 0, 8 m du sol. Le ressort (vertical) a pour raideur k = 50000 N/m et la force G(u,v) générée par l’amortisseur en fonction de la vitesse verticale relative vr du véhicule par rapport à la route est donnée (voir Fig. 2) par
![[ 2 ( ( a u + b )) ]
G (u,vr) = μvr + (a0u + b0)--arctan vr -1-----1 ⋅
π[ ( a0u + b)0 ]
⋅ (1 +-α-)+ (1-−-α-)- 2-arctan(vr )
2 2 π β](Suspension1x.png) | (1) |
avec μ = 666 Ns/m, a0 = 600, b0 = 700, a1 = 7000, b1 = 26000, α = 155∕170, β = 0.5, pour
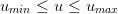
On note w(x) la hauteur (en m) du moyeu central de la roue pour la position horizontale x. On
suppose pour simplifier que la dynamique du pneu est négligée et que w est donnée et représente
le profil de la route. On note ẇ = 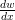 V (t) la vitesse verticale de la route, où V (t) est la vitesse
horizontale du véhicule. On rappelle que g = 9.81 N/kg.
V (t) la vitesse verticale de la route, où V (t) est la vitesse
horizontale du véhicule. On rappelle que g = 9.81 N/kg.
La dynamique verticale de l’ensemble est décrite par
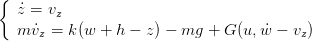 | (2) |
Les conditions intiales sont données par z0 = h−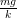 (hauteur de caisse initiale, en m) et v0 = 0
(vitesse verticale initiale en m/s).
(hauteur de caisse initiale, en m) et v0 = 0
(vitesse verticale initiale en m/s).
Question 1 Pour un profil de route horizontal (w(x) = 0), montrer que l’ensemble des points d’équilibre du système (2) est réduit à un unique point, que l’on calculera, et que ce dernier ne dépend pas de la commande u.
Question 2 Calculer le linéarisé tangent de (2) à l’équilibre pour u = umin et u = umax et ses valeurs propres. Que peut-on conclure sur la stabilité du système ?
Question 3 Le système linéarisé tangent à l’équilibre est-il commandable au premier ordre ? Le système non linéaire (2) est-il localement accessible ?
Question 4 Lancer le programme de simulation en boucle ouverte suspbo.sce pour une montée de trottoir (choice==2)(2 d’une hauteur H = 0.05 m puis H = 0.07 m à la vitesse horizontale V = 10 m/s, avec successivement u = umin, u = 0, u = 1, u = umax. Que constatez-vous ? Analyser le comportement du véhicule pendant et après la montée. Comment interpréter les oscillations en regard du calcul des valeurs propres calculées à la question 1.2 ?
Question 5 Même question pour une descente de trottoir avec les mêmes valeurs de H et u (choice==3).
Question 6 On considère maintenant un roulage (choice==1, toujours à vitesse horizontale V = 10 m/s, sur route pavée, modélisée par une sinusoïde d’amplitude Hp = 0.02 m et de période 0.1 s (qui correspond à des pavés d’une hauteur de 2Hp = 0.02 m et d’une longueur de 0.1 m). Analyser le comportement du véhicule pour les périodes 0.015 s, 0.1 s, 0.5 s, 1 s, 5 s et 10 s. Que remarque-t-on ? Comment l’analyse de la question 1.2 peut-elle aider à prédire le comportement du véhicule à haute fréquence ?
On veut essayer d’améliorer le comportement du véhicule tant du point de vue du confort (atténuation de l’accélération et de la vitesse verticales transmises des roues à la caisse) que de la sécurité (limitation des rebonds pouvant entraîner la perte d’adhérence de la roue au sol). La loi de commande que nous étudions ici est appelée en américain skyhook (accrochage au ciel) et peut s’expliquer de façon imagée par la Fig. 3.
Plus précisément, on veut que la force de frottement produite par l’amortisseur ne dépende pas de la perturbation ẇ, soit, idéalement :
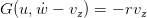 | (3) |
où r > 0, le coefficient de frottement visqueux de l’amortisseur idéal, est arbitraire.
Cependant, l’interprétation géométrique de l’équation (3) à partir de la Fig. 2, montre que (3) n’a de solution que si
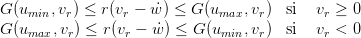 | (4) |
où l’on a posé vr = ẇ − vz. Ainsi,lorsque les inégalités (4) ne sont pas vérifiées, on complète la définition de la commande par u = umin ou u = umax suivant la règle :
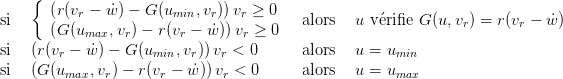 | (5) |
On va maintenant régler le gain r dans les 3 situations précédentes en utilisant le programme “suspbf.sce” de simulation en boucle fermée.
Question 7 Quel doit être l’ordre de grandeur de r pour que (4) puisse avoir des solutions ?
Question 8 Dans le cas de la montée de trottoir, affiner par simulation la valeur de r pour ne plus avoir de rebond en fin de montée pour des hauteurs h ≤ 0.07 m.
Question 9 Vérifier que ce réglage donne le même résultat dans le cas de la descente du trottoir.
Question 10 Que donne ce réglage pour la route pavée de la question 1.6 ? Doit-on encore affiner le réglage de r ? Expliquer.
Question 11 Pour réaliser en temps réel cette loi de commande, de quelles mesures doit-on disposer et grâce à quels capteurs ? Conclure sur les possibilités d’amélioration de la suspension passive.