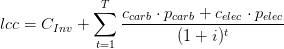
Avant de commencer, créer un fichier optval.sce commençant par:
| Classique | Efficace | Electrique | |
| Cout ($) | 16 500 | 22 000 | 29 000 |
| Consommation (10−6 tep/km) | 70.4 | 52.9 | 15.4 |
| Part de marché à l’année de référence (%) | 88 | 10 | 2 |
On classe les voitures européennes selon trois grands types ou technologies: “classique”,“efficace” et “électrique”. On résume leurs caractéristiques dans le tableau 1. A l’année de référence, l’essence coute 1 700 $/tep et l’électricité coute 2 000 $/tep. Les automobilistes gardent en moyenne 8 ans leur voiture, et parcourent 14 000 km par an.
Question 1 Incorporez ces données à optval.sce.
Les notes d’un chercheur mentionnent lcc(j), valeur associée à chaque technologie j et calculée grâce à la relation:
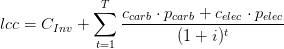 | (1) |
Question 2 Que représente d’après vous lcc pour chaque technologie? Identifiez chaque terme de l’équation (1).
D’après les notes du chercheur, la part de chaque technologie dans le stock d’automobiles msh (pour market share) vérifie
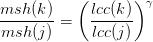 | (2) |
où γ est un nombre négatif qui est fonction de l’homogénéité du marché, et (j,k) représente un couple de technologies.
Question 3 Quelle valeur de gamma pourrait représenter un marché parfaitement homogène, i.e. pour lequel tous les consommateurs ont rigoureusement le même comportement ?
La fonction scilab suivante calcule un lcc kilométrique annualisé. On en parlera tout de même par la suite comme du lcc.
Question 4 Proposez un calcul direct de chaque msh en fonction de tous les lcc, puis complétez la fonction scilab suivante destinée à calculer les parts de marché de chaque technologie. On pourra utiliser la puissance terme à terme .^ et la commande sum.
Les notes du chercheur proposent les valeurs suivantes pour le taux d’actualisation et la variable d’homogénéité du marché.
Question 5 Vérifiez que ces valeurs donnent des résultats proches des parts de marchés constatées (tableau 1).
On s’intéresse au cout moyen annualisé du système automobile :
Question 6 Quel est le cout moyen annualisé du système automobile simulé à l’année de référence?
L’évolution des prix des énergies est difficile à prévoir, notre chercheur ne peut donc pas assoir son analyse sur une prévision unique des prix. Les prévisions consultées par notre chercheur se contredisent: les prix pourraient aussi bien doublés qu’être divisés par deux ! Le chercheur décide de modéliser les prix futurs comme des variables aléatoires log-normales :
Question 7 Pourquoi avoir choisi une représentation log-normale ? Comparez ce que sait notre chercheur sur l’évolution future des prix du carburant et de l’électricité.
Question 8 Calculer, pour chaque couple de prix futurs, les parts de marché de la voiture électrique (VE) et le cout moyen annualisé du système de transport.
Question 9 Calculez et affichez de même la distribution de cost_no_VE, cout annualisé du système automobile lorsque les VE ne sont pas disponibles. On pourra utiliser une astuce pour exclure rapidement le VE, comme:
On suppose que le revenu moyen des automobilistes est de 30 000 $. On suppose que les déplacements automobiles sont contraints et les automobilistes n’y associent aucune utilité. Cette dernière dépend du logarithme du revenu disponible après déplacements automobiles :
Question 10 Commentez la forme fonctionnelle de l’utilite à la lumière du TP Risk and decision. L’objectif est de calculer l’effet de la disponibilité du VE sur l’utilité espérée. Pourquoi a-t-on besoin de connaitre le revenu ?
Question 11 Affichez la distribution d’utilité dans les cas avec et sans VE, en faisant apparaitre l’utilité espérée. Commentez l’effet de la disponibilité des VE sur la distribution de l’utilité.
Le gouvernement propose de financer la création de la filière de production de voitures électriques par une taxe forfaitaire et payée par les automobilistes (à l’image de la vignette automobile). On cherche quel est le montant maximal que l’automobiliste est prêt à payer aujourd’hui pour s’assurer que des VE seront disponibles si nécessaires dans le futur.
Question 12 Calculer le prélèvement maximal que l’on peut ponctionner sur le revenu des automobilistes en échange de la garantie que des voitures électriques seront disponibles dans le futur. Il s’agit de la valeur que l’automobiliste partageant avec notre chercheur les croyances sur les prix futurs de l’énergie accorde à une option sur le véhicule électrique (VE).
Question 13 Comparez la valeur d’option à l’effet des VE sur moyenne du cout du système automobile. Commentez la valeur absolue et le signe de la différence entre ces deux valeurs.
Les bonnes pratiques administratives imposent de s’interesser au cost at risk des projets sur lesquels la puissance publique intervient. On appelle cost at risk au niveau λ du système automobile le cout annualisé x tel que le cout futur du système automobile soit inférieur à x avec une probabilité de 1 − λ.
Question 14 Calculer et comparer le cost at risk au niveau 5% du système automobile lorsque les VE sont disponibles et indisponibles.
| Prix du carbone ($) | 0 | 10 | 30 | 200 |
| Abbatements (GtCO2) | 0 | 0.5 | 1 | 2 |
Il y a 220 millions de véhicules dans le parc. La consommation de carburants s’accompagne d’émissions de CO2: l’électricité contient 400 gCO2/kWh, et les carburants liquides contiennent 2.8 tC02/tep.
Question 15 Complétez la fonction scilab qui calcule les emissions de gaz à effet serre du système automobile, puis calculez les émissions des voitures à l’année de référence.
On s’intéresse aux émissions totales de CO2. Le reste de l’économie (hors système automobile) est responsable de 4.5 GtCO2/an. On souhaite appliquer une taxe carbone pour réduire les émissions de CO2. Notre chercheur connait précisément la réponse du reste de l’économie à une taxe carbone, qui est résumée dans le tableau 2.
Question 16 Complétez la fonction suivante qui calcule les émissions de CO2 du reste de l’économie en fonction du niveau de la taxe. On pourra utiliser la commande interpln.
Notre chercheur est de plus certain que le contenu carbone de l’éléctricité décroit linéairement avec le niveau de la taxe, pour atteindre 0 à 250 $/tCO2:
On souhaite tester la réponse de notre modèle à un prix du carbone. Pour l’instant, on soumet arbitrairement le modèle à des taxes de 0, 10, 30, 60 et 100 $/tCO2, qui seront considérées équiprobables.
Question 17 Calculer, afficher et commmenter la distribution des émissions de gaz à effet de serre totaux, quand le VE est disponible et lorsqu’il ne l’est pas. Pour cela compléter le programme ci-dessous :
Question 18 Que deviennent alors la valeur d’option du VE et les Cost at risk du système automobile?
Plutôt que de faire des scénarios sur le prix futur du CO2, on souhaite contraindre l’économie à réduire de moitié ses émissions. On cherche donc, dans chaque scénario, a appliquer le prix du carbone qui permet d’atteindre cet objectif.
La fonction suivante calcule la plupart des variables de notre modèle. Elle peut être utilisée comme le montrent les exemples ci-dessous pour calculer les variables du modèle ou pour trouver la taxe qui contraint les émissions à un niveau donné.
Question 19 Utiliser les deux formes de cette fonction pour calculer, afficher et comparer la distribution de taxe permettant d’atteindre l’objectif de diviser par deux les émissions de l’économie entière, avec et sans VE disponibles.
Question 20 Calculer la nouvelle valeur d’option du VE et les nouveaux Cost at Risk.