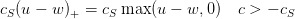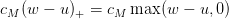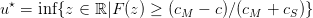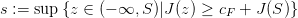Le vendeur de journaux

Jean-Philippe Chancelier
(last modification date: March 23, 2018)
Version pdf de ce document
Version sans bandeaux

1 Le problème du vendeur de journaux (à une période de temps)

Contents

1 Le problème du vendeur de journaux (à une période de temps)
 1.1 La demande aléatoire
 1.2 On utilise tout d’abord la distribution binomiale
 1.3 On utilise maintenant une loi discrète à 3 valeurs
 1.4 La loi du coût
 1.5 Un problème linéaire
 1.6 Une stratégie [s,S]
 1.7 Correction

1 Le problème du vendeur de journaux (à une période de temps)

1.1 La demande aléatoire

On veut faire tourner le même code pour plusieurs lois distinctes qui seront des lois discrètes. On utiliser un select en Scicoslab qui permettra de choisir la loi utilisée pour les calculs.

  // la proba a construire est stockée dans un vecteur ligne
  test=1,// pour selectionner la loi à utiliser
  
  select test
    case 1 then
     // On utilise ici une loi binomiale de paramètres (n,p)
     // pdf("bin",x,n,p) = n!/x!(n-x)! p^x (1-p)^n-x
     // titre: chaine de caratères décrivant la loi
     // wi: vecteur contenant les valeurs possibles
     // pi: vecteur contenant les probabilités associées
     // mu: calculer la moyenne de la loi
     N=100000;
     // W: un echantillon de taille N de la loi considérée
     n=100;
     p=0.5;
     titre=sprintf("loi binomiale(%d,%5.2f)",n,p);
     wi=0:n;// les valeurs possibles
     pi=binomial(p,n);// les probabilités associées
     mu=n*p;// moyenne de la binomiale
     mu1=pi*wi';// vérification
     if abs(mu-mu1) > 1.E-8 then pause ;end
     // un echantillong de taille N
     N=100000;
     W=grand(1,N,"bin",n,p);
    case 2 then
     // une loi discrète sur trois valeurs
     // par exemple une loi uniforme sur les trois valeurs
     wi=[30,50,80];
     //pi=[ <<A-FAIRE>> ];
     titre=sprintf("loi discrète sur %d valeurs",size(wi,'*'));
     //mu=  <<A-FAIRE>> ];
     // un echantillong de taille N
     N=100000;
     // <<A-FAIRE>>: expliquer pourquoi avec une matrice de transition
     // dont toutes les lignes sont semblalbles on simule des v.a indépendantes.
     // On va donc utiliser grand avec l'option Markov
     P=[],for i=1:length(pi) do P=[P;pi];end
     // <<A-FAIRE>>: recalculer P de façon vectorielle
     Y=grand(N,'markov',P,1);
     // Y prends ses valeurs dans [1,length(pi)]
     // Il faut construire un vecteur W tel que
     // W(i) soit 30 si Y(i)==1, 50 si  Y(i)==2, 80 si Y(i)==3
     // code cela de la façon la plus économique possible !
     //W = <<A-FAIRE>> Y
    case 3 then
     // loi de Poisson
     // On choisit une loi de poisson de paramètre mu
     n=100;
     p=0.5;
     mu=n*p;// moyenne de la loi de poisson
     wi=0:n;
     // pi=[ <<A-FAIRE>> ];
     titre=sprintf("loi de Poisson de paramètre %f",mu);
     N=100000;
     // W=grand(<<A-FAIRE>>)
  end

Question 1 Pour chacune des lois proposées faites un graphique de la fonction de répartitions de la loi et un graphique de la densité de la loi

On pourra utiliser le squelette de programme suivant.

  // graphique de la loi de la demande et de sa 
  // fonction de répartition 
  
  if %t then
    function graphique_loi(titre,valeurs,probas)
      // dessin de la loi discrete et de sa fonction de 
      // repartition. 
      // la loi discrete se caractérise par le vecteur valeurs 
      // et le vecteur probas de même taille.
  
      xset('window',1);
      xbasc();
      // bornes du graphique: rect=[xmin,ymin,xmax,ymax]
      rect=[0,0,max(valeurs)+10,min(max(probas)+0.2,1)]
      plot2d3(valeurs,probas,rect = rect,style = 2);
      xtitle(titre);
      xset('window',2);
      xbasc();
      // dessin de la fonction de repartition 
      // plot2d2: tracé en escalier 
      rect=[0,0,max(valeurs)+10,1.1]
      // le vecteur repart doit contenir la valeur de la fonction 
      // de repartition associée aux points valeurs 
      // (On pourra utiliser la fonction cumsum).
      //A-FAIRE:  repart=[<<A-FAIRE>>];
      plot2d2([0,valeurs],[0,repart],rect = rect,style = 2)
      // plot2d: tracé des points gauches 
      plot2d(valeurs,repart,rect = rect,style = -3)
      xtitle(sprintf('Fonction de repartition de la %s',titre));
    endfunction
  
    graphique_loi(titre,wi,pi);
    xclick();// il faut cliquer sur le graphique pour continuer
  end

1.2 On utilise tout d’abord la distribution binomiale

On se place dans le cas test=1.

Question 2 Écrire une fonction Scicoslab qui calcule j(u,w) puis une fonction qui calcule J(u). Faire un graphique avec les valeurs proposées des constantes et calculer le nombre de journaux qu’il faut commander

  // parametres de la fonction cout 
  
  c=10,cm=20,cs=5;
  
  // la fonction cout j(u,w)
  
  function y=j(u,w)
    //A-FAIRE y= <<A-FAIRE>>
  endfunction
  
  // La fonction J(u) pour la loi binomiale en 
  // utilisant wi et pi
  
  function y=J(u)
    //A-FAIRE y= <<A-FAIRE>>
  endfunction
  
  // graphique de la fonction J(u) et recherche du minimum
  
  if %t then
    U=-10:100;
    //Ju: valeur de J(u) quand U prends les valeurs -10:100
    Ju=[];for u=U do
      //A-FAIRE      <<A-FAIRE>>;
    end
    xset('window',1);xbasc();
    plot2d(U,Ju,style = 2);
    xtitle("La fonction J");
    // recherche du minimum de la fonction J et de son argmin 
    // La fonction min permet cela.
    //A-FAIRE [Jmin,kmin]=  <<A-FAIRE>>
    //A-FAIRE uopt= U(<<A-FAIRE>>);
    printf("Nombre optimal de journaux a commander %f\n",uopt);
    printf("Moyenne de la demande %f\n",mu);
    plot2d(uopt,m,style = -4);// dessin
    plot2d3(uopt,m);
    xclick();
  end

Question 3 Vérifier sur un graphique que le nombre de journaux optimal à commander s’obtient par la formule :

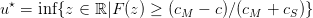u ⋆ = inf{z ∈ ℝ |F (z) ≥ (c − c)∕ (c + c )} M M S
(1)

  // graphique de la fonction J(u) et recherche du minimum
  // en utilisant la fonction F(z) 
  
  if %t then
    xset('window',1);
    xbasc();
    fstar=(cm-c)/(cm+cs);
    plot2d([0,wi],fstar*ones([0,wi]),rect = [0,0,max(wi)+10,1.1],style = 1);
    // La fonction de repartition 
    Fv=cumsum(pi)
    plot2d2([0,wi],[0,Fv],rect = [0,0,max(wi)+10,1.1],style = 2);
    // Calculer kopt en utilisant le resultat vu dans les slides.
    //A-FAIRE <<A-FAIRE>>
    kopt=plot2d(wi(kopt),Fv(kopt),rect = [0,0,max(wi)+10,1.1],style = -4);
    xclick()
  end

1.3 On utilise maintenant une loi discrète à 3 valeurs

Dans le cas précédent, on trouve que le nombre de journaux optimal à commander est très voisin de la moyenne de la demande. On cherche ici à construire un exemple ou les deux nombres seront franchement différents.

Question 4 Reprendre ce qui précède, en vous plaçant maintenant dans le cas test=2 et chercher à caler des valeurs des probabilités qui permettent d’obtenir le résultat souhaité.

1.4 La loi du coût

Question 5 Dans les cas test=1 et test=2, faites un graphique de la loi du coût pour diverses valeurs de la commande u. On procédera de deux façons différentes

  // graphique de la loi du cout en fonction du paramètre u 
  
  if %t then
    function graphique_loi_cout(u,wi,pi)
      xbasc();
      xset('window',1);
      // valeurs possible des couts avec eventuelle répétition
      //A-FAIRE   ji1 = <<A-FAIRE>>
      // on trouve les valeurs non répétées avec la fonction unique 
      ji=unique(ji1);
      // on claule les probas associées 
      pji=0*ji;
      for i=1:size(ji,'*') do
        I=find(ji1==ji(i));// permet de savoir quels w ont contribué a ji(i)
        //A-FAIRE pji(i)= sum(<<A-FAIRE>>)
      end
      moy=pji*ji';
      vmax=min(max(pji+0.2),1);
      xmax=2000;
      plot2d3(ji,pji,rect = [0,0,xmax,vmax],style = 2);
      plot2d3(moy,vmax,rect = [0,0,xmax,vmax],style = 1);
      xtitle(sprintf('Loi de la fonction cout pour u=%f',u))
    endfunction
  
    // graphique de la loi du cout pour diverses valeurs de u 
    xset('window',1);
    xbasc();
    for u=[0:10:100] do
      graphique_loi_cout(u,wi,pi);
      xclick();
    end
  end
  
  // graphique de la loi du cout suivant le paramètre u 
  // On dessine la loi empirique obtenue avec des tirages 
  // montecarlo de la demande (On rappelle que c'est les W 
  // qu'on aconstruit au début du TP).
  
  if %t then
    function graphique_loi_cout_mc(u,Wmc)
      xbasc();
      xset('window',1);
      // valeurs possible des couts obtenus à partir 
      // des tirages Wmc
      //A-FAIRE Jv = <<A-FAIRE>>
      // On veut trouver les valeurs distinctes contenues dans le 
      // le vecteur Jv 
      ji=unique(Jv);
      // Calculer la proba associée à chacune de ces valeurs distinctes.
      //A-FAIRE pji= <<A-FAIRE>>
      moy=mean(Jv);
      vmax=min(max(pji+0.2),1);
      xmax=2000;
      plot2d3(ji,pji,rect = [0,0,xmax,vmax],style = 2);
      plot2d3(moy,vmax,rect = [0,0,xmax,vmax],style = 1);
      xtitle(sprintf('Loi de la fonction cout pour u=%f',u))
    endfunction
  
    // graphique d'une approximation Monte-Carlo de la loi du cout 
    // pour diverses valeurs de u 
  
    for u=[0:10:100] do
      // Les W sont les tirages Monte-Carlo
      graphique_loi_cout_mc(u,W);
      xclick();
    end
  end

1.5 Un problème linéaire

Question 6 En utilisant la présentation faite en cours, construire un problème linéaire dont la solution permet de calculer le nombre de journaux optimal à commander

  // On regarde ce problème comme un problème linéaire 
  // on introduit de nouvelles variables z et w pour linéariser les deux max 
  // cout = c*u + sum_s cs*pi_s* z_s +cm*y_s*w_s 
  // q in[10,100]
  // z_s >= q - x_s 
  // w_s >= x_s -q 
  // var=[q;z;w] 
  
  function [A,B,C,lb,ub]=linprog_vendeur(wi,pi)
    m=size(pi,'*');
    // A*var <= B
    //A-FAIRE  A= <<A-FAIRE>>
    //A-FAIRE  B= <<A-FAIRE>>
    // le cout (vecteur colonne)
    //A-FAIRE  C= <<A-FAIRE>>
    // bornes min et max 
    lb=[0;zeros(m,1);zeros(m,1)];
    ub=[100;%inf*ones(m,1);%inf*ones(m,1)];
  endfunction
  
  if %t then
    [A,B,C,lb,ub]=linprog_vendeur();
    [varopt,lagr,fopt]=linpro(C,A,B,lb,ub);
    usharp=varopt(1);
  end

1.6 Une stratégie [s,S]

On regarde maintenant un cas ou le vendeur à déjà des journaux et ou il paye un coup fixe si il commande des journaux. On cherche à retrouver ici le fait que la stratégie optimale est de la forme [s,S].

Question 7 On se placera dans le cas test=1. Calculer le nombre optimal de journaux à commander suivant la valeur du stock initial. Vérifier que la stratégie est bien de la forme [s,S]: on remonte le stock au niveau S si il est inférieur à s et on ne fait rien sinon. Calculer s par la formule

s := sup {z ∈ (− ∞, S)|J(z) ≥ cF + J(S )}

  cf=200;// coût fixe 
  
  function y=Jtilde(u,x)
    y=cf*(u > 0)+J(u+x)-c*x
  endfunction
  
  xuopt=[];
  // valeur possible pour x 
  xv=0:1:2*max(wi);
  U=0:1:2*max(wi);
  for x0=xv do
    //A-FAIRE  Jtildeu= <<A-FAIRE>>// valeurs correspondantes pour Jtilde
    //A-FAIRE  uopt = <<A-FAIRE>>// le u optimal pour x0 
    xuopt=[xuopt,uopt];// on garde tous les u optimaux 
  end
  
  // trouver l'indice ou la quantité commandée devient nulle
  //A-FAIRE I=find(<<A-FAIRE>>)
  // cela permet de trouver s 
  //A-FAIRE s=<<A-FAIRE>>
  
  // vérifier que la stratégie optimale est [s,S];
  
  xset('window',1);
  xbasc();
  plot2d2(xv,xuopt,style = 2);// les couples x, u optimal 
  
  // retrouver s avec la formule du cours, 
  // S=uopt est connu on sait que c'est le uopt qui minimise J
  for x=0:2*max(wi) do
    //A-FAIRE if <<A-FAIRE>> then kopt=<<A-FAIRE>>;break;end
  end
  s=kopt;

1.7 Correction

  // -*- Mode:scilab -*- 
  
  // Vendeur de journaux 
  // cout = c*q +csE[(q-D)^+] + cm*E[(D-q)^+];
  
  // g(q) s'écrit aussi 
  // g(q) = cm*E[D] + int_0^q ((c-cm) + (cm+cs)F(z)dz 
  // On regarde le cout pour diverses lois de probas pour D 
  
  // On utilise ici une loi binomiale de paramètres (n,p) 
  // pdf("bin",x,n,p) = n!/x!(n-x)! p^x (1-p)^n-x 
  
  test=2;
  
  select test
    case 1 then
     // On utilise ici une loi binomiale de paramètres (n,p) 
     // pdf("bin",x,n,p) = n!/x!(n-x)! p^x (1-p)^n-x 
     n=100;
     p=0.5;
     titre=sprintf("loi binomiale(%d,%5.2f)",n,p);
     wi=0:n;// les valeurs possibles 
     pi=binomial(p,n);// les probabilités associées 
     mu=n*p;// moyenne de la binomiale 
     mu1=pi*wi';// vérification 
     if abs(mu-mu1) > 1.E-8 then pause ;end
     // un echantillong de taille N
     N=100000;
     W=grand(1,N,"bin",n,p);
    case 2 then
     // une loi discrète 
     wi=[30,50,80];
     pi=[1/2,1/4,1/4];
     titre=sprintf("loi discrète sur %d valeurs",size(wi,'*'));
     mu=pi*wi';// la moyenne
     // un echantillong de taille N
     N=100000;
     P=ones(size(wi,'*'),1)*pi;
     Y=grand(N,'markov',P,1);
     W=wi(Y);
    case 3 then
     // loi de Poisson
     // On choisit une loi de poisson de paramètre mu 
     n=100;
     p=0.5;
     mu=n*p;
     wi=0:n;
     pi=(mu .^wi*exp(-mu)) ./gamma(wi+1);
     // 
     titre=sprintf("loi de Poisson de paramètre %f",mu);
     N=100000;
     W=grand(1,N,'poi',mu);
  end
  
  // graphique de la loi de la demande et de sa 
  // fonction de répartition 
  
  if %t then
    function graphique_loi(titre,valeurs,probas)
      // dessin de la loi 
      xset('window',1);
      xbasc();
      plot2d3(wi,pi,rect = [0,0,max(valeurs)+10,min(max(probas)+0.2,1)],style = 2);
      xtitle(titre);
      // dessin de la fonction de repartition 
      xset('window',2);
      xbasc();
      plot2d2([0,wi],[0,cumsum(pi)],rect = [0,0,max(valeurs)+10,1.1],style = 2)
      plot2d([0,wi],[0,cumsum(pi)],rect = [0,0,max(valeurs)+10,1.1],style = -3)
      xtitle(sprintf('Fonction de repartition de la %s',titre));
    endfunction
  
    graphique_loi(titre,wi,pi);
    xclick();
  end
  
  // paramètres de la fonction cout 
  
  c=10,cm=20,cs=5;cf=200;
  
  // la fonction coût j(u,w)
  
  function y=j(u,w)
    y=c*u+cs*max(u-w,0)+cm*max(w-u,0)
  endfunction
  
  // La fonction J(u) pour la loi binomiale 
  
  function y=J(u)
    y=c*u+cs*pi*max((u-wi'),0)+cm*pi*max((wi'-u),0);
  endfunction
  
  // graphique de la fonction J(u) et recherche du minimum
  
  if %t then
    U=-10:100;
    Ju=[];
    for u=U do Ju=[Ju,J(u)];end
    xset('window',1);
    xbasc();
    plot2d(U,Ju,style = 2);
    xtitle("La fonction J");
    // recherche du minimum 
    [m,kmin]=min(Ju);
    uopt=U(kmin);
    printf("Nombre optimal de journaux a commander %f\n",U(kmin));
    printf("Moyenne de la demande %f\n",mu);
    plot2d(U(kmin),m,style = -4);// dessin
    plot2d3(U(kmin),m);
    xclick();
  end
  
  // graphique de la fonction J(u) et recherche du minimum
  // en utilisant la fonction F(z) 
  
  if %t then
    xset('window',1);
    xbasc();
    fstar=(cm-c)/(cm+cs);
    Fv=cumsum(pi);
    plot2d2([0,wi],[0,Fv],rect = [0,0,max(wi)+10,1.1],style = 2);
    plot2d([0,wi],fstar*ones([0,wi]),rect = [0,0,max(wi)+10,1.1],style = 1);
    for k=1:size(Fv,'*') do
      if Fv(k) >= fstar then kopt=k;break;end
    end
    plot2d(wi(kopt),Fv(kopt),rect = [0,0,max(wi)+10,1.1],style = -4);
    xclick()
  end
  
  // graphique de la loi du cout en fonction du paramètre u 
  
  if %t then
    function graphique_loi_cout(u,wi,pi)
      xbasc();
      xset('window',1);
      // valeurs possible des couts 
      ji1=c*u+cs*max((u-wi),0)+cm*max((wi-u),0);
      ji=unique(ji1);
      pji=0*ji;
      for i=1:size(ji,'*') do
        I=find(ji1==ji(i));
        pji(i)=sum(pi(I));
      end
      moy=pji*ji';
      vmax=min(max(pji+0.2),1);
      xmax=2000;
      plot2d3(ji,pji,rect = [0,0,xmax,vmax],style = 2);
      plot2d3(moy,vmax,rect = [0,0,xmax,vmax],style = 1);
      xtitle(sprintf('Loi de la fonction cout pour u=%f',u))
    endfunction
  
    // graphique de la loi du cout pour diverses valeurs de u 
    xset('window',1);
    xbasc();
    for u=[0:10:100] do
      graphique_loi_cout(u,wi,pi);
      xclick();
    end
  end
  
  // graphique de la loi du cout suivant le paramètre u 
  // On dessine la loi empirique obtenue avec des tirages 
  // montecarlo de la demande. 
  
  if %t then
    function graphique_loi_cout_mc(u)
      xbasc();
      xset('window',1);
      // valeurs possible des couts 
      Jv=c*u+cs*max((u-W),0)+cm*max((W-u),0);
      ji=unique(Jv);
      pji=0*ji;
      for i=1:size(ji,'*') do
        I=find(Jv==ji(i));
        pji(i)=size(I,'*')/size(Jv,'*');
      end
      moy=mean(Jv);
      vmax=min(max(pji+0.2),1);
      xmax=2000;
      plot2d3(ji,pji,rect = [0,0,xmax,vmax],style = 2);
      plot2d3(moy,vmax,rect = [0,0,xmax,vmax],style = 1);
      xtitle(sprintf('Loi de la fonction cout pour u=%f',u))
    endfunction
  
    // graphique de la loi du cout pour diverses valeurs 
    // de u 
    for u=[0:10:100] do
      graphique_loi_cout_mc(u);
      xclick();
    end
  end
  
  // On regarde ce problème comme un problème linéaire 
  // on introduit de nouvelles variables z et w pour linéariser les deux max 
  // cout = c*u + sum_s cs*pi_s* z_s +cm*y_s*w_s 
  // q in[10,100]
  // z_s >= q - x_s 
  // w_s >= x_s -q 
  
  // var=[q;z;w] 
  // Contraintes inégalité 
  
  function [A,B,C,lb,ub]=linprog_vendeur(wi,pi)
    m=size(pi,'*');
    // A*var <= B
    A=[ones(m,1),-eye(m,m),zeros(m,m);-ones(m,1),zeros(m,m),-eye(m,m)];
    B=[wi(:);-wi(:)];
    // le cout
    C=[c;cs*pi(:);cm*pi(:)];
    // bornes min et max 
    lb=[0;zeros(m,1);zeros(m,1)];
    ub=[100;%inf*ones(m,1);%inf*ones(m,1)];
  endfunction
  
  if %t then
    [A,B,C,lb,ub]=linprog_vendeur();
    [varopt,lagr,fopt]=linpro(C,A,B,lb,ub);
    usharp=varopt(1);
  end
  
  // On regarde maintenant un cas ou le vendeur à déjà des journaux 
  // et ou il paye un coup fixe si il commande des journaux 
  // on voit une stratégie [s,S] 
  
  function y=Jtilde(u,x)
    y=cf*(u > 0)+J(u+x)-c*x
  endfunction
  
  xuopt=[];
  xv=0:1:2*max(wi);
  for x0=xv do
    U=0:2*max(wi);
    Ju=[];for u=U do Ju=[Ju,Jtilde(u,x0)];end
    g=[];
    [m,kmin]=min(Ju);
    xuopt=[xuopt,U(kmin)];
  end
  
  I=find(xuopt==0);
  s=xv(I(1)-1);
  
  // vérifier que la stratégie optimale est [s,S];
  
  xset('window',1);
  xbasc();
  plot2d2(xv,xuopt,style = 2);
  plot2d2(xv(1:s),xv(1:s)+xuopt(1:s),style = 1);
  xtitle(sprintf("Valeur de s=%d et de S=%d",xv(s),xv(s-1)+xuopt(s-1)));
  
  // trouver s, S=uopt (calculé avant)
  x=0:2*max(wi);
  Jv=[];
  for i=1:size(xv,'*') do Jv=[Jv,J(x(i))];end
  costs=Jv-(cf+J(uopt));
  I=find(costs <= 0);
  if isempty(I) then
    s=0;
  else
    s=x(I(1)-1)
  end