Table des matières
Le fichier source en Scilab correspondant à ce document est accessible scilab_controle.sci.
Il est partiellement mais pas totalement corrigé. Le correction complète sera accessible
scilab_controle_corrige.sci à la fin du TP.
Vendeur de journaux : le cas de deux indices de temps
On commence par définir les caractéristiques d’une loi discrète par le vecteur (wi, 1 ≤ i ≤ N)
des valeurs possibles et la probabilité (pi, 1 ≤ i ≤ N) de chaque valeur.
w_i=[30,50,80]; p_i=[1/2,1/4,1/4]; mu=p_i*w_i';
On tire un échantillon de taille N selon cette loi. Pour la simulation on utilise grand pour
simuler une chaine de Markov dont toutes les lignes sont égales à (pi, 1 ≤ i ≤ N).
Ce qui fait le travail (exercice sur ... les chaînes de Markov), même si c’est un peu
“tordu”.
c=10,cm=20,cs=5;cf=200; function y=J(u)
y=c*u+cs*p_i*max((u-w_i'),0)+cm*p_i*max((w_i'-u),0);
endfunction
La fonction suivante calcule le minimum de J(u).
function [uopt,m]=minimum(J) U=-10:100;
Ju=[];for u=U do Ju=[Ju,J(u)];end
[m,kmin]=min(Ju); uopt=U(kmin); endfunction
Pour tracer la fonction J(u) et matérialiser le minimum remplacer %f par %t dans ce qui
suit.
if %f then xset('window',1);xbasc(); U=-10:100;
Ju=[];for u=U do Ju=[Ju,J(u)];end plot2d(U,Ju,style = 2); xtitle("La fonction J");
[uopt,m]=minimum(J); printf("Nombre optimal de journaux a commander %f\n",uopt);
printf("Moyenne de la demande %f\n",mu);
plot2d(uopt,m,style = -4); plot2d3(uopt,m);
end
On regarde maintenant un cas où le vendeur a déjà des journaux et où il paye un coup fixe
cF s’il commande des journaux. On s’attend, en optimisant, à obtenir une une stratégie de type
[s,S]. On peut le vérifier. On introduit la function 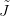 .
.
function y=Jtilde(u,x) y=cf*(u > 0)+J(u+x)-c*x endfunction
On calcule, pour x (entier) variant de 0 à 2 max(wi), la commande optimale de journaux
correspondant à chaque valeur de x.
xv=0:1:2*max(w_i);
U=0:2*max(w_i); xuopt=[]; for x0=xv do
Ju=[];for u=U do Ju=[Ju,Jtilde(u,x0)];end [m,kmin]=min(Ju); xuopt=[xuopt,U(kmin)]; end
On veut calculer s où s est la valeur maximum à partir de laquelle on passe une commande
> 0. xuopt=0 signifie que l’on commande rien pour le x correspondant. On va chercher toutes
les indices correspondant à des valeurs pour lesquelles xuopt=0.
Puis on selectionne la plus petite des valeurs d’indice i.e. I(1), la valeur de x correspondant
à l’indice juste avant (I(1)-1) va nous donner s par s=xv(I(1)-1) ;
On peut alors vérifier que la stratégie optimale est bien de la forme [s,S].
xset('window',1); xbasc(); plot2d2(xv,xuopt,style = 2);
plot2d2(xv(1:s),xv(1:s)+xuopt(1:s),style = 1);
xtitle(sprintf("Valeur de s=%d et de S=%d",xv(s),xv(s-1)+xuopt(s-1)));
[S,JS]=minimum(J); x=0:2*max(w_i);
Jv=[];for i=1:size(xv,'*') do Jv=[Jv,J(x(i))];end I=find(Jv <= cf+JS);
if isempty(I) then s=0;else s=x(I(1)-1);end; printf("On trouve s=%d et S=%d\n",s,S);
and(I(2:$)==(I(1:$-1)+1))
Vendeur de journaux : le cas de T pas de temps
On commence par décrire le système dynamique contrôlé en se restreignant à un ensemble
borné.
XMIN=-100;XMAX=100; function y=f(x,u,w) y=min(max(x+u-w,XMIN),XMAX) endfunction
La fonction de coût.
alpha=1.0; function y=ct(u,x)
y=cf*(u > 0)+c*u+alpha*cs*max(x,0)+alpha*cm*max(-x,0) endfunction function y=c0(u)
y=cf*(u > 0)+c*u endfunction function y=K(x)
y=cs*max(x,0)+cm*max(-x,0)
endfunction function res=cout(t,x,u)
if t==1 then res=c0(u); else
res=ct(u,x); end endfunction function cost=ecost(t,x,u,cout,Vtp1)
cost=0; for l=1:size(w_i,'*') do
xtp1=f(x,u,w_i(l));
ix=find(xtp1==ensemble_etats);
cost=cost+p_i(l)*Vtp1(ix); end; cost=cout(t,x,u)+cost;
cost=alpha^t*cost; endfunction
On calcule v(t,x) à l’aide de l’équation de Bellman. On commencera avec T = 2 : 2 indices
de temps (0 et 1) qui correspond le problème à un pas de temps.
T=2; ensemble_etats=XMIN:XMAX;
ensemble_controles=0:XMAX;
On commence par diverses initialisations. On affecte αT × K(.) à v(T,.). On va calculer
V (t,.) pour T − 1,..., 1 et stocker les résultats du calcul de V (t,.) dans une liste L et de la
commande (feedback) optimale U(t,.) dans U.
VT=alpha^T*K(ensemble_etats);
L=list(VT);
U=list(0);
On exécute la boucle rétrograde en temps pour résoudre l’équation de Bellman.
for t=T-1:-1:1 do printf("t=%d\n",t);
Vt=zeros(1,size(ensemble_etats,'*')); Ut=%nan*ones(1,size(ensemble_etats,'*'));
Vtp1=L($);
for i=1:size(ensemble_etats,'*') do
x=ensemble_etats(i); mcost=%inf;
for k=1:size(ensemble_controles,'*') do u=ensemble_controles(k);
cost=ecost(t,x,u,cout,Vtp1);
if cost < mcost then mcost=cost; kumin=k; end end
Vt(i)=mcost;
Ut(i)=ensemble_controles(kumin); end
L($+1)=Vt; U($+1)=Ut; end
Dessin de la fonction de Bellman et de la commande optimale au temps t = 1.
xset('window',1); xbasc(); plot2d2(ensemble_etats,L($));
xset('window',1); xbasc(); plot2d2(ensemble_etats,U($));
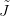 .
.
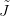 .
.