Contents

L’objet de ce TD est de simuler numériquement la dissipation de la pression interstitielle et le tassement dans une couche de matériau poroélastique soumise à une surcharge de type échelon. On réalisera un script Scilab fournissant une solution approchée du problème poromécanique couplé. L’approximation spatiale sera réalisée avec une interpolation quadratique en déplacement et linéaire en pression et l’approximation temporelle par un schéma implicite en pression.

Problématique

On se propose de déterminer numériquement la solution du problème dit “de la consolidation” d’une couche de matériau poroélastique soumise à une surcharge constante.

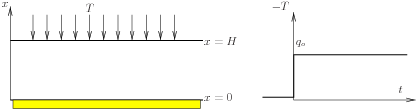
La structure considérée est délimitée par les plans x = 0 et x = H. Son extension dans les directions horizontales y et z est infinie. La face inférieure est en contact avec un socle fixe et imperméable. La face supérieure est drainée (pression maintenue à 0). Elle est soumise à une distribution surfacique uniforme de forces verticales T = Te_x dont la variation dans le temps est de type échelon :

Compte tenu de la géométrie du problème, la seule variable d’espace est la coordonnée verticale x et le déplacement est colinéaire à e_x, c’est-à-dire de la forme ξ = ξ(x,t)e_x. Les inconnues du problème sont la pression p(x,t) et la fonction ξ(x,t).

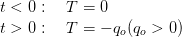
On adopte une discrétisation par éléments finis en espace et par le schéma d’Euler implicite en temps. On suppose connus le déplacement et la pression au temps t et on cherche ces grandeurs à l’instant t + δt où δt est le pas de temps. On note δp et δξ la différence entre la pression et le déplacement, respectivement, entre les instants t et t + δt. Compte tenu des hypothèses mécaniques introduites ci-dessus, les fonctions δp et δξ sont régies par les équations suivantes

où λ₀, μ₀, b, M et k sont des paramètres.

L’état avant application de l’échelon étant naturel, on admet que la réponse à l’échelon à l’instant t = 0⁺ est une distribution uniforme de pression dans la couche, égale à

où λ_nd et μ_nd désigne les caractéristiques dites non drainées du matériau. Dans la suite, l’intervalle d’étude est [0⁺, +∞]. En particulier, la configuration à l’instant t = 0⁺ est prise comme référence pour le calcul des déplacements. La pression initiale est donc uniforme, égale à p_o. On s’intéresse à la dissipation progressive de la pression p(x,t) ainsi qu’au tassement ξ(H,t) associé à cette dissipation.

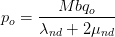
On adopte un maillage uniforme du segment [0,H] en n mailles [x_i,x_i+1]. L’interpolation est linéaire pour la pression, et quadratique pour le déplacement. On note (φ_i^p) _1≤i≤n+1 les fonctions de forme pour la pression et (φ_i^ξ) _1≤i≤2n+1 les fonctions de forme pour le déplacement. On introduit les matrices [K], [N] et [B] de terme générique

Pour les applications numériques, on prendra les caractéristiques poroélastiques λ_o + 2μ_o et M égales à l’unité, fixant ainsi l’échelle des pressions. La solution étant manifestement linéaire en p_o, on fixera également p_o à l’unité. Le coefficient de Biot (adimensionnel) b sera pris égal à 1. L’évolution des pressions étant contrôlée par le temps adimensionnel T = ct∕H², il sera commode de prendre H = 1m. On décomposera la couche en n = 10 éléments finis. Notant dx l’épaisseur des éléments finis, on choisira le pas de temps dt de façon à ce que cdt∕dx² = 0.1.

Rappel sur l’animation graphique

Pour réaliser une animation, il convient d’initialiser la fenêtre graphique avant la boucle en temps de la façon suivante :

La commande driver("X11") permet d’accélérer l’affichage en ne stockant pas en mémoire toutes les données relatives au tracé de la courbe mais seulement les plus importantes (perte de la possibilité du zoom par exemple). La commande xset("pixmap",1) évitera le clignotement de la fenêtre lors de la boucle en temps. Au sein de la boucle en temps, la fenêtre graphique est rafraichie de la façon suivante :

La commande xset("wwpc") efface le contenu courant de la fenêtre graphique en mémoire. La commande xset("wshow") affiche dans la fenêtre graphique le contenu courant de la mémoire.