Déplétion d’un réservoir pétrolier

Luc Dormieux et Alexandre Ern
(last modification date: April 9, 2018)
Version pdf de ce document
Version sans bandeaux

1 problématique
2 Discrétisation en temps
3 Discrétisation en espace
4 Formulation du schéma numérique
5 Implémentation sous Scilab
6 Simulations numériques
7 Amélioration des performances numériques

Contents

1 problématique
2 Discrétisation en temps
3 Discrétisation en espace
4 Formulation du schéma numérique
5 Implémentation sous Scilab
6 Simulations numériques
7 Amélioration des performances numériques
 7.1 Préfactorisation des inverses matricielles
 7.2 Mise à profit des structures creuses des matrices

L’objet de ce TD est de simuler numériquement la dépletion d’un réservoir pétrolier. On se placera dans le cadre de l’hypothèse œdométrique ce qui permettra de modéliser les variations spatiales et temporelles du champ de pression dans le réservoir par une équation de la chaleur. De plus, on se placera en configuration axisymétrique. On réalisera un script Scilab fournissant une solution approchée de l’équation de la chaleur unidimensionnelle en coordonnées radiales. L’approximation spatiale sera réalisée avec un élément fini P1 conforme et l’approximation temporelle par le schéma d’Euler explicite ou implicite.

1 problématique

Un réservoir pétrolier est une formation rocheuse perméable dont l’espace poreux est partiellement saturé par des hydrocarbures. Au terme d’un mouvement ascendant depuis la zone de formation des hydrocarbures, appelée roche mère, ceux-ci viennent se piéger dans le réservoir en raison de l’imperméabilité des couches limitant supérieurement ce dernier. L’accumulation progressive d’hydrocarbures conduit à l’existence d’une pression dans le réservoir. On s’intéresse dans ce TD à la séquence de production primaire qui consiste à réaliser un puits dans le réservoir et à tirer parti de la pression initiale qui y règne pour récupérer les hydrocarbures. Il suffit pour cela que la pression de puits pp soit plus basse que la pression de réservoir.
Pour simplifier, on suppose que le réservoir est un cylindre horizontal plat ℛ de rayon L entouré de formations imperméables. L’ordre de grandeur du rayon de puits rp est décimétrique, tandis que celui de L est de l’ordre de plusieurs centaines de mètres. On suppose que les hydrocarbures saturent totalement l’espace poreux et que la pression initiale d’hydrocarbure est uniforme. Elle est notée p0. La roche constituant le réservoir est modélisée comme un matériau poroélastique linéaire (modules d’élasticité λo, μo coefficient de Biot b, perméabilité k).
Une fois le puits réalisé, on suppose que l’évolution du réservoir est régie par l’hypothèse œdométrique :

où e1 désigne la direction verticale. Dans ces conditions, la pression ne dépend que du rayon r compté à partir de l’axe du puits et du temps t.

Le réservoir étant initialement à la pression uniforme p0, on impose à partir de l’instant t = 0 une pression de puits pp nulle en r = rp ≈ 0.

Question 1 Montrer qu’avec les hypothèses envisagées, le champ de pression p(r,t) dans le réservoir est solution de

(| ∂tp − c1∂r(r∂rp) = 0 (r,t) ∈ ]0,L [ × ]0,+ ∞ [ ||{ r p(0,t) = 0 t ∈ ]0,+∞ [ || ∂rp(L, t) = 0 t ∈ ]0,+∞ [ |( p(r,0) = p0 r ∈ ]0,L [
(1)

avec

( b2 1 ) −1 c = k ---------+ --- . λo + 2μo M

On se propose de quantifier la séquence de production primaire à l’aide de l’indice de récupération I(t) défini comme la quantité d’hydrocarbures (supposés ici incompressibles) produite entre l’instant où débute la production et l’instant t, rapportée à la quantité d’hydrocarbures initialement présente dans le réservoir. On a donc

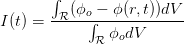
∫ -ℛ(ϕo-−-ϕ-(r,-t))dV-- I(t) = ∫ ϕ dV ℛ o
où ϕ(r,t) et ϕo désignent respectivement les porosités lagrangiennes actuelle et initiale.

Question 2 Montrer que l’indice de récupération asymptotique est

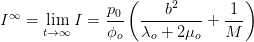
( ) ∞ p0 b2 1 I = lti→m∞ I = --- ---------+ --- ϕo λo + 2μo M
On pose alors Q(t) = I(t)∕I∞. Montrer que
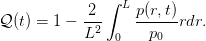
∫ -2- L p(r,t) 𝒬(t) = 1 − L2 p rdr. 0 0

2 Discrétisation en temps

On se donne un pas de temps δt et on pose tn = nδt pour n entier positif. La dérivée temporelle ∂tp dans (1) est discrétisée à l’aide de différences finies en temps. En notant pn(r) l’approximation du champ de pression à l’instant discret tn, on aboutit au problème suivant : étant donné pn, trouver pn+1 solution de

( || pn+1 − pn − cδt1r∂r(r∂rpn+ α) = 0 r ∈ ]0, L[ |{ n+1 p (0) = 0 || ∂rpn+1(L ) = 0 |(
(2)

avec la condition initiale p0 = p 0. Ici, α vaut 0 pour le schéma d’Euler explicite et 1 pour le schéma d’Euler implicite.

3 Discrétisation en espace

On discrétise maintenant (2) en espace. On se donne un maillage non-uniforme de l’intervalle [0,L] sous la forme

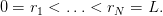
0 = r1 < ... < rN = L.
Pour 1 ≤ i ≤ N − 1, on note hi = ri+1 − ri et pour 1 ≤ i ≤ N, on note φi la fonction chapeau associée au nœud ri. On choisit de prendre en compte la condition de Dirichlet en r = 0 par une méthode de pénalisation : pn+1 est donné par la formulation variationnelle
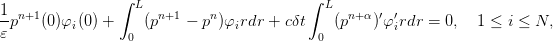∫ ∫ 1 n+1 L n+1 n L n+ α ′ ′ -p (0)φi(0) + (p − p )φirdr + cδt (p )φ irdr = 0, 1 ≤ i ≤ N, 𝜀 0 0
(3)

où 𝜀 est le paramètre pour la pénalisation de la condition de Dirichlet. Par la suite, on prendra 𝜀 = 10−12.

4 Formulation du schéma numérique

En notant Pn le vecteur dont les composantes sont les pn(r i), 1 ≤ i ≤ N, montrer que (3) s’écrit sous la forme matricielle

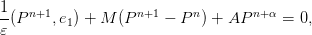1- n+1 n+1 n n+α 𝜀 (P ,e1) + M (P − P ) + AP = 0,
(4)

où e1 = (1, 0,…, 0) et où M et A sont des matrices d’ordre N dont on précisera les coefficients.

Question 3 Montrer que le schéma numérique s’écrit sous la forme matricielle

ZlPn+1 = ZrP n,
(5)

où Zl et Zr sont des matrices d’ordre N qu’on évaluera en fonction de M, A et 𝜀 pour les schémas explicite et implicite.

Question 4 Evaluer 𝒬n = 𝒬(tn) de façon analytique en fonction des coordonnées du vecteur Pn.

5 Implémentation sous Scilab

Question 5 Ecrire un script Scilab mettant en œuvre le schéma (5).

On s’inspirera des conseils ci-dessous et de l’aide en ligne.

  1. terminer toutes les lignes de commande par un point virgule ; (sauf celles pour lesquelles on souhaite afficher dans la fenêtre scilab le résultat numérique de la commande).
  2. une ligne de commentaires doit commencer par //.
  3. initialiser le script par la commande clear all; qui nettoye l’espace mémoire occupé.
  4. initialisation du maillage : utiliser une fonction
      function [u] = shapex(t)
        a = ...;
        u = atanh(tanh(a)*t) / a;
      endfunction
      x = L * shapex(linspace(0,1,nx));

    Le paramétre a contrôle la finesse des mailles près de r = 0.

    Question 6 Pour quelle valeur de a construit-on un maillage uniforme ? Quel est l’effet d’une augmentation de la valeur de a ?

  5. on introduira une variable qu’on pourra appeler euler, qui prendra les valeurs 1 et 2 et qui codera pour le schéma explicite ou implicite. La syntaxe est la suivante
      euler = ...; // 1=explicite, 2=implicite
      select euler
       case 1
        ...; // commandes pour le cas explicite
       case 2
        ...; // commandes pour le cas implicite
      end
  6. programmation d’une boucle : par exemple
      for i = 1:nx
        ...
      end
  7. mise en œuvre du schéma (5) :
      unew = inv(ZL) * ZR * u;
  8. animation graphique : avant la boucle en temps, il convient pour réaliser une animation d’initialiser la fenêtre graphique de la façon suivante :
      driver("X11")
      xselect()
      xbasc()
      xset("pixmap",1)

    La commande driver("X11") permet d’accélérer l’affichage en ne stockant pas en mémoire toutes les données relatives au tracé de la courbe mais seulement les plus importantes (perte de la possibilité du zoom par exemple). La commande xset("pixmap",1) évitera le clignotement de la fenêtre lors de la boucle en temps. Au sein de la boucle en temps, la fenêtre graphique est rafraichie de la façon suivante :

        xset("wwpc")
        plot2d(temps(1,1:l+1),qqq(1,1:l+1),rect=[0,0,Tmax,1]);
        xset("wshow")

    La commande xset("wwpc") efface le contenu courant de la fenêtre graphique en mémoire. La commande xset("wshow") affiche dans la fenêtre graphique le contenu courant de la mémoire. l est l’indice courant de la boucle en temps, temps est le vecteur contenant les valeurs des instants discrets tm pour 0 ≤ m ≤ l et qqq(m) vaut 𝒬m.

  9. afin de mesurer le temps d’exécution du script, on insérera la commande
      timer();

    avant le démarrage de la boucle en temps et la commande

      timer()

    à la fin de celle-ci. Le temps d’exécution écoulé entre les 2 appels de la fonction timer sera affiché dans la fenêtre Scilab.

  10. on affichera également le temps tm au bout duquel l’indice de récupération atteint 90% de sa valeur asymptotique.

6 Simulations numériques

Question 7 Montrer que la dépendance en temps de la pression et de l’indice de récupération est contrôlée par un temps adimensionnel.

Evaluer l’échelle de temps pour les valeurs numériques suivantes (appropriées pour un réservoir de grès) : viscosité du fluide 10−3 Pa⋅s, perméabilité intrinsèque 10−14 m2, λ o = 1.5 GPa, μo = 0.75 GPa, M = 50 GPa, b = 0.9 et L est de l’ordre de 100 à 500m.

Notre objectif est de réaliser des simulations numériques afin de déterminer la valeur du temps adimensionnel pour laquelle on atteint 90% de l’huile susceptible d’être produite. On notera t90% ce temps. Pour les simulations numériques, on prendra L = 1 et c = 1, la dimensionnalisation de t90% se faisant via l’échelle de temps calculée ci-dessus.

Considérer d’abord un maillage uniforme avec N = 10 et un temps de simulation de T = 10.

Question 8 Vérifier que le schéma explicite n’est stable que si le pas de temps est suffisamment petit. Estimer numériquement le seuil de stabilité. Qu’en est-il pour le schéma implicite ? Commenter l’efficacité relative des deux schémas.

Par la suite, on ne considérera que le schéma implicite.

Question 9 Faire un premier calcul de t90% sur maillage uniforme (N = 10) et avec δt = 0.1. Comparer par rapport à la valeur obtenue avec un calcul très précis (N = 1000 et δt = 0.01) qui est de t90% ≃ 9.7. Etudier les améliorations obtenues en augmentant N et en travaillant sur maillage non-uniforme (on pourra par exemple réaliser une simulation avec N = 100 et a = 1 puis a = 4). Quelle est approximativement la valeur maximale de N que l’on peut considérer sans saturer complètement l’espace mémoire Scilab ? Commenter par rapport à l’estimation de t90%.

7 Amélioration des performances numériques

Deux pistes seront explorées.

7.1 Préfactorisation des inverses matricielles

On pose

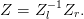
Z = Z−l1Zr.

Question 10 Expliquer pourquoi il est intéressant de précalculer la matrice Z avant de lancer la boucle en temps. Faire quelques essais numériques afin de quantifier les gains en temps de calcul.

7.2 Mise à profit des structures creuses des matrices

L’assemblage d’une matrice A tenant compte de sa structure creuse (ici tridiagonale) se fait de la manière suivante

  ij = [;];
  v  = [];
  for i = 1:nx-1
    ij = [ij; i,i]; v = [v, \alpha_{i,i}];
    ij = [ij; i+1,i]; v = [v, \alpha_{i+1,i}];
    ij = [ij; i,i+1]; v = [v, \alpha_{i,i+1}];
    ij = [ij; i+1,i+1]; v = [v, \alpha_{i+1,i+1}];
  end

où αij est la contribution de la maille [ri,ri+1] au terme d’indice (i,j) dans la matrice A. Le résultat de cette opération sont deux vecteurs, ij qui contient la liste de tous les couples d’indices (i,j) pour lesquels le coefficient Aij est non nul et v qui contient les valeurs correspondantes de Aij. Noter que si un couple (i,j) apparaît deux fois dans ij, les valeurs correspondantes dans v seront cumulées.

L’assemblage de la matrice A se fait simplement en utilisant la commande

  A = sparse(ij,v);

L’inversion d’une matrice creuse se fait en deux étapes :

Question 11 Créer un nouveau script Scilab utilisant les fonctions décrites ci-dessus. Comparer les performances numériques par rapport à l’approche ne tirant pas profit des structures creuses, notamment dans le cas de maillages fins en espace.