Contents
L’objectif de ce TP en scilab est d’illustrer numériquement les techniques d’accélération de
convergence vues en cours. On se place dans le modèle à volatilité stochastique suivant
:
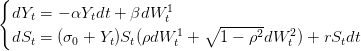 | (1) |
où α,β > 0, Y 0 = 0, ρ ∈ [−1, 1] et (W1,W2) est un mouvement brownien de dimension
2.
Pour une option européenne d’échéance T et de payoff f(St,t ≤ T) on souhaite calculer
𝔼(e−rT f(S
t,t ≤ T)). Bien entendu, il est nécessaire pour cela de discrétiser l’équation différentielle
stochastique (1) : on note N ∈ ℕ∗ le nombre de pas de temps, Δt = T∕N le pas de discrétisation et
pour k ∈{0,…,N}, tk = kΔt le k-ème instant de discrétisation.
Nous allons successivement étudier
- dans le cas d’un Call vanille (f(st,t ≤ T) = (sT −K)+) les techniques de réduction de
variance qui à N fixé permettent de réduire le nombre de trajectoires indépendantes
nécessaires pour obtenir une erreur statistique donnée.
- dans le cas d’un Call barrière Up and Out (f(st,t ≤ T) = 1{max [0,T]st<b}(sT −K)+) les
techniques de pont brownien qui permettent d’accélerer la décroissance du biais avec
N.
1 Réduction de variance
On note Xt = e−rtS
t le sous-jacent actualisé.
- Calculer dXt puis écrire le payoff actualisé du Call vanille à l’aide de XT .
- Quelle est la loi du couple (Y tk+1 − e−αΔtY
tk,Wtk+11 − W
tk1)? Et celle du vecteur
(Y tk+1 − e−αΔtY
tk,ρ(Wtk+11 − W
tk1) +
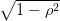 (W
tk+12 − W
tk2))?
(W
tk+12 − W
tk2))?
- Quel est l’intérêt du schéma de discrétisation suivant
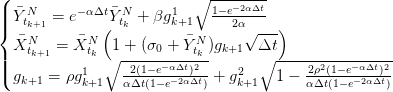 | (2) |
où (gk1,g
k2)
k≥1 est une suite de couples i.i.d. avec g11 et g
12 gaussiennes centrées réduites
indépendantes? C’est ce schéma que nous allons utiliser dans la suite.
1.1 Conditionnement
On se place dans le cas ρ = 0 où le mouvement brownien qui dirige le processus Y et le mouvement
brownien qui dirige le processus X sont indépendants.
- Comment le schéma se simplifie-t-il? Implémentez-le sous forme vectorielle dans le
programme VScondit_Q.sce en prenant garde à mettre à jour X avant de mettre à
jour Y .
- Que vaut Z = 𝔼((XT − Ke−rT )+|Y
t,t ≤ T)? Comment comparer V ar(Z) et
V ar((XT − Ke−rT )+)?
- Stockez dans la variable somcarsig la somme des carrés des volatilités utilisées sur
chaque pas de temps. Que représente
 ?
?
- Exécuter le programme (exec VScondit_Q.sce). Quelle réduction de variance
obtient-on par conditionnement? Comment évolue le facteur de réduction avec le
niveau moyen de la volatilité σ0? Et avec le niveau β du bruit de la volatilité? Est-ce
intuitif?
1.2 Variable de contrôle construite avec le modèle de Black-Scholes
On ne suppose plus ρ = 0 et on va utiliser (S0eσ0(ρWT1+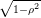 WT2)−
WT2)−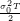 −Ke−rT )+ comme variable
de contrôle pour le calcul du prix du Call.
−Ke−rT )+ comme variable
de contrôle pour le calcul du prix du Call.
- Implémentez le schéma général dans le programme VSvarcontBS_Q.sce. Implémentez
également l’évolution du processus de Black-Scholes actualisé pour la volatilité σ0 avec
les mêmes accroissements browniens que ceux qui dirigent X.
- Stockez dans le vecteur paycont les payoffs correspondant au sous-jacent actualisé moins
ceux correspondant au processus de Black-Scholes actualisé. Exécutez le programme
(exec VSvarcontBS_Q.sce).
1.3 Régression sur le sous-jacent actualisé
- Que vaut 𝔼(XT N)? Pour quelle valeur γ∗ de γ la variance de (X
T N−Ke−rT )+−γX
T N
est-elle minimale? Estimez γ∗ dans la variable coef du programme VSvarcontS_Q.sce
puis exécutez ce programme.
- L’évolution du facteur de réduction de variance avec le strike K est-elle conforme à
l’intuition?
2 Réduction du biais pour les options barrières
On s’intéresse au Call Up and Out de payoff 1{max [0,T]St<b}(ST − K)+.
- Déduire de (2) un schéma (StkN,Y
tkN)
0≤k≤N permettant de simuler le sous-jacent S.
- Que vaut ℙ
![( )
max S¯N ≥ b|Y¯N , ¯SN , ¯SN
[tk,tk+1] t tk tk tk+1](acceleration6x.png) ?
?
- Implémentez le schéma et mettez à jour la probabilité conditionnelle pour que
le schéma en temps continu n’ait pas franchi la barrière dans le programme
VSbarriere_Q.sce. Exécuter ce programme avec β = 0 pour comparer avec la formule
explicite qui donne le prix de l’option barrière dans le modèle de Black-Scholes avec
volatilité σ0. Reprendre avec β = 0.1.
2.1 Options asiatiques
Exécuter le fichier suivant BSasiat.sce
2.2 Réponses
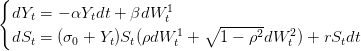
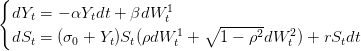
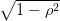 (W
tk+12 − W
tk2))?
(W
tk+12 − W
tk2))?
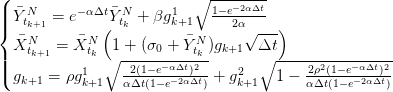
 ?
?
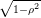 WT2)−
WT2)−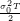 −Ke−rT )+ comme variable
de contrôle pour le calcul du prix du Call.
−Ke−rT )+ comme variable
de contrôle pour le calcul du prix du Call.
![( )
max S¯N ≥ b|Y¯N , ¯SN , ¯SN
[tk,tk+1] t tk tk tk+1](acceleration6x.png) ?
?