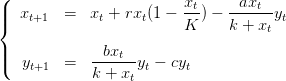
Les serres du Sud de la France subissent chaque année l’invasion de colonies de pucerons pendant les cents jours nécessaires pour obtenir le grossissement et la maturation du concombre. Les dommages causés par ces insectes peuvent se révéler particulièrement importants, entrainant parfois même, en absence de traitement, la destruction du plant. L’utilisation de la coccinelle en tant qu’agent de lutte biologique à grande échelle est une option jusqu’à lors peu utilisée par les agriculteurs et que des biologistes ont décidé d’explorer.
L’introduction de ces coccinelles se fait de façon empirique dans les exploitations. Ici, nous nous plaçons dans une optique de minimisation des coûts sous dynamique biologique et cherchons les stratégies optimales d’introduction des coccinelles. Dans un premier temps, nous étudions le couple coccinelles pucerons quand les coccinelles introduites sont stériles et dans un deuxième temps quand celles-ci ont la capacité de se reproduire.
Ici, la proie est le puceron A.gossypii. Espèce vivant sur les cucurbitacés, on le retrouve en particulier sur les plants de concombre. Sa présence est particulièrement nocive dans une culture à cause de ses capacités reproductives très rapides. Un ailé pond ses œufs sur une feuille de concombre et, au bout de 2 ou 3 jours, la colonie prend la forme d’une pièce de monnaie qui grossit peu à peu pour atteindre au bout de dix jours un recouvrement total de toute la feuille. Le puceron adulte atteint une masse de 1 mg. La colonisation par la marche peut alors commencer alors que, parallèlement, de nouveaux ailés quittent la feuille pour coloniser d’autres plants. Le puceron a en effet cette capacité d’adaptation au milieu qui lui permet, quand son environnement est saturé en congénaires, de produire des ailés pour étendre la colonie. Ainsi en une quizaine de jours, les pucerons peuvent coloniser toute la serre. Or les ravages causés aux cultures sont très importants : les pucerons sucent la sève de la plante ce qui entraîne son asphyxie. Leurs déjections sont également un poison pour la plante. C’est pourquoi, il nous faut un auxiliaire efficace de lutte biologique, car dès que le nombre de pucerons est d’environ 10 000 par plant, la qualité de celui-ci est dépréciée et la présence d’environ 100 000 d’entre eux entraîne la destruction de la plante.
Ici, le prédateur est la coccinelle H.axyridis. Les couleurs de ces coccinelles sont variées mais leurs caractéristiques physiologiques sont identiques. Elle mesure 6 millimètres de long sur 5 millimètres de large et pèse 100 mg. Ces coccinelles sont d’excellents prédateurs pour les espèces d’aphides et donc constituent un outil privilégié dans la lutte biologique contre les pucerons. C’est une espèce qui présente un dévelopement précoce au cours de l’année ainsi qu’une grande capacité reproductrice. De plus, son développement structuré en stades accroît son potentiel à consommer des pucerons. On distingue en effet quatre stades de croissance:
Le système pucerons-coccinelles que nous étudions présente un pas de temps naturel, celui de la journée.
Les variables d’état du modèle sont
et ses paramètres sont
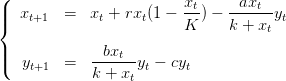 | (1) |
Question 1 Trouver les coordonnées (i,i)i∈[1;3] des points d’équilibre Pi,i∈[1;3] du système pucerons-coccinelles non commandé. Établir la matrice Jacobienne des points P1 et P2 et étudier leur stabilité.
Remarque: On montre qu’une condition suffisante de stabilité du point P3 est
K(1 −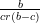 ) <
) < 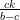 .
.
Question 2 Saisir le code suivant dans le fichier TP_Lutte_biologique_1.sce et simuler des trajectoires partant de x = 100 000 et y = 10 000, soit 100 000 pucerons et 100 coccinelles. Représenter l’évolution quantitative de la biomasse de pucerons et de coccinelle en fonction du temps. Représenter également le portait de phase .
Question 3 Application numérique: Sachant que
∙ r=0.4;
∙ a=2;
∙ K=40000;
∙ b=1;
∙ k=100000;
∙ c=0.1;
interpréter les trajectoires et le portrait de phase.
Dans ce premier modèle, nous considérons un stock de coccinelles pour lesquelles il est impossible de se reproduire. On fixe la valeur de ce stock égale à ymax. On considère donc que les seules coccinelles présentes dans le milieu sont celles que nous introduisons, c’est-à-dire que nous leur otons la faculté de se reproduire. L’équation régissant la prolifération de la population de coccinelles disparaît donc de la dynamique (1). La biomasse de pucerons obéit alors à la dynamique
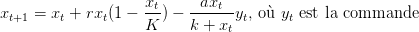 | (2) |
On note
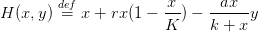 | (3) |
On considère alors le problème de minimisation des coûts
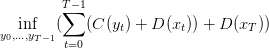 | (4) |
avec la dynamique
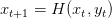 | (5) |
et sous les contraintes
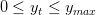 | (6) |
Ici,
Nous étudions l’évolution du système pucerons-coccinelles sur une durée de 100 jours, durée de la saison de la culture du concombre, avec une fréquence quotidienne d’introduction de coccinelles. On prendra donc T de l’ordre de 100.
Pour résoudre (4), (5), (6), nous utilisons la méthode de la programmation dynamique. L’équation de Bellman correspondant à notre problème de minimisation des coûts est
![{
V (x,T ) = D (x)
V (x,t) = min0 ≤y≤ymax[C(y ) + D (x) + V (H (x, y),t + 1)]](Lutte_biologique8x.png) | (7) |
Nous minimisons le coût d’introduction des coccinelles et les dommages causés par les pucerons de t = 0 à t = T − 1. Le coût instantané L est donc
![∀t ∈ [0,T − 1 ],L(x,y, t) = α + βy + D (x)](Lutte_biologique9x.png) | (8) |
D(x) pouvant prendre plusieurs expressions mathématiques selon le modèle que l’on désire tester.
Le coût final Φ est
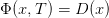 | (9) |
La résolution de l’équation (7) nous permet, à chaque pas de temps, de trouver de façon rétrograde le feedback optimal y#(x,t). y#(x,t) signifie que la biomasse optimale de coccinelles à introduire au temps t dépend de la biomasse de pucerons.
Le coût d’introduction des coccinelles au sein la colonie de pucerons est la somme de deux coûts :
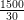 = 50 euros, salaire quotidien du technicien.
= 50 euros, salaire quotidien du technicien.L’expression du coût d’introduction est donc très simple car tous les problèmes de modélisation économique de culture, d’élevage et de conditionnement des coccinelles sont résumés dans le prix de vente unitaire d’une coccinelle.
Nous allons considérer deux types de fonction de dommages :
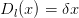 | (10) |
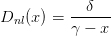 | (11) |
La dynamique utilisée est
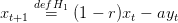 | (12) |
Vous procéderez à l’étude analytique complète d’une dynamique linéaire couplée avec une
fonction de dommages linéaire (4.4.1) et vous présenterez les premières étapes de
résolution d’une dynamique linéaire couplée à avec une fonction de dommages non linéaires
(4.4.2). Nous nous limitons à ces deux cas car la résolution analytique de probl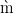 es
d’optimisation dynamique est en général difficile. Nous en verrons un exemple dans le paragrahe
(4.4.2).
es
d’optimisation dynamique est en général difficile. Nous en verrons un exemple dans le paragrahe
(4.4.2).
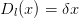 |
Question 5 Quel type de réponse classique observe-t-on? Commentez le résultat d’un point de vue économique.
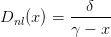 |
Question 6 Calculer la fonction valeur jusqu’à l’avant dernière décision. Observer la difficulté de poursuivre le calcul et de trouver une formulation générale de la fonction valeur de Bellman.
Face aux difficultés analytiques pour déterminer une expression de la fonction valeur de Bellman, nous utilisons des simulations numériques. Pour cela nous allons en premier lieu effectuer la discrétisation du problème.
Nous considérons une population de pucerons dont la biomasse varie de 0 à 100 000 pucerons. Chaque puceron pesant 1 mg, la population étudiée génère alors jusqu’à 100 000 états possibles pour les pucerons. Or, il est évidemment très coûteux en temps lors de la simulation de créer un nombre aussi élevé d’états. C’est pourquoi nous nous limitons à p = 500 états possibles pour la biomasse de pucerons, états pris dans l’ensemble {0,h, 2h,..., 5 000h} où h représente la biomasse de 200 pucerons.
De la même façon, la quantité de coccinelles introduites étant nécessairement un multiple de la biomasse d’une coccinelle, nous utilisons un échantillonage variant de 0 à 10 000 mg de coccinelles introduites dans le milieu avec un pas entre chaque valeur de la commande y de 100 mg, valeur de la biomasse d’une coccinelle. Cela représente donc une introduction de 0 à 100 coccinelles.
La discrétisation du problème (2) conduit à discrétiser la dynamique. Pour cela, nous utilisons des matrices de transition qui vont pour chaque biomasse de puceron dans le milieu nous donner la discrétisation de la biomasse image de la biomasse initiale par la dynamique H. Donc, à chaque image correspond deux biomasses discrétisées Xi et Xi+1, telles que Xi < X < Xi+1. Ces matrices nous permettent d’associer à chaque biomasse de puceron prise entre 0 et 100 000 mg, la biomasse de pucerons discrétisée appartenant à la grille {0,h, 2h,..., 5 000h} définie en 4.5. La dynamique H permet de calculer l’image X de la biomasse x considérée initialement. X appartient alors à l’intervalle [Xi,Xi+1] formé par deux éléments de la grille.
À Xi et Xi+1 sont associées des probabilités d’atteignabilité. Ainsi, pour chaque valeur de la commande y,
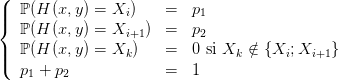 | (13) |
Alors, pour chaque valeur de la commande est créée une matrice de transition My(x,y), indicée par la commande y et telle que Mijy = ℙ(H(x i,y) = xj). Cette matrice est très creuse et permet le stockage des états possibles de la biomasse de pucerons. Nous avons ainsi discrétisé la dynamique du problème ( 2)
Le coût instantané est une liste de cardinal le nombre de commandes applicables au système (2), de taille (cardinal_etat,horizon), cardinal_etat étant le cardinal de l’espace d’état pucerons. Nous rappelons que le coût instantané L, pour t ∈ [0,T − 1] et le coût final Φ sont
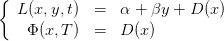 | (14) |
Question 7 Recopier les paramètres suivant dans un fichier parametres.sce
Question 8 Recopier le code suivant dans un fichier fonctions.sci . Il donne le résultat de la dynamique commandée à chaque couple pucerons-coccinelles, ainsi que les fonctions de dommages et de coût final.
Question 9 Recopier le code suivant dans un fichier macro_discretisation.sci
Puis on crée la matrice faisant correspondre pour chaque état l’image discrétisée inférieure xj, (respectivement supérieure xj+1) ainsi que le vecteur des probabilités associées, indices_image_discretisee(3) pour xj, (respectivement 1-indices_image_discretisee(3) pour xj+1, le code correspondant étant
On poursuit par remplissage de deux sous-matrices de transition, en utilisant la fonction sparse
La matrice de transition terminale est donc la somme des deux sous-matrices de transition.
Question 10 Créer un fichier TP_Lutte_biologique_2.sce dans lequel vous recopiez le code suivant.
Question 11 Exécuter le fichier Lutte_biologique_2.sce. Vérifier que la liste de matrices matrice_transition est bien formé de sparses matrices de transition, c’est à dire de matrices formées de trois colonnes dont la somme des coefficients positifs ou nuls de la dernière colonne, relatifs au même élément de la première colonne, est égale à 1.
Recopier dans un fichier prog_dyn.sci les codes suivant:
Explicitons le problème de la discrétisatio de l’EDP (interpolation linéaire)
Voici l’étape de programmation qui permet le calcul rétrograde des fonctions valeurs de Bellman et des feedbacks optimaux. À chaque pas de temps et pour chaque valeur du vecteur commande, on effectue le calcul de
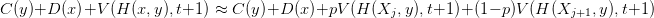 | (15) |
grâce à
Puis on prend le minimum des valeurs à chaque pas de temps, ainsi que l’indice de la commande qui donne le feedback optimal.
Ces valeurs sont réinjectées à chaque pas de temps dans la récurrence.
Question 12 Recopier, à la suite du code déjà inscrit le code suivant dans le fichier TP_Lutte_biologique_2.sce.
Nous avons désormais construit toute l’architecture du code nécessaire pour effectuer les simulations.
Nous allons tester les réactions du programme sur plusieurs cas particuliers. Toutes les valeurs
numériques ont été choisies pour que les dommages causés par 2 000 pucerons soient égaux aux
coûts d’introduction de la quantité maximale de coccinelles. Les dynamiques utilisées pour simuler
les cas particuliers étudiés dans la partie théorique nous conduisent à adapter la valeur du
paramètre a. Nous effectuons une mise à l’échelle pour éviter une discrétisation abusive
du vecteur image qui prendrait pour la plupart des commandes la valeur 0 à cause
de la discrétisation, faussant ainsi les résultats des simulations : cet ajustement est
indispensable car des situations aussi particulières que des réponses en “bang-bang” peuvent
présenter des marches intermédiaires théoriquement fausses. Les valeurs des paramètres
sont
∙ δ = 0.302
∙ a = 10−6
∙ r = 2.10−2
∙état initial= 3000 pucerons.
Question 13
Simuler les cas suivants :
Pour cela modifier
Proposer une interprétation de chaque cas particulier simulés ci-dessus.
Cas général
Nous simulons désormais la dynamique H(x,y) = x + rx(1 −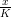 ) −
) −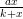 y pour trois états
initiaux différents. Nous rapellons que nous sommes toujours dans le cas d’ une fonction de
dommages linéaires.
y pour trois états
initiaux différents. Nous rapellons que nous sommes toujours dans le cas d’ une fonction de
dommages linéaires.
Les valeurs des paramètres sont
∙ δ = 0.302,
∙ a = 0.01,
∙ r = 2.10−2,
∙ K = 40 000,
∙ k = 100 000
∙état initial 1= 3 000 pucerons ≪ K,
∙état initial 2= 40 000 pucerons = K,
∙état initial 3= 80 000 pucerons ≫ K
Question 14
Simuler l’évolution du couple pucerons-coccinelles pour les trois valeurs de l’état initial ci-dessus. Interpréter chacune des simulations obtenues, et tirer une conclusion générale quant aux cas observés.
On définit Dnl par
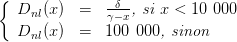 | (16) |
Les valeurs des paramètres sont
∙ δ = 0.302,
∙ a = 0.01,
∙ r = 2.10−2,
∙ K = 40 000,
∙ k = 100 000
Question 15 Effectuer les simulations pour les 2 états initiaux :
Commenter les graphiques obtenus.
Reprendre le cas d’une dynamique générale, d’une fonction de dommages non linéaires et d’un coût d’introduction quadratique, C(y) = (α + βy)2 par exemple. Observer le feedback optimal obtenu.
[1] C. Bidot. Modélisation et commande optimale de l’intéraction Coccinelle/Puceron dans le cadre de la lutte biologique. Rapport de stage INSA Toulouse, 2000.
[2] M. Duffaut. Modélisation d’un système proie prédateur dans le cadre de la lutte biologique. Rapport de stage INSA Toulouse, 2001.
[3] A. Maure Stratégies optimales pour la lutte biologique : application au couple pucerons-coccinelles Rapport de stage scientifique Ecole Nationale des Ponts et Chaussées, 2003.
[4] B. D’Andréa Novel & M. Cohen De Lara. Commande linéaire des systèmes dynamiques. Masson, 1993
[5] L. Edelstein-Keshet Mathematical models in biology. The Random house/Birkhauser mathematics series,1988.
[6] P.Faure. Analyse numérique, notes d’optimisation. ellipses,1988.
[7] A. Fera, H. Niknam, F. Kabiri, J-L. Picart, C. De Herce,J. Brun, G. Iperti & L. Lapchin The use of Harmonia axyridis larvae(coloptera : Coccinellidae) against Macropsiphum rosae(Hemiptera : Sternorrhyncha : Aphididae) on rose bushes., Eur.J.Entomol.93:59-67,1996
[8] R. Boll & E. Franco Protection des cultures sous abri au moyen de la lutte biologique,Journées du GRAB, 1998