Contents
Pour récupérer le code des exemples, utiliser les liens :
1 Allocation optimale en environnement constant (théorie)
1.1 Modèle d’optimisation en environnement constant
Dynamique
En suivant [1], on considère une plante annuelle qui croît et se reproduit selon la dynamique
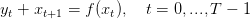 | (1) |
où
- T est le nombre de saisons (T < +∞) ;
- xt est la biomasse végétative au début de la saison t,
- yt est la biomasse reproductive produite au cours de la saison t.
Par des considérations biologiques et mathématiques assez générales, voici les hypothèses que
nous posons pour la fonction f de ressources assimilées, définie sur [0, +∞[ :
- f est de classe C2 sur ]0, +∞[ ;
- f(0) = 0 et f(x) > 0 pour x > 0 ;
- f est strictement croissante : f′ > 0 ;
- f est (strictement) concave : f′′≤ 0 (f′′ < 0).
Mortalité aléatoire
La plante a une durée de vie aléatoire 𝜃 de loi géométrique de paramètre β, probabilité de survie
:
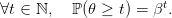 | (2) |
L’évènement {𝜃 = t} signifie que la plante meurt en fin de saison t.
Décisions et stratégies
Si, au début de la saison t, la plante a la biomasse végétative xt, elle assimile une biomasse totale
f(xt) dont elle peut arbitrer la répartition entre biomasse reproductive yt et future
biomasse végétative xt+1. La décision de la plante correspond au choix de répartition
entre biomasse reproductive et future biomasse végétative. On introduit la variable de
décision
![ut = xt+1 ∈ [0,f(xt)].](Plante_alloc_Q2x.png) | (3) |
Une stratégie pour la plante est une suite de décisions
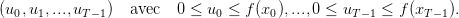 | (4) |
Critère
Dans ce modèle d’optimisation, une stratégie optimale pour la plante est une stratégie qui rend
maximale l’espérance du fitness (contribution individuelle aux générations futures), ici la
quantité de “rejetons” ou encore le cumul de la biomasse reproductive à la fin de l’année
:
![(T−∑ 1)∧𝜃
J (u(.)) = 𝔼 ( [f(xt) − ut]), u(.) = (u0,u1,...,uT− 1).
t=0](Plante_alloc_Q4x.png) | (5) |
L’espérance porte sur la variable aléatoire 𝜃, et un calcul simple montre que l’on peut faire
disparaître cette espérance :
![(T∑−1)∧𝜃 T∑− 1 T∑−1
J(u(.)) = 𝔼 ( [f(xt) − ut]) = 𝔼(1 {𝜃≥t}[f(xt) − ut]) = βt [f (xt) − ut],
t=0 t=0 t=0](Plante_alloc_Q5x.png) | (6) |
d’après (2).
Problème d’optimisation
Avec le calcul précédent, ce problème de croissance et reproduction optimales d’une plante se
formule alors :
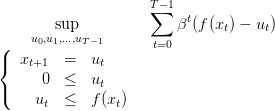 | (7) |
C’est un problème d’optimisation dynamique déterministe, à critère additif, avec
- coût instantané l(x,u,t) = βt(f(x) − u),
- coût final nul.
1.2 Résolution par la programmation dynamique
L’équation de Bellman s’écrit
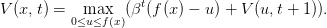 | (8) |
Si on pose
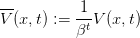 | (9) |
elle s’écrit également
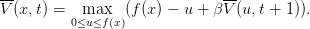 | (10) |
Les stratégies optimales u♯ sont données par
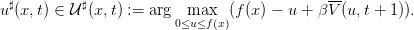 | (11) |
Question 1 Montrer que V (x,T −1) = f(x) et que la dernière commande optimale consiste
à investir toute la biomasse végétative en biomasse reproductive à T − 1, et donc à mourir
en T.
Comme V (x,T) = 0 (pas de coût final), on a
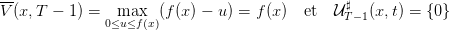
Fonction de croissance linéaire
On suppose ici que
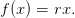 | (12) |
Question 2 Si βr ≤ 1, montrer que, pour t = 0,...,T − 1, V (x,t) = rx et 𝒰t♯(x,t) = 0.
Décrire alors le profil d’une trajectoire optimale.
Question 3 Si βr > 1, montrer que, pour t = 0,...,T − 1, V (x,t) = (β)T−trx et
𝒰t♯(x,t) = rx. Décrire alors le profil d’une trajectoire optimale.
Fonction de croissance strictement concave et de pente faible
On suppose ici que
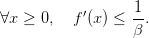 | (13) |
Question 4 Montrer que, pour t = 0,...,T − 1, V (x,t) = f(x) et 𝒰t♯(x,t) = 0. Décrire
alors le profil d’une trajectoire optimale.
Fonction de croissance strictement concave et de pente forte
On suppose ici que
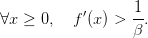 | (14) |
Question 5 Montrer que, pour t = 0,...,T − 1, 𝒰t♯(x,t) = f(x). Décrire alors le profil
d’une trajectoire optimale.
Fonction de croissance strictement concave et de pente modérée
On suppose ici que
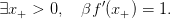 | (15) |
On note alors
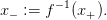 | (16) |
Question 6 Montrer qu’une règle optimale de décision au temps T − 2 est
- si la biomasse végétative est inférieure à x−, alors la biomasse totale (ressources
assimilées) sera entièrement transformée en biomasse végétative ;
- si la biomasse végétative est supérieure à x−, alors une partie de la biomasse totale
(ressources assimilées) sera transformée en biomasse végétative de manière à atteindre
précisement la taille x+, le reste étant transformé en biomasse reproductive.
On a
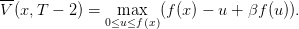
D’après les hypothèses sur f, la fonction u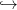 − u + βf(u) est strictement concave, avec un
maximum en u = x+. On en déduit aisément que
− u + βf(u) est strictement concave, avec un
maximum en u = x+. On en déduit aisément que
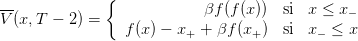
Question 7 Montrer que
- V (x,T −2) est continue et continûment dérivable en x = x−, et que β
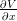 (x+,T −2) = 1
;
(x+,T −2) = 1
;
- V (x,T −2) est continûment dérivable et que
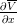 (x,T −2) est strictement décroissante.
(x,T −2) est strictement décroissante.
En déduire que la règle de décision optimale au temps t = T − 3, coïncide avec celle au temps
t = T − 2.
En continuant de la sorte, on montre qu’une stratégie optimale pour la plante en feedback sur
l’état consiste à suivre la règle suivante pour tout t = 0,...,T − 2.
- Si x ≤ x−, alors toutes les ressources sont dirigées vers la croissance, et la plante ne
donne aucun rejeton.
- Si x ≥ x−, alors la plante atteint précisément la taille x+ et transforme sa biomasse
restante en biomasse reproductive.
En t = T − 1, la décision optimale est de transformer toute la biomasse en biomasse reproductive.
2 Comparaison de stratégies en environnement constant (TP Scilab)
On prend
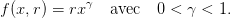 | (17) |
La commande est non plus ut ∈ [0,f(xt)], mais
![-ut---
vt := f(xt) ∈ [0,1 ] (vt = 0 si f (xt) = 0)](Plante_alloc_Q23x.png) | (18) |
2.1 Dynamique de la plante
Ouvrir un fichier TP_plante_1.sci et y écrire une fonction Scilab dyn_plante représentant la
fonction de croissance, en fonction de l’état x (la valeur du paramètre r sera donnée plus
tard).
function b=dyn_plante(x)
b=r*x^{puis} endfunction
Dans le fichier TP_plante_1.sci , écrire la fonction dyn_plante_com.
function b=dyn_plante_com(x,v,s)
if v < 0 | v > 1 then
b='ERREUR : commande au-delà des bornes'
else if s==0 then b=0
else b=v*dyn_plante(x) end end endfunction
2.2 Fonctions de coût
Dans le fichier TP_plante_1.sci, écrire les fonctions de coût instantané et de coût final
suivantes.
function cout=rejetons(etat,commande,temps) cout=(1-commande)*beta^{temps}*dyn_plante(etat);
endfunction function cout=cout_fin_zero(etat,temps) cout=0; endfunction
2.3 Comparaison entre stratégies
Exemples de stratégies
Dans le fichier TP_plante_1.sci, écrire les fonctions Scilab suivantes :
- strategie_M (M pour mourir) qui représente la stratégie “se reproduire et mourir” :
la sortie de strategie_M est 0 ;
- strategie_R (R pour random) qui représente une stratégie aléatoire : la sortie de
strategie_R est un réel aléatoire dans [0, 1] ;
- strategie_C (C pour croître) qui représente la stratégie “croître sans se reproduire
sauf au dernier pas de temps de commande” : la sortie de strategie_C est soit 0 (se
reproduire et mourir) soit 1 (croître sans se reproduire).
function v=strategie_M(x,t) v=0 endfunction function v=strategie_R(x,t)
v=rand() endfunction function v=strategie_C(x,t) if t < T then
v=1 else v=0 end endfunction
Fonctions Scilab pour le calcul de trajectoires
Dans le fichier TP_plante_1.sci, écrire la fonction Scilab traj_feedback suivante, qui a pour
arguments
- un état initial,
- une fonction Scilab dynamique_commandee (sur le modèle de dyn_plante_com),
- une fonction Scilab feedback (sur le modèle de strategie_X),
- un aléa (ici, à deux composantes, aléa de survie et aléa de ressources)
et qui donne, avec ce feedback, les trajectoires correspondantes d’état et de commande.
function [x,v]=traj_feedback(etat_initial,dynamique_commandee,feedback,alea)
horizon=size(alea,2);
x=etat_initial v=[] for t=1:horizon do
v=[v,feedback(x($),t)]
x=[x,dynamique_commandee(x($),v($),alea(t))]
end endfunction
Dans le fichier TP_plante_1.sci, écrire la fonction Scilab cout_total suivante, qui a pour
arguments
- trajectoire, une trajectoire d’état, c’est-à-dire un vecteur de dimension (1,T + 1)
- commande, une trajectoire de commande, c’est-à-dire un vecteur de dimension (1,T)
- une fonction Scilab cout_inst,
- une fonction Scilab cout_fin,
et qui retourne la valeur du critère additif le long des trajectoires d’état et de commande.
function cout=cout_total(trajectoire,commande,cout_inst,cout_fin)
horizon=prod(size(commande)) if 1+horizon <> prod(size(trajectoire)) then
cout='ERREUR : dim(trajectoire) différent de 1+dim(commande)'
else cout=[] for t=1:horizon do
cout=[cout,cout($)+cout_inst(trajectoire(t),commande(t),t)]
end cout=[cout,cout($)+cout_fin(trajectoire(1+horizon),1+horizon)] end endfunction
Fonction de croissance linéaire
Ouvrir un fichier TP_plante_1.sce et y recopier les paramètres suivants.
puis=1; beta=0.9,
r=1.2; T=10; x0=1;
Question 8 Calculer les trajectoires d’état et de commande du système en boucle
fermée avec les différentes stratégies strategie_X. On utilisera pour cela la fonction
Scilab traj_feedback.
Calculer les trajectoires de fitness correspondantes. On utilisera pour cela la fonction
Scilab cout_total,
Tracer les trajectoires d’état, de commande et de fitness à l’aide de la commande
Scilab plot2d2.
Écrire ces instructions dans le fichier TP_plante_1.sce, et l’exécuter par la commande
Scilab exec(’TP_plante_1.sce’).
getf('TP_plante_1.sci'); strategie=list(); strategie(1)=strategie_M; strategie(2)=strategie_R;
strategie(3)=strategie_C; correspondance=list(); correspondance(1)=string("mourir");
correspondance(2)=string("aleatoire"); correspondance(3)=string("croitre");
etat_initial=1; dynamique=dyn_plante_com;
alea=ceil(beta-rand(1,T));
cout_inst=rejetons; cout_fin=cout_fin_zero; for i=1:3 do
[b,v]=traj_feedback(etat_initial,dynamique,strategie(i),alea); f=cout_total(b,v,cout_inst,cout_fin);
xset("window",3*(i-1));xbasc();plot2d2(1:T+1,f,rect = [0,0,T+2,max(f)+1]);
xtitle("stratégie "+correspondance(i)+" : fitness");
xset("window",3*(i-1)+1);xbasc();plot2d2(1:T,v,rect = [0,0,T+1,max(v)+1]);
xtitle("stratégie "+correspondance(i)+" : commande");
xset("window",3*(i-1)+2);xbasc();plot2d2(1:T+1,b,rect = [0,0,T+2,max(b)+1]);
xtitle("stratégie "+correspondance(i)+" : état");
printf("la fitness totale pour la strategie "+correspondance(i)+" est : %"+" f\n",f($))
halt(); xdel((3*(i-1)):(3*(i-1)+2)); end
Question 9 Comparer le fitness total pour les différentes stratégies.
Fonction de croissance strictement concave
On prend ici
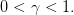 | (19) |
Question 10 Donner les expressions analytiques de x+ et x−, introduits respectivement aux
équations (15) et (16). Écrire en Scilab les formules correspondantes xp et xm.
puis=0.5; xp=(beta*r*puis)^{1/(1-puis)}; xm=(xp/r)^{1/puis};
Question 11 Dans le fichier TP_plante_1.sci, écrire une une fonction Scilab strategie_O (
_O pour optimale), d’arguments un état x et un temps t, de sortie la commande v répondant à la
stratégie (feedback) suivante de plante :
- si la biomasse végétative est strictement inférieure à x−, alors ne pas se reproduire ;
- si la biomasse végétative est supérieure ou égale à x−, alors au temps suivant elle sera
égale à x+.
Vérifier, à partir des résultats théoriques vus plus haut, que cette stratégie est optimale.
function v=strategie_O(x,t) if x < xm then v=1 else
v=xp/dyn_plante(x) end endfunction
Question 12 Reprendre les questions précédentes.
strategie(4)=strategie_O; correspondance(4)=string("optimale");
Question 13 Que constate-t-on en faisant varier γ ?
P=0.1:0.2:0.9; for j=1:prod(size(P)) do puis=P(j);
xp=(beta*r*puis)^{1/(1-puis)}; xm=(xp/r)^{1/puis}; x0=xm/10;
printf("gamma=%"+" f\n",P(j)); for i=1:4 do
[y,v]=traj_feedback(x0,dynamique,strategie(i),alea); f=cout_total(y,v,cout_inst,cout_fin);
printf("la fitness totale pour la strategie "+correspondance(i)+" est : %"+" f\n",f($)) end end
3 Calcul de stratégies optimales en environnement constant (TP Scilab)
On prend ici
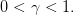 | (20) |
3.1 Paramètres
Recopier les paramètres suivants dans un fichier TP_plante_2.sce.
T=10; beta=0.9; r=1.2; puis=0.5;
3.2 Discrétisation de l’état, de la commande et des coûts
Recopier le code suivant dans le fichier TP_plante_2.sce ; il donne la discrétisation de l’état et de
la commande, ainsi que le coût instantané et le coût final. On pourra consulter le document
Programmation dynamique, macros générales.
etat=[0:(xm/6):(1.2*xp)]; commande=0:0.05:1; rejetons=list();
actualisation=cumprod([1,beta*ones(1,T-1)]); for l=1:prod(size(commande)) do
rejetons(l)=(1-commande(l))*(r*(etat')^{puis})*actualisation;
end cout_fin_zero=zeros(etat');
On notara qu’on redéfinit, et donc écrase, des fonctions Scilab définies plus haut.
3.3 Discrétisation de la dynamique et passage en matrices de transition
Récupérer les fonctions Scilab predec_sucess, egal et discretisation du document
Programmation dynamique, macros générales et les copier dans le fichier TP_plante_2.sci, ainsi
que la fonction suivante.
function b=dyn_plante_com(x,v)
b=v*r*x^{puis} endfunction
Recopier le code suivant dans le fichier TP_plante_2.sce.
getf('TP_plante_2.sci') dynamique_commandee=dyn_plante_com;
matrice_transition=discretisation(etat,commande,dynamique_commandee);
Question 14 Vérifier que la liste de matrices matrice_transition est bien formée de
matrices de transition, c’est-à-dire à coefficients positifs ou nuls, et dont la somme de chaque
ligne vaut 1.
cardinal_commande=size(matrice_transition); for l=1:cardinal_commande do
sum(matrice_transition(l),"c")' mini(matrice_transition(l))
maxi(matrice_transition(l)) halt(); end
3.4 Résolution numérique par programmation dynamique
Récupérer les fonctions Scilab Bell_stoch et trajopt du document Programmation dynamique,
macros générales et les copier dans le fichier TP_plante_2.sci.
Recopier ensuite le code suivant dans le fichier TP_plante_2.sce.
cout_instantane=rejetons; cout_final=cout_fin_zero;
[valeur,feedback]=Bell_stoch(matrice_transition,cout_instantane,cout_final);
etat_initial=grand(1,1,'uin',2,prod(size(etat)));
z=trajopt(matrice_transition,feedback,cout_instantane,cout_final,etat_initial);
zz=list(); zz(1)=etat(z(1));
zz(2)=commande(z(2)); zz(3)=z(3);
xset("window",1);xbasc();plot2d2(1:prod(size(zz(1))),zz(1));xtitle("taille")
xset("window",2);xbasc();plot2d2(1:prod(size(zz(2))),zz(2));xtitle("commande")
xset("window",3);xbasc();plot2d2(1:prod(size(zz(3))),zz(3));xtitle("fitness")
Question 15 Examiner les trajectoires, et les comparer avec celles obtenues précédemment.
4 Allocation optimale en environnement aléatoire (théorie)
4.1 Modèle d’optimisation en environnement aléatoire
On étend le modèle en environnement constant introduit ci-dessus en modèle en environnement
stochastique comme suit. On suppose que
- la biomasse totale à allouer au cours d’une saison est à présent fonction des ressources
r du milieu, de sorte que la la fonction x
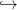 f(x) est remplacée par une fonction
x
f(x) est remplacée par une fonction
x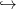 f(x,r) qui possède les mêmes propriétés ;
f(x,r) qui possède les mêmes propriétés ;
- au cours de la saison t, les ressources du milieu sont une variable aléatoire Rt prenant
ses valeurs dans un ensemble fini {r1,...,rm} ;
- les variables aléatoires R0,...,RT−1 forment une chaîne de Markov : on note π la matrice
de terme général π(i,j) = ℙ(Rt+1 = rj|R
t = ri) ;
- à la saison t, les réalisations des variables aléatoires R0,...,Rt sont observables par la
plante.
À présent, la stratégie v0,...,vT−1 est en feedback sur l’état double (xt,Rt) : vt dépend en particulier de
R0,..., Rt qui sont observés.
Dynamique stochastique
La dynamique stochastique de la plante est la suivante : partant de la taille x ∈ ℝ+
et de l’environnement ri, avec la commande v ∈ [0, 1], à la saison suivante la plante
- meurt, i.e. transite vers la taille 0, avec probabilité 1 − β ;
- transite vers la taille vf(x,rj) avec probabilité βπ(i,j).
Commande
Pour des commodités de programmation (bornes fixes sur la commande), on a modifié la
commande (0 ≤ v ≤ 1) par rapport à la précédente version (0 ≤ u ≤ f(x)). La commande v est ici
la fraction de la ressource aléatoire allouée à la biomasse végétative.
Stratégies en feedback sur l’état
Une stratégie optimale pour la plante est une stratégie qui rend maximum l’espérance du fitness
(contribution individuelle aux générations futures), ici la quantité de “rejetons” ou encore le cumul
de la biomasse reproductive à la fin de l’année :
![T∑− 1 T
J(v(.)) = 𝔼( (1 − vt)f(xt,Rt)) avec v(.) = (v0,...,vT−1) ∈ [0, 1] .
t=0](Plante_alloc_Q28x.png) | (21) |
On peut noter que l’espérance est ici une somme finie.
4.2 Résolution par la programmation dynamique
L’équation de Bellman s’écrit
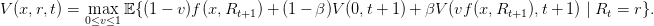 | (22) |
Question 16 Montrer par récurrence que V (0,t) = 0, de sorte que
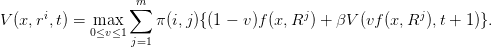 | (23) |
5 Calcul de stratégies optimales en environnement aléatoire (TP Scilab)
On prend f(x,r) comme en (17), c’est-à-dire
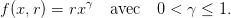 | (24) |
Ce dernier chapitre comporte moins d’explications que les précédents. En revanche, le code
Scilab est abondamment commenté.
5.1 Discrétisation du problème
Dans ce deuxième modèle, l’état n’est plus comme avant seulement la taille x ∈ ℝ+, mais un
couple taille – environnement (x,r) ∈ ℝ+ ×{r1,...,rm}.
Tout d’abord, nous discrétisons l’espace ℝ+ en {x1,...,xn}, où x1 correspond à x = 0 (plante
morte) et xn est une taille maximale pour la plante. Nous discrétisons également la fonction
(x,r,v)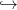 vf(x,r) en une fonction
vf(x,r) en une fonction
![F : {x1, ...,xn } × {r1,...,rm} × [0,1] → {x1, ...,xn }.](Plante_alloc_Q33x.png) | (25) |
Ensuite, nous exprimons la dynamique stochastique vue plus haut par le biais d’une famille,
indicée par la commande v, de probabilités de transition Mv sur l’ensemble produi fini
{x1,...,xn}×{r1,...,rm}.
5.2 Première expression des transitions à l’aide d’hypermatrices
Le code Scilab qui suit exprime ces probabilités de transition Mv par le biais d’hypermatrices à
quatre indices. Une hypermatrice est une extension à plus de deux indices des matrices sous
Scilab.
Le vecteur taille est formé des éléments de la suite (x1,...,xm) des valeurs de la première
composante discrétisée de l’état: taille(i) = xi, i = 1,...,m.
5.2.1 Transitions de l’environnement
Le vecteur env est formé des éléments de la suite (r1,...,rm) des valeurs possibles prises par les
ressources : env(i) = ri, i = 1,...,m.
Dans le fichier TP_plante_2.sci, recopier le code suivant.
function pi=tr_env_auc_cor_unif(cardinal_alea)
dd=cardinal_alea
pi=1/dd*ones(dd,dd) endfunction function pi=tr_env_cor_proche_vois(cardinal_alea)
dd=cardinal_alea
pi=diag([0.5,1/3*ones(1:(dd-2)),0.5])+diag([0.5,1/3*ones(1:(dd-2))],1)+ ...
diag([1/3*ones(1:(dd-2)),0.5],-1) endfunction
function pi=tr_env_cor_crois(cardinal_alea,rho)
dd=cardinal_alea
pi=diag([rho*ones(1:(dd-1)),1])+diag([(1-rho)*ones(1:(dd-1))],1) endfunction
function pi=tr_env_cor_decrois(cardinal_alea,rho)
dd=cardinal_alea
pi=diag([1,rho*ones(1:(dd-1))])+diag([(1-rho)*ones(1:(dd-1))],-1) endfunction
function pi=tr_env_cor_et_chute(cardinal_alea,rho)
dd=cardinal_alea
pi=diag([rho*ones(1:dd)]) pi(2:$,1)=1-rho pi(1,2)=1-rho
endfunction function pi=tr_env_cor_et_ascension(cardinal_alea,rho)
dd=cardinal_alea
pi=diag([rho*ones(1:dd)]) pi(1:$,$)=1-rho pi(dd,dd-1)=1-rho endfunction
5.2.2 Transitions de l’état (taille,environnement)
Dans le fichier TP_plante_2.sci, recopier le code suivant.
function Hypermatrices=constr_HyperM(taille,env,commande,pi,dynamique_commandee)
dims=[prod(size(taille)),prod(size(env))]; ddims=[dims(1),dims(1),dims(2),dims(2)];
Hypermatrices=list(); cardinal_commande=prod(size(commande));
cardinal_taille=prod(size(taille)); for l=1:cardinal_commande do
Hypermat=hypermat([ddims]);
for y=1:dims(2) do image=dynamique_commandee(taille,y,commande(l));
indices_image_discretisee=predec_sucess(taille,image);
indices1=indices_image_discretisee(1); indices2=indices_image_discretisee(2);
probabilites=indices_image_discretisee(3); M1=zeros(cardinal_taille,cardinal_taille);
M2=zeros(M1); for i=1:cardinal_taille do
M1(i,indices1(i))=probabilites(i); M1(i,indices2(i))=1-probabilites(i);
end for z=1:dims(2) do Hypermat(:,1,y,z)=(1-beta)*pi(y,z);
Hypermat(:,:,y,z)=Hypermat(:,:,y,z)+(M1+M2)*beta*pi(y,z); end
end
Hypermatrices(l)=Hypermat end endfunction
5.3 Opérations de conversion pour s’adapter à la fonction Scilab Bell_stoch
La fonction Scilab Bell_stoch de résolution numérique de l’équation de la programmation
dynamique stochastique est écrite pour une chaîne de Markov sur {1,2...,taille_etat}
(on obtient en effet un algorithme performant en confondant un état et un indice d’un
vecteur).
C’est pourquoi, les hypermatrices de transition à quatre indices seront transformées en matrices
ordinaires à deux indices en “déroulant” les indices. Par exemple, une matrice (qui est un cas
particulier d’hypermatrice) 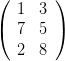 sera déroulée en (1, 7, 2, 3, 5, 8).
sera déroulée en (1, 7, 2, 3, 5, 8).
C’est ainsi que l’espace des états à deux dimensions peut être représenté comme un espace
d’état à une dimension. À un couple (x,r) ∈{x1,...,xn}×{r1,...,rm} est associé l’état
e ∈{1,...,n × m}. On résout le problème d’optimisation avec cet espace d’état intermédiaire (à
une dimension), puis on repasse dans l’espace d’état (taille, environnement) à deux dimensions
d’origine.
Question 17 Dans le fichier TP_plante_2.sci, recopier le code suivant dans lequel on
définit des macros de conversion.
function Matrices=conv_HyperM(Hypermatrices)
dd=size(Hypermatrices(1)) dims=[dd(1),dd(3)] Matrices=list()
for i=1:prod(size(commande)) do Mat=[] for j=1:dims(2) do if dims(2) <> 1 then
a=Hypermatrices(i)(:,:,j,:).entries b=matrix(a,dims(1),prod(dims))
else b=matrix(Hypermatrices(i)(:,:,j,:),dims(1),prod(dims)) end
Mat=[Mat;b]
end
Matrices(i)=full(Mat) end endfunction function n=convert1(i,j,dims)
if i > dims(1) | j > dims(2) then n='i ou j > dims' else
n=(j-1)*dims(1)+i; end endfunction function [i,j]=convert2(n,dims)
i=modulo(n,dims(1))
ind=find(i==0) i(ind)=dims(1) j=int(n/dims(1))+1 ind2=find((dims(1))\n==int((dims(1))\n))
jj=(dims(1))\n j(ind2)=jj(ind2) endfunction function Hmat=convert2_mat(matrice,dims)
Hmat=hypermat([dims,T-1]) n=1:prod(dims) [i,j]=convert2(n,dims) for t=1:T-1 do
for indice=1:prod(dims) do Hmat(i(indice),j(indice),t)=matrice(n(indice),t) end
end endfunction function cout_instantane=conv_cout(taille,env,commande,cout,horizon)
dims=[prod(size(taille)),prod(size(env))]
cout_instantane=list() for j=1:prod(size(commande)) do cout_i=[]
for t=1:horizon do cout_it=hypermat(dims,sparse([],[],[dims(1),dims(2)]));
for etat1=1:dims(1) do for etat2=1:dims(2) do
cout_it(etat1,etat2)=cout(taille(etat1),env(etat2),commande(j),t)
end end cout_it=matrix(cout_it,1,prod(dims))
cout_i=[cout_i(cout_it)']
end cout_instantane(j)=full(cout_i) end endfunction
5.4 Transitions et coûts adaptés à la fonction Scilab Bell_stoch
Ouvrir un fichier TP_plante_3.sce et y recopier le code suivant.
getf('TP_plante_2.sci'); T=10; beta=0.9; rr=1.2; puis=0.5;
xp=(beta*rr*puis)^{1/(1-puis)}; xm=(xp/rr)^{1/puis}; taille=[0:(xm/3):(1.2*xp)];
env=[0.6,0.8,1,1.2,1.4]; commande=0:0.05:1;
cardinal_env=prod(size(env)); cardinal_taille=prod(size(taille));
pi=tr_env_auc_cor_unif(cardinal_env);
function b=dyn_plante_com(x,r,v)
b=v*r*x^{puis} endfunction dynamique_commandee=dyn_plante_com;
Hypermatrices=constr_HyperM(taille,env,commande,pi,dynamique_commandee);
matrice_transition=conv_HyperM(Hypermatrices); function ci=rejetons2(taille,env,commande,temps)
ci=(1-commande)'*env*taille^(puis)*beta^{temps-1}
ind=find(taille==1),ci(ind)=0 endfunction rejetons=conv_cout(taille,env,commande,rejetons2,T);
cout_fin_nul=zeros(cardinal_env*cardinal_taille,1);
Question 18 Vérifier que la liste de matrices matrice_transition est bien formée de
matrices de transition, c’est-à-dire à coefficients positifs ou nuls, et dont la somme de chaque
ligne vaut 1.
5.5 Simulation de trajectoires bouclées avec le feedback optimal
Les fonctions nécessaires à la résolution du problème de Bellman et à l’obtention de trajectoires
étant à présent écrites dans le fichier TP_plante_2.sci, recopier le code suivant dans le fichier
TP_plante_3.sce.
dims=[cardinal_taille,cardinal_env]; stacksize(3000000);
cout_instantane=rejetons; cout_final=cout_fin_nul;
[valeur,feedback]=Bell_stoch(matrice_transition,cout_instantane,cout_final);
indice_taille_init=grand(1,1,'uin',2,cardinal_taille); indice_env_init=grand(1,1,'uin',1,cardinal_env);
etat_initial=convert1(indice_taille_init,indice_env_init,dims);
z=trajopt(matrice_transition,feedback,cout_instantane,cout_final,etat_initial);
[indice_taille,indice_env]=convert2(z(1),dims)
x=taille(indice_taille); e=env(indice_env);
xset("window",1);xbasc();plot2d2(1:prod(size(x)),x); xtitle("taille")
xset("window",2);xbasc();plot2d2(1:prod(size(e)),e,rect = [0,0,T+1,max(e)+1]); xtitle("environnement")
xset("window",3);xbasc();plot2d2(1:prod(size(commande(z(2)))),commande(z(2)));
xtitle("commande") xset("window",4);xbasc();plot2d2(1:prod(size(z(3))),z(3)); xtitle("fitness")
Question 19 Effectuer différentes simulations. Changer notamment de matrice pi.
References
[1] S. Amir and D. Cohen. Optimal reproductive efforts and the timing of reproduction
of annual plants in randomly varying environments. Journal of Theoretical Biology,
147:17–42, 1990.
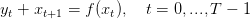
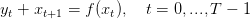
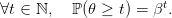
![ut = xt+1 ∈ [0,f(xt)].](Plante_alloc_Q2x.png)
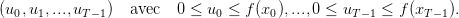
![(T−∑ 1)∧𝜃
J (u(.)) = 𝔼 ( [f(xt) − ut]), u(.) = (u0,u1,...,uT− 1).
t=0](Plante_alloc_Q4x.png)
![(T∑−1)∧𝜃 T∑− 1 T∑−1
J(u(.)) = 𝔼 ( [f(xt) − ut]) = 𝔼(1 {𝜃≥t}[f(xt) − ut]) = βt [f (xt) − ut],
t=0 t=0 t=0](Plante_alloc_Q5x.png)
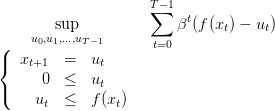
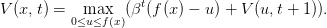
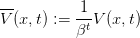
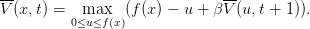
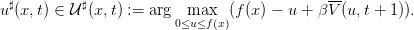
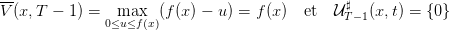
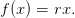
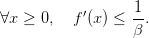
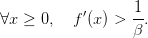
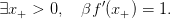
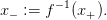
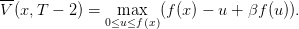
 − u + βf(u) est strictement concave, avec un
maximum en u = x+. On en déduit aisément que
− u + βf(u) est strictement concave, avec un
maximum en u = x+. On en déduit aisément que
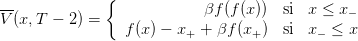
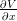 (x+,T −2) = 1
;
(x+,T −2) = 1
;
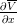 (x,T −2) est strictement décroissante.
(x,T −2) est strictement décroissante.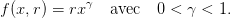
![-ut---
vt := f(xt) ∈ [0,1 ] (vt = 0 si f (xt) = 0)](Plante_alloc_Q23x.png)
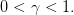
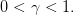
 f(x) est remplacée par une fonction
x
f(x) est remplacée par une fonction
x f(x,r) qui possède les mêmes propriétés ;
f(x,r) qui possède les mêmes propriétés ;
![T∑− 1 T
J(v(.)) = 𝔼( (1 − vt)f(xt,Rt)) avec v(.) = (v0,...,vT−1) ∈ [0, 1] .
t=0](Plante_alloc_Q28x.png)
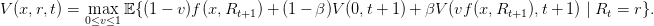
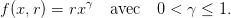
 vf(x,r) en une fonction
vf(x,r) en une fonction
![F : {x1, ...,xn } × {r1,...,rm} × [0,1] → {x1, ...,xn }.](Plante_alloc_Q33x.png)
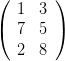 sera déroulée en (1, 7, 2, 3, 5, 8).
sera déroulée en (1, 7, 2, 3, 5, 8).