Management of a Renewable Ressource. Deterministic and Robust Cases

Michel De Lara & Luc Doyen
(last modification date: October 10, 2017)
Version pdf de ce document
Version sans bandeaux

1 Problem statement
2 Deterministic growth
3 Uncertain growth

Contents

1 Problem statement
2 Deterministic growth
 2.1 Try your own strategy
 2.2 Intertemporal discounted utility maximization
 2.3 Minimal utility maximization or Rawls criterion
 2.4 Tolerable window and guaranteed harvesting (viability)
 2.5 Intertemporal utility maximization under tolerable window and guaranteed harvesting
 2.6 Minimal utility maximization or Rawls criterion under tolerable window and guaranteed harvesting
3 Uncertain growth
 3.1 Worst intertemporal utility maximization
 3.2 Worst minimal utility maximization
 3.3 Tolerable window and guaranteed harvesting (robust viability)

1 Problem statement

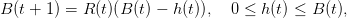
Consider a renewable ressource whose stock, measured through its biomass B, is considered globally, as one single unit, without any consideration for the structure population. Its growth is materialized through the linear Schaefer model

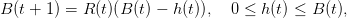B(t + 1) = R (t)(B (t) − h(t)), 0 ≤ h (t) ≤ B (t),
(1)

where h(t) is the harvesting at time t and R(t) = 1 + r(t) is the productivity of the resource.

Adapted from [1, p. 258], we shall illustrate the results with the Antartic baleen whale example as in Table 1.

Antartic baleen whale
intrinsic growth r = 5%
carrying capacity K = 400 000 BWH
catchability q = 0.0 016 WCY
price p = 7 000 $ per BWU
cost c = 600 000 $ per WCY

Table 1: Antartic baleen whale data for a discrete time logistic model (adapted from [1, p. 258]). BWH: blue whale unit. WCY: whale-catcher year.

2 Deterministic growth

In this case, the productivity is stationary and deterministic:

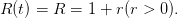R (t) = R = 1 + r(r > 0).
(2)

2.1 Try your own strategy

Question 1 You have to manage the whale population whose dynamics parameters are given in Table 1. Design your own catch strategy Catch(t,B) (following the model of the random catch effort strategy in the scilab code below). Give the scilab code corresponding to your own catch strategy. Draw simulations of biomass and catch trajectories.

  R_whale=1.05;// per capita productivity
  R=R_whale;
  K_whale=400000;// carrying capacity
  K=K_whale;
  
  // LINEAR DYNAMICS
  function y=linear(B) y=R*B,endfunction;
  
  // RANDOM CATCH EFFORT 
  function h=rand_effort(t,B) h=rand()*B,endfunction;
  
  Horizon=10;
  years=1:Horizon;
  yearss=1:(Horizon+1);
  yearsss=1:(Horizon+2);
  
  Binit=K/2;
  // initial condition
  trajectory_whale=zeros(yearss);
  // vector will contain the trajectory B(1),...,B(Horizon+1)
  catch_whale=zeros(years);
  // vector will contain the catches h(1),...,h(Horizon)
  trajectory_whale(1)=Binit;
  // initialization of vector B(1),...,B(Horizon+1)
  for t=years do
    catch_whale(t)=rand_effort(t,trajectory_whale(t));
    trajectory_whale(t+1)=linear(trajectory_whale(t)-catch_whale(t));
  end;
  
  // Graphics 
  xset("window",20+1);xbasc(20+1);
  plot2d2(yearss,[trajectory_whale;[catch_whale,0]]');
  xtitle('Trajectory under linear growth with R='+string(R_whale)+' and random effort', ...
         'year (t)','biomass (t)')
  legends(['Biomass trajectory';'Catch trajectory'],[1,2],'ur');

2.2 Intertemporal discounted utility maximization

We now assume that some planner aims at maximizing the sum of discounted utilities of the catches plus a final stock utility. The maximization problem is

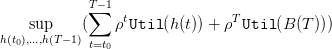T∑−1 sup ( ρtUtil (h(t)) + ρT Util (B (T ))) h(t0),...,h(T− 1) t=t0
(3)

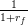where ρ = 1+1r- f ∈ [0, 1] is a discount factor and Util(⋅) is a utility function, concave and strictly increasing on ℝ+. Notice that the final term Util(B(T)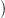) corresponds to an existence or inheritance value of the stock. We shall use a discount factor ρ with typical values ranging between 0.9 and 1. We restrict the study to the isoelastic utility case where

Util(h ) = h η with 0 < η < 1.
(4)

Analytic resolution by dynamic programming

The dynamic programming equation is:

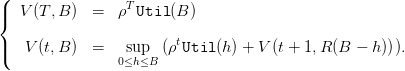(| V (T,B ) = ρT Util (B ) { t |( V (t,B ) = 0≤suhp≤B (ρ Util (h) + V(t + 1,R (B − h))).
(5)

By backward induction, it can be proved that

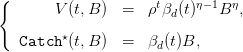{ V (t,B ) = ρtβd (t)η−1B η, ⋆ Catch (t,B ) = βd(t)B,
(6)

where βd(t) is given by the backward equation

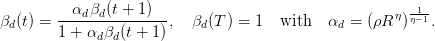βd(t) = --αdβd(t-+-1)--, βd(T ) = 1 with αd = (ρR η)η1−1. 1 + αdβd(t + 1)
(7)

It can be deduced that, along the optimal path given by

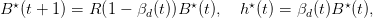B ⋆(t + 1) = R (1 − βd (t))B ⋆(t), h⋆(t) = βd (t)B ⋆(t),
(8)

we have

h⋆(t +-1) 11−η h⋆(t) = (ρR ) .
(9)

scilab simulations

Question 2 Simulate optimal catches and biomass trajectories (B⋆(t),h⋆(t)). Change the value of the discount factor ρ to modify the location of ρR with respect to 1. Do at least three cases with ρR > 1, ρR = 1 and ρR < 1. What do you observe?

  Binit=K/2;
  eta=0.5;
  rho=1/(1+0.03);
  alpha=(rho*R^eta)^{1/(eta-1)}
  
  b=[];
  b(Horizon+1)=1;
  for t=Horizon:-1:1 do
    b(t)=alpha*b(t+1)/(1+alpha*b(t+1));
  end;
  
  // Optimal catches and biomass
  
  Bopt=[];
  hopt=[];
  Bopt(1)=Binit;
  for t=1:Horizon do
    hopt(t)=b(t)*Bopt(t);
    Bopt(t+1)=R*(Bopt(t)-hopt(t));
  end;
  
  // Graphic display
  xbasc();xset('window',20+2);
  plot2d2(yearss,[[hopt;Bopt($)],[Bopt]])
  // plot2d2(yearsss, [[hopt; Bopt($); 0] [Bopt;0]])
  xtitle('Intertemporal utility maximization '+'with rho*R = '+string(rho*R),'years', ...
         'biomass')
  legends(['Optimal catches';'Optimal biomass'],[1,2],'ul');

Question 3 What is the influence of η on the optimal paths (B⋆(t),h⋆(t))? In particular, what happens when η ≈ 1? Comment knowing that 1 − η may be interpreted as the constant relative risk aversion of the decision-maker.

Question 4 Write a program which evaluates the criterion

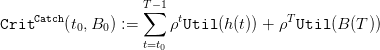T∑− 1 CritCatch(t ,B ) := ρtUtil(h (t)) + ρTUtil (B (T )) 0 0 t=t0
(10)

for any catch decision rule Catch : (t,B)↦→Catch(t,B) (admissible in the sense that 0 ≤ Catch(t,B) ≤ B), and where

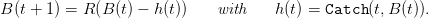B (t + 1) = R(B (t) − h (t)) with h(t) = Catch (t,B (t)).
(11)

Compare the criterion values given by

Question 5 Write a program which computes for any harvesting strategy Catch(t,B)

Plot and compare the profit trajectories t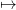↦→profit(t) given by

2.3 Minimal utility maximization or Rawls criterion

We now assume that the planner aims at sustainability and intergenerational equity, and attempts at maximizing the utility of the “poorest” generation. The maximization problem is then

sup min ( min Util (h(t)),Util (B (T))). h(t0),...,h(T− 1) t=t0,...,T −1
(14)

Analytic resolution by dynamic programming

The dynamic programming equation is:

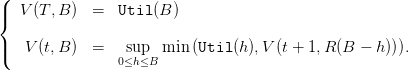( |{ V (T, B ) = Util (B ) |( V (t,B ) = sup min (Util (h),V (t + 1,R (B − h ))). 0≤h≤B
(15)

By backward induction, it can be proved that

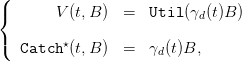( { V (t,B ) = Util(γd(t)B ) ( Catch ⋆(t,B ) = γd(t)B,
(16)

where γd(t) is given by the backward equation

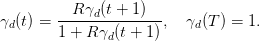--Rγd(t-+-1)--- γd(t) = 1 + Rγd(t + 1), γd(T ) = 1.
(17)

Consequently, along the maximin optimal path given by

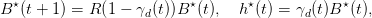⋆ ⋆ ⋆ ⋆ B (t + 1) = R (1 − γd(t))B (t), h (t) = γd(t)B (t),
(18)

we have

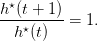h⋆(t +-1) h⋆(t) = 1.
(19)

scilab simulations

Question 6 Adapt the previous scilab code to obtain the maximin path (B⋆(t),h⋆(t)).

Question 7 Compare the trajectories of the maximin criterion, of the stock biomasses and of the catches between

2.4 Tolerable window and guaranteed harvesting (viability)

We assume that the policy is to constrain the biomass level within an ecological window, namely between conservation and maximal safety values:

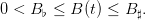0 < B♭ ≤ B (t) ≤ B♯.
(20)

A minimal catch is also required:

0 < h♭ ≤ h(t).
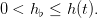(21)

Analytic resolution by dynamic programming

The dynamic programming equation for the viability kernels is:

( { V iab(T) = [B♭,B ♯], ( V iab(t) = {B ∈ [B ♭,B♯] | ∃h ∈ [h♭,B], R (B − h) ∈ V iab(t + 1)}.
(22)

Question 8 Define by backward induction

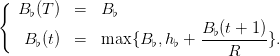
{ B (T) = B ♭ ♭ B ♭(t) = max {B ♭,h♭ + B♭(t +-1-)}. R

Show that, whenever B♭(t) ≤ B♯, the viability kernels are intervals:

V iab(t) = [B ♭(t),B ♯].

Show that the viable decision rules Catch(t,B) are those which belong to

[h♭(t,B),h ♯(t,B )] := [B − B-♯,B − B-♭(t +-1)]. R R

scilab simulations

Question 9 Fix a guaranteed yield h♭ as a fraction of carrying capacity K. Simulate trajectories with different viable decision rules.

2.5 Intertemporal utility maximization under tolerable window and guaranteed harvesting

The maximization problem is

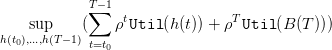T−1 ∑ t T h(t ),s..u.,ph(T− 1)( ρUtil (h(t)) + ρ Util (B (T ))) 0 t=t0
(23)

under the contraints

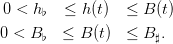
0 < h♭ ≤ h(t) ≤ B (t) 0 < B♭ ≤ B(t) ≤ B ♯.

The dynamic programming equation is:

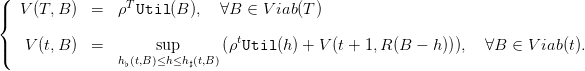( T |{ V(T, B ) = ρ Util(B ), ∀B ∈ V iab (T ) t |( V (t,B ) = sup (ρ Util (h) + V(t + 1,R (B − h))), ∀B ∈ V iab(t). h♭(t,B )≤h≤h ♯(t,B)
(24)

Question 10 Adapt the result and the associated scilab code to compute optimal viable paths (B⋆(t),h⋆(t)).

2.6 Minimal utility maximization or Rawls criterion under tolerable window and guaranteed harvesting

The maximization problem is

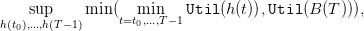sup min ( min Util (h (t)),Util (B (T ))), h(t0),...,h(T−1) t=t0,...,T− 1
(25)

under the contraints

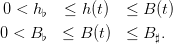
0 < h♭ ≤ h(t) ≤ B (t) 0 < B♭ ≤ B(t) ≤ B ♯.

The dynamic programming equation is:

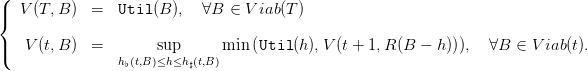( |{ V (T, B) = Util (B ), ∀B ∈ V iab(T) |( V (t,B) = sup min (Util (h),V (t + 1,R (B − h ))), ∀B ∈ V iab(t). h♭(t,B)≤h≤h♯(t,B)
(26)

Question 11 Adapt the result and the associated scilab code to compute maximin viable paths (B⋆(t),h⋆(t)).

3 Uncertain growth

The R(t) vary in an interval [R♭,R♯].

3.1 Worst intertemporal utility maximization

The maximization problem is

T−1 sup inf (∑ ρtUtil (h(t)) + ρT Util (B (T ))). h(t0),...,h(T−1)R(⋅)∈[R ♭,R♯]T+1 t=t0
(27)

Analytic resolution by dynamic programming

The dynamic programming equation is:

( |{ V (T,B ) = ρTUtil (B ), |( V (t,B ) = sup inf (ρtUtil (h) + V (t + 1,R (B − h))). 0≤h ≤BR ∈[R♭,R♯]
(28)

We restrict the study to the isoelastic case (4).

Question 12 Show that, as for the corresponding deterministic case in subsection 2.2, (6)–(11) hold true with R replaced by R♭.

scilab simulations

Question 13 Generate trajectories with robust optimal decision rule. Adapt the code in subsection 2.2 to draw trajectories. Compare the criterion values given by the random effort strategy, by your test strategy in Question 1, and by the optimal strategy.

3.2 Worst minimal utility maximization

The maximization problem is

sup inf min( min Util (h(t)),Util(B (T))). h(t0),...,h(T−1)R(⋅)∈[R♭,R♯]T+1 t=t0,...,T−1
(29)

Analytic resolution by dynamic programming

The dynamic programming equation is:

(| V (T,B ) = Util (B ) { |( V(t,B ) = 0s≤uhp≤B R∈[inRf♭,R ♯]min (Util (h),V (t + 1,R (B − h ))).
(30)

Question 14 Show that, as for the corresponding deterministic case in subsection 2.3, (16)–(17) hold true with R replaced by R♭.

scilab simulations

Question 15 Generate trajectories with robust viable decision rules. Adapt the code in subsection 2.3 to draw trajectories. Compare the criterion values given by the random effort strategy, by your test strategy in Question 1, and by the optimal strategy.

3.3 Tolerable window and guaranteed harvesting (robust viability)

We assume that the policy is to constrain the biomass level within an ecological window, namely between conservation and maximal safety values, whatever the scenario:

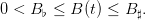0 < B♭ ≤ B (t) ≤ B♯.
(31)

A minimal catch is also required:

0 < h♭ ≤ h(t).
(32)

The dynamic programming equation for the robust viability kernels is:

( { Viab1(T ) = [B♭,B ♯], ( V iab (t) = {B ∈ [B ,B ] | ∃h ∈ [h ,B ],∀R ∈ [R ,R ],R (B − h ) ∈ V iab (t + 1)}. 1 ♭ ♯ ♭ ♭ ♯ 1
(33)

Question 16 Define by backward induction

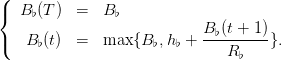
( { B♭(T ) = B ♭ B♭(t +-1) ( B ♭(t) = max {B ♭,h♭ + R ♭ }.

Show that, whenever

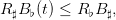
R♯B ♭(t) ≤ R ♭B♯,

the viability kernels are intervals:

V iab(t) = [B ♭(t),B ♯].

Show that the viable decision rules Catch(t,B) are those which belong to

[h♭(t,B),h ♯(t,B )] := [B − B-♯,B − B-♭(t +-1)]. R ♯ R ♭

References

[1]   M. Kot. Elements of Mathematical Ecology. Cambridge University Press, Cambridge, 2001.