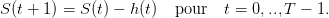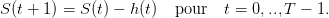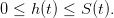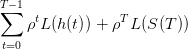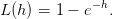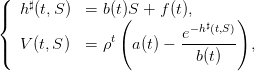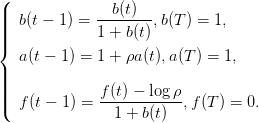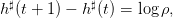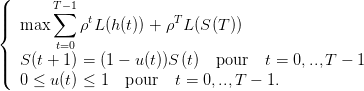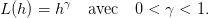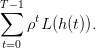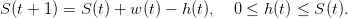Gestion optimale d’une ressource épuisable
Les questions

Michel de Lara
(last modification date: October 10, 2017)
Version pdf de ce document
Version sans bandeaux

1 Présentation du problème
2 Cas déterministe : utilité de type exponentiel
3 Cas déterministe : utilité de type puissance
4 Cas aléatoire

Contents

1 Présentation du problème
2 Cas déterministe : utilité de type exponentiel
 2.1 Résolution analytique par programmation dynamique
 2.2 Programmation sous Scilab
 2.3 Résolution par dynoptim, routine d’optimisation dynamique
3 Cas déterministe : utilité de type puissance
 3.1 Résolution analytique par programmation dynamique
 3.2 Résolution numérique par programmation dynamique
4 Cas aléatoire
 4.1 Modèle aléatoire
 4.2 Résolution numérique par programmation dynamique

1 Présentation du problème

On considère un planificateur souhaitant utiliser de manière optimale une ressource non renouvelable (pétrole, minerai, etc.) sur T périodes. Le niveau de la ressource à l’instant t est le stock S(t) et son prélèvement sur la période [t,t + 1[ est noté h(t), ce qui donne la dynamique suivante :

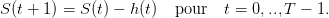S (t + 1) = S (t) − h(t) pour t = 0,..,T − 1.
(1)

On a

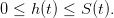0 ≤ h(t) ≤ S(t).
(2)

Le bien-être que le planificateur souhaite optimiser est représenté par la somme actualisée des utilités de ses prélèvements successifs h(t) (supposés liés à la consommation par exemple) et du stock final S(T)

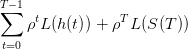T∑−1 t T ρ L (h(t)) + ρ L (S(T )) t=0
(3)

où ρ ∈ [0, 1] est un facteur d’actualisation et L(.) une fonction d’utilité.

2 Cas déterministe : utilité de type exponentiel

On suppose que l’utilité est de type exponentiel

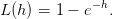L(h ) = 1 − e− h.
(4)

2.1 Résolution analytique par programmation dynamique

Question 1

  1. Que vaut la fonction valeur à l’instant final V (T,S) ?
  2. Quelle est la relation de récurrence liant les fonctions valeurs V (t − 1,.) et V (t,.)?
  3. Montrer que, pour certaines valeurs de t et de S, le prélèvement optimal en boucle fermée h♯(t,S) et la fonction valeur V (t,S) vérifient
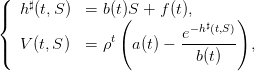    ( h♯(t,S ) = b(t)S + f(t), |{ ( ♯ ) t e−h-(t,S)- |( V (t,S ) = ρ a(t) − b(t) ,
    		(5)

    où les paramètres a(t),b(t),f(t) sont définis par les récurrences

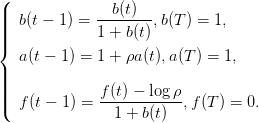    ( ||| b(t − 1) = --b(t)--,b(T) = 1, |||{ 1 + b(t) a(t − 1) = 1 + ρa(t),a(T ) = 1, | |||| f(t) − log ρ |( f(t − 1) = -----------,f(T ) = 0. 1 + b(t)
    		(6)

    En déduire alors que les prélèvements optimaux en boucle fermée h♯(t) = h♯(t,S♯(t)) où S♯(t + 1) = S♯(t) − h♯(t), satisfont la relation

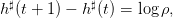    h♯(t + 1) − h ♯(t) = logρ,
    		(7)

    et qu’ils sont donc décroissants dans le temps.

2.2 Programmation sous Scilab

Question 2 Ouvrir un fichier nom_de_fichier.sce (par exemple, TP_renouv.sce) et y recopier les paramètres suivants.

Y construire les vecteurs b et f donnés par l’équation (6), puis créer les vecteurs de stocks et de prélèvements optimaux Sopt et hopt en utilisant la dynamique  (1) et l’équation (5) du feedback.

Tracer trajectoire et décisions optimales en fonction du temps, à l’aide de la commande Scilab plot2d2.

  //paramètres
  
  Horizon=4;
  //Horizon=40;
  S0=10;
  rho=0.8;
  
  // Construction de b et f
  
  b=[];
  b(Horizon+1)=1;
  for t=Horizon:-1:1 do
    b(t)=b(t+1)/(1+b(t+1));
  end;
  
  f=[];
  f(Horizon+1)=0;
  for t=Horizon:-1:1 do
    f(t)=(f(t+1)-log(rho))/(1+b(t+1));
  end;
  
  
  // Prélèvements  et ressource optimales
  
  Sopt=[];
  hopt=[];
  Sopt(1)=S0;
  for t=1:Horizon do
    hopt(t)=b(t)*Sopt(t)+f(t);
    Sopt(t+1)=(Sopt(t)-hopt(t));
  end,
  
  //vérification...
  //Sopt-[hopt ; Sopt($)]
  
  // Affichage
  xbasc();
  plot2d2([0:(Horizon+1);0:(Horizon+1)]',[[hopt;Sopt($);0]';[Sopt;0]']', ...
          rect = [0,0,Horizon+2,Sopt(1)+1])

Question 3 Répéter l’opération précédente pour différentes valeurs de l’horizon T. Commenter.

2.3 Résolution par dynoptim, routine d’optimisation dynamique

On introduit, pour des facilités de programmation, une nouvelle commande u ∈ [0, 1] telle que h = uS. On considère alors le problème

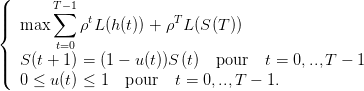( T∑− 1 |||{ max ρtL(h(t)) + ρTL (S (T)) | t=0 ||( S(t + 1) = (1 − u (t))S (t) pour t = 0,..,T − 1 0 ≤ u(t) ≤ 1 pour t = 0,..,T − 1.
(8)

comme un problème d’optimisation en la variable (S(0),...,S(T),u(0),...,u(T − 1)) ∈ ℝT+1 × [0, 1]T sous les contraintes d’égalité S(t + 1) = (1 − u(t))S(t) et d’inégalité 0 ≤ u(t) ≤ 1.

La macro dynoptim permet de traiter ce type de problèmes.

Question 4 Charger dynoptim (menu toolboxes sous Scilab) et consulter le help. Définir la dynamique dyn et ses dérivées partielles dyn_S par rapport à l’état S et dyn_u par rapport à la commande u. Faire de même avec le coût instantané et le coût final. Écrire les contraintes sur les commandes.

  //exec("/home/s/scilab-contrib/dynoptim-1.2/loader.sce");
  //exec /usr/local/scilab-cvs/contrib/dynoptim/loader.sce
  help dynoptim
  
  ////////////////////////
  //dynamique
  ////////////////////////
  
  function z=dyn(u,S,t) z=S*(1-u),endfunction;
  function D=dyn_S(u,S,t) D=1-u,endfunction;
  function D=dyn_u(u,S,t) D=-S,endfunction;
  
  ////////////////////////
  // Fonction d'utilité
  ////////////////////////
  
  function z=Utilite(h) z=1-exp(-h),endfunction;
  function D=DUtilite(h) D=exp(-h),endfunction;
  
  ////////////////////////
  // cout instantané (à minimiser !)
  ////////////////////////
  
  function z=L(u,S,t) z=-(rho^t)*Utilite(u*S),endfunction;
  function D=L_S(u,S,t) D=-(rho^t)*DUtilite(u*S)*u,endfunction;
  function D=L_u(u,S,t) D=-(rho^t)*DUtilite(u*S)*S,endfunction;
  
  ////////////////////////
  // cout final (à minimiser !)
  ////////////////////////
  
  function z=g(S,t) z=-(rho^t)*Utilite(S),endfunction;
  function D=g_S(S,t) D=-(rho^t)*DUtilite(S),endfunction;
  
  ////////////////////////
  // contrainte controles
  ////////////////////////
  
  u_min=zeros(1,Horizon);
  u_max=ones(1,Horizon);

Question 5 Choisir un niveau initial de ressource S0 et un horizon T. Initialiser l’algorithme d’optimisation dynamique dynoptim avec un vecteur u_init. Faire un appel à dynoptim et tracer les solutions. Vérifier dans quels cas les solutions coïncident avec celles des questions précédentes.

  Horizon=4;
  //Horizon=40;
  
  //conditions initiales
  S0=[10];
  u_init=0.5*ones(1,Horizon);
  
  ////////////////////
  // Appel dynoptimsc
  //////////////////////
  L_noms=["L","L_u","L_S"];
  dyn_noms=["dyn","dyn_u","dyn_S"];
  g_noms=["g","g_S"];
  
  [u_opt,S_opt]=dynoptim(L_noms,dyn_noms,g_noms,u_min,u_init,u_max,S0),
  
  h_opt=u_opt .*S_opt(1:($-1));
  
  // Affichage
  xbasc();
  plot2d2([0:(Horizon+1);0:(Horizon+1)]',[[h_opt';S_opt($);0]';[S_opt';0]']', ...
          rect = [0,0,Horizon+2,S_opt(1)+1])

Question 6 Que constatez-vous en faisant varier le facteur d’actualisation ρ ?

3 Cas déterministe : utilité de type puissance

On suppose que l’utilité est de type dit isoélastique :

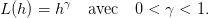L (h) = hγ avec 0 < γ < 1.
(9)

On suppose aussi que le bien-être que le planificateur souhaite optimiser est représenté par la somme actualisée des utilités de ses prélèvements successifs h(t)

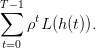T∑−1 t ρ L(h(t)). t=0
(10)

3.1 Résolution analytique par programmation dynamique

Question 7

  1. Montrer que l’équation de Bellman s’écrit, pour t = 0,...,T − 1,
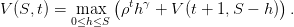    ( t γ ) V (S,t) = m0a≤xh≤S ρh + V(t + 1,S − h) .
    		(11)

  2. Montrer, par récurrence, que le prélèvement optimal h♯(t,S) et la fonction valeur V (t,S) satisfont
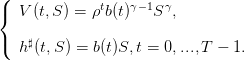    ( t γ−1 γ { V(t,S ) = ρ b(t) S , ( h♯(t,S ) = b(t)S,t = 0,...,T − 1.
    		(12)

    Montrer que l’équation de récurrence satisfaite par b(t) est

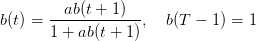    ab (t + 1) b(t) = -------------, b(T − 1) = 1 1 + ab(t + 1)
    		(13)

    où

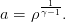    -1- a = ργ−1.
    		(14)

3.2 Résolution numérique par programmation dynamique

On restreint le modèle (1) aux états et aux commandes entiers : S(t) ∈ ℕ, h(t) ∈ ℕ.

On recopiera dans un fichier nom_de_fichier.sci (par exemple, TP_renouv.sci) la macro Bell_stoch suivante qui résoud numériquement l’équation de la programmation dynamique pour un problème de minimisation et non pas de maximisation comme ici. On la chargera sous Scilab par l’instruction exec(’TP_renouv.sci’).

  function [valeur,feedback]=Bell_stoch(matrice_transition,cout_instantane,cout_final)
    // MINIMISATION
    // algorithme de programmation dynamique stochastique
    //     pour une chaîne de Markov sur \{1,2...,cardinal_etat\}
    // matrice_transition = liste à cardinal_commande éléments
    //     composée de matrices de dimension (cardinal_etat,cardinal_etat)
    // cout_instantane = liste à cardinal_commande éléments
    //     composée de matrices de dimension (cardinal_etat,horizon-1)
    // cout_final = vecteur de dimension (1,cardinal_etat)
    // valeur = fonction valeur de Bellman,
    //     matrice de dimension (cardinal_etat,horizon)
    // feedback = commande en feedback sur l'état et le temps
    //     matrice de dimension (cardinal_etat,horizon-1)
  
    ee=size(cout_instantane(1));cardinal_etat=ee(1);
    cardinal_commande=size(cout_instantane);
    hh=size(cout_instantane(1));horizon=1+hh(2);
  
    valeur=0*ones(cardinal_etat,horizon);
    // tableau ou l'on stocke la fonction de Bellman
    // valeur(:,t) est un vecteur
    // : représente ici le vecteur d'état
  
    valeur(:,horizon)=cout_final;
    // La fonction valeur au temps T est cout_final
  
    feedback=0*ones(cardinal_etat,horizon-1);
    // tableau ou l'on stocke le feedback u(x,t)
  
    // Calcul rétrograde de la fonction de Bellman et
    // de la commande optimale à la date 'temp' par l'équation de Bellman
    // On calcule le coût pour la commande choisie connaissant la valeur de la
    // fonction coût à la date suivante pour l'état obtenu
  
    for temp=horizon:-1:2 do
      // équation rétrograde
      // (attention, pour des questions d'indices, bien finir en :2)
      loc=zeros(cardinal_etat,cardinal_commande);
      // variable locale contenant les valeurs de la fonction valeur de Bellman
      // loc est une matrice
      for j=1:cardinal_commande do
        loc(:,j)=matrice_transition(j)*valeur(:,temp)+cout_instantane(j)(:,temp-1);
      end;
  
      [mm,jj]=mini(loc,'c')
      // mm est le minimum atteint
      // jj est la commande qui réalise le minimum
  
      valeur(:,temp-1)=mm;
      // coût optimal
      feedback(:,temp-1)=jj;
      // feedback optimal
    end
  endfunction

On recopiera également dans le même fichier la macro trajopt suivante qui calcule des trajectoires optimales.

  function z=trajopt(matrice_transition,feedback,cout_instantane,cout_final,etat_initial)
    // z est une liste :
    // z(1) est la trajectoire optimale obtenue partant de etat_initial
    // z(2) est la trajectoire correspondante des commandes optimales
    // z(3) est la trajectoire correspondante des coûts
    // etat_initial = un entier
    // pour le reste, voir la macro Bell_stoch
  
    ee=size(cout_instantane(1));cardinal_etat=ee(1);
    cardinal_commande=size(cout_instantane);
    hh=size(cout_instantane(1));horizon=1+hh(2);
  
    z=list();
    x=etat_initial;
    u=[];
    c=[];
  
    for j=1:horizon-1 do
      u=[u,feedback(x($),j)];
      c=[c,c($)+cout_instantane(u($))(x($),j)];
      mat_trans=full(matrice_transition(u($)));
      x=[x,grand(1,'markov',mat_trans,x($))];
    end
    c=[c,c($)+cout_final(x($))];
  
    z(1)=x;z(2)=u;z(3)=c;
  endfunction

Question 8 Choisir des valeurs pour le stock initial, l’horizon, l’exposant de la fonction d’utilité. Saisir la dynamique du système par le biais d’une matrice de transition, et saisir les coûts instantané et final. Tracer différentes trajectoires optimales.

  exec('TP_renouv.sci')
  
  stacksize(10000000);
  
  S0=100;
  stock=0:S0;
  commande=0:S0;
  
  T=30;
  puis=0.5;
  rho=0.99;
  
  
  function y=cutoff(x,a)
    y=min(x,a)-a .*bool2s(x > a);
  endfunction
  
  
  cout_inst=list()
  for l=1:(S0+1) do
    // i.e. h=0,...,S0
    cout_inst(l)=-(cutoff(l-1,(1:(S0+1))'-1))^puis*rho^(1:T);
    // si h=l-1 > S, le coût est nul
    // sinon h^puis
  end;
  
  cout_fin=zeros(1,S0+1)';
  
  mat_trans=list()
  for l=1:(S0+1) do
    mat_trans(l)=zeros(S0+1,S0+1);
    // etats = stocks de 0 à S0
    for i=1:(S0+1) do
      mat_trans(l)(i,max(1,i-l+1))=1;
      // si h=l-1 > S, le coût est nul
    end;
  end;
  
  [valeur,feedback]=Bell_stoch(mat_trans,cout_inst,cout_fin);
  
  etat_initial=S0+1;
  
  zz=trajopt(mat_trans,feedback,cout_inst,cout_fin,etat_initial);
  // calcul des trajectoires optimales
  
  xset("window",1);xbasc();
  plot2d2(1:prod(size(zz(1))),stock(zz(1)),rect = [0,0,T,S0]);
  xtitle("stock")
  
  xset("window",2);xbasc();
  plot2d2(1:prod(size(zz(2))),commande(zz(2)),rect = [0,0,T,S0]);
  xtitle("commande")
  
  xset("window",3);xbasc();plot2d2(1:prod(size(zz(3))),-zz(3));xtitle("critère")
  // tracé des trajectoires optimales

4 Cas aléatoire

4.1 Modèle aléatoire

On suppose que de nouvelles ressources w(t) (éventuellement nulles) sont découvertes dans la période [t,t + 1[, donnant

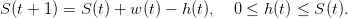S(t + 1) = S(t) + w(t) − h(t), 0 ≤ h(t) ≤ S(t).
(15)

On suppose que w(0),...,w(T − 1) sont des variables aléatoires entières indépendantes et de même loi.

4.2 Résolution numérique par programmation dynamique

Question 9 Préciser les hypothèses mathématiques sous-jacentes au code Scilab suivant. Tracer différentes trajectoires optimales.

  aleas=[0,10];
  //probas=ones(aleas)/sum(ones(aleas));
  probas=[0.9,0.1];
  
  mat_trans=list()
  for l=1:(S0+1) do
    mat_trans(l)=zeros(S0+1,S0+1);
    // etats = stocks de 0 à S0
    for i=1:(S0+1) do
      for j=1:sum(ones(aleas)) do
        mat_trans(l)(i,min(max(1,i-l+aleas(j)),S0+1))=mat_trans(l)(i, ...
                                                                   min(max(1,i-l+aleas(j)), ...
                                                                       S0+1))+probas(j);
      end;
    end;
  end;
  
  // vérification
  verif=0;
  for l=1:(S0+1) do
    verif=verif+abs(sum(sum(mat_trans(l),'c')-1));
  end
  verif

  [valeur,feedback]=Bell_stoch(mat_trans,cout_inst,cout_fin);
  
  etat_initial=S0+1;
  
  zz=trajopt(mat_trans,feedback,cout_inst,cout_fin,etat_initial);
  // calcul des trajectoires optimales
  
  
  xset("window",1);xbasc();
  plot2d2(1:prod(size(zz(1))),stock(zz(1)),rect = [0,0,T,S0]);
  xtitle("stock")
  
  xset("window",2);xbasc();
  plot2d2(1:prod(size(zz(2))),commande(zz(2)),rect = [0,0,T,S0]);
  xtitle("commande")
  
  xset("window",3);xbasc();plot2d2(1:prod(size(zz(3))),-zz(3));xtitle("critère")
  // tracé des trajectoires optimales