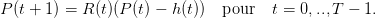
On considère un planificateur souhaitant utiliser de manière optimale une ressource naturelle renouvelable (forêt, poissons...) sur T périodes. Le niveau de la ressource à l’instant t est noté P(t) et son prélèvement sur la période [t,t + 1[ est noté h(t). On suppose que la ressource non extraite à l’instant t se renouvelle à un taux de croissance R(t), ce qui donne la dynamique suivante :
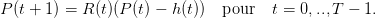 | (1) |
Le bien-être que le planificateur souhaite optimiser est représenté par la somme actualisée des utilités de ses prélèvements successifs h(t) (supposés liés à la consommation par exemple) et du niveau de la ressource finale P(t) :
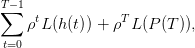
On suppose tout d’abord que la ressource naturelle est constituée d’une seule ressource de croissance certaine et constante R:
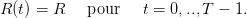 | (2) |
Le planificateur souhaite optimiser le bien-être soit
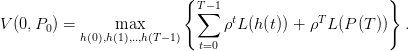 | (3) |
On suppose maintenant que l’utilité est de type exponentiel
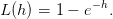 | (4) |
Question 1
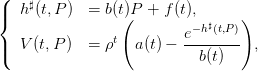 | (5) |
où les paramètres a(t),b(t),f(t) sont définis par les récurrences
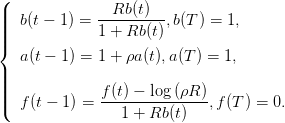 | (6) |
En déduire que les prélèvements optimaux en boucle fermée h(t) := h♯(t,P♯(t)) où P♯(t + 1) = R(P♯(t) − h♯(t,P♯(t))) satisfont la relation :
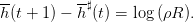 | (7) |
Donner alors des conditions sur ρ et R pour que les prélèvements optimaux soient croissants dans le temps. Que se passe-t-il en particulier si ρR = 1 ?
Question 2 Ouvrir un fichier nom_de_fichier.sce (par exemple, TP_renouv.sce) et y recopier les paramètres suivants.
Y construire les vecteurs b et f donnés par l’équation (6), puis créer les vecteurs de stocks et de prélèvements optimaux Popt et hopt en utilisant la dynamique (1) et l’équation (5) du feedback.
Tracer trajectoire et décisions optimales en fonction du temps, à l’aide de la commande Scilab plot2d2. On notera que le vecteur hopt est de taille (1,T), alors que Popt est de taille (1,T + 1) ; on rajoutera donc la dernière valeur Popt($) de Popt à hopt pour signifier que le dernier prélèvement consiste à épuiser totalement la ressource.
Question 3 Répéter l’opération précédente pour différentes valeurs du taux d’actualisation ρ entre 0.5 et 1. Quel résultat analytique retrouve-t-on ?
On introduit, pour des facilités de programmation, une nouvelle commande u ∈ [0, 1] telle que h = uP. On considère alors le problème
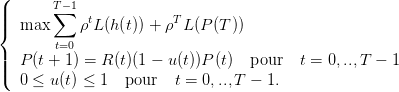 | (8) |
comme un problème d’optimisation en la variable (P(0),...,P(T),u(0),...,u(T − 1)) ∈ ℝT+1 × [0, 1]T sous les contraintes d’égalité P(t + 1) = R(t)(1 − u(t))P(t) et d’inégalité 0 ≤ u(t) ≤ 1.
La macro dynoptim permet de traiter ce type de problèmes.
Question 4 Charger dynoptim (menu toolboxes sous Scilab) et consulter le help. Définir la dynamique dyn et ses dérivées partielles dyn_P par rapport à l’état et dyn_u par rapport à la commande. Faire de même avec le coût instantané et le coût final. Écrire les contraintes sur les commandes.
Question 5 Choisir un niveau initial de ressource S0 et un horizon T. Initialiser l’algorithme d’optimisation dynamique dynoptim avec un vecteur u_init. Faire un appel à dynoptim et tracer les solutions. Vérifier dans quels cas les solutions coïncident avec celles des questions précédentes.
Question 6 Que constatez-vous en faisant varier le facteur d’actualisation ρ ?
On suppose maintenant que la ressource totale P(t) est constituée de deux ressources P1(t) et P2(t). Le taux de croissance de la première ressource, supposé aléatoire, est notée M(t), tandis que la seconde ressource a une croissance certaine, de taux noté N. On appelle α(t) la proportion de la ressource P2 dans le total des ressources P(t) à la période t. Ainsi, le taux de croissance total, aussi aléatoire, s’écrit:
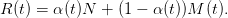 | (9) |
Pour simplifier, on suppose que les variables aléatoires (M(t))t=0,...,T−1 sont indépendantes et de même loi.
On considère aussi le niveau de prélèvement agrégé h(t) comme décision, ce qui donne la dynamique
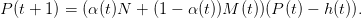 | (10) |
On suppose que le planificateur optimise l’espérance de la somme actualisée des utilités de ses prélèvements successifs et de la ressource finale
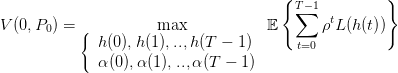 | (11) |
où h(t) et α(t) correspondent à une stratégie de prélèvement et de répartition.
On se restreint ici au cas dit isoélastique correspondant à une utilité
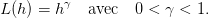 | (12) |
Question 7
![( )
V (P,t) = max ρtL(h ) + 𝔼 (V(t + 1,(αN + (1 − α)M )(P − h)) ,
α∈[0,1],h≥0](Ressource_renouvelable_Q13x.png) | (13) |
où M est une variable aléatoire de même loi que la loi commune des (M(t)).
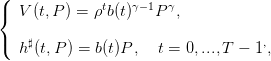 | (14) |
et
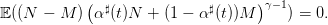 | (15) |
Montrer que l’équation de récurrence satisfaite par b(t) est
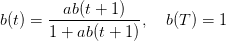 | (16) |
où on utilise 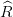 , l’équivalent certain de croissance optimale, c’est-à-dire
, l’équivalent certain de croissance optimale, c’est-à-dire
![L(^R ) = 𝔼[L(R ♯)] avec R ♯ = α♯N + (1 − α♯)M](Ressource_renouvelable_Q18x.png) | (17) |
et le terme
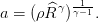 | (18) |
On suppose que
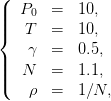
Question 8 Ouvrir un fichier nom_de_fichier.sce et y recopier les paramètres précédents. Écrire une fonction scilab util(x) pour la fonction d’utilité puissance.
On suppose aussi que le taux de croissance risqué M suit une loi du type
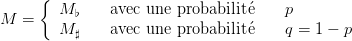 | (19) |
Question 9 Montrer que la solution de (15) est donnée par
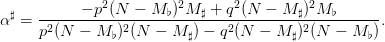 | (20) |
Prendre les paramètres suivants pour p,q,M♭,M♯. Calculer la proportion optimale α♯ de la ressource 1.
Question 11 Écrire une fonction Scilab qui, à un niveau global de ressource ressource P et à une valeur M de taux de croissance, associe le niveau total de la ressource au pas de temps suivant résultant de l’application de la commande optimale (h♯(t,P),α♯).
Question 12 Écrire une procédure de simulation de la variable aléatoire M.
Question 13 À partir de P0, générer une trajectoire optimale stochastique P♯(t) de
ressources. Tracer les trajectoires t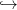 (P♯(t),h♯(t)) pour une réalisation de M.
(P♯(t),h♯(t)) pour une réalisation de M.
Question 14 Écrire une procédure Scilab fournissant S réalisations des variables aléatoires J(h♯(.)), P♯(t) et h♯(t). En déduire des valeurs approchées pour leur moyenne et variance. Donner un histogramme de J(h♯(.)).