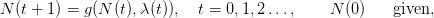
We describe the dynamics of the exploited resource by a controlled dynamic system in discrete time, where the time step is one year. At each time t ∈ ℕ, let us consider Na(t) the abundance of the stock at age a ∈{1,…,A} and λ(t) the fishing mortality multiplier (control), supposed to be taken at the beginning of period [t,t + 1[. Introducing the state vector N(t) = (N1(t),…,Na(t)) (in short: stock), belonging to the state space ℝ+A (ℝ + the set of nonnegative real numbers), the following dynamic system is considered
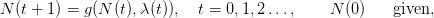 | (1) |
where the vector function g = 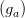 a=1,…,A is defined for any N ∈ ℝ+A and λ ∈ ℝ
+ by
a=1,…,A is defined for any N ∈ ℝ+A and λ ∈ ℝ
+ by
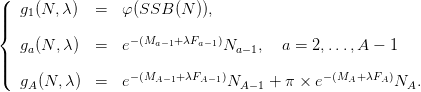 | (2) |
The function φ describes a stock recruitment (S-R) relationship. The spawning stock biomass SSB is defined by
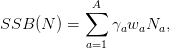 | (3) |
with γa the proportion of mature individuals at age and wa the weight at age. The parameter π ∈{0, 1} is related to the existence of a plus-group to describe the population dynamics for ages greater than A. If we neglect the survivors after age A then π = 0, else π = 1 and the last age class is a plus group.
Here is the data for the Bay of Biscay anchovy. Write the following lines in a file viab_fish.sce.
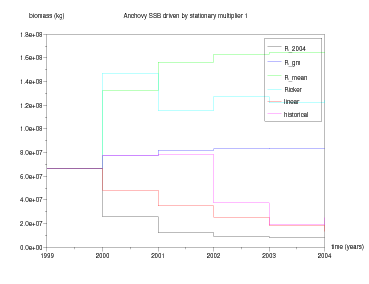
Question 1 Draw trajectories for different stock-recruitment relationships with same initial condition and fishing mortality multiplier equal to 1.
Write the following lines in a file viab_fish.sci.
Add the following lines in the file viab_fish.sce, then execute this latter.
Two indicators are used in the precautionary approach, with associated limit reference points. The first indicator, denoted by SSB in (3), is the spawning stock biomass, to which we associate the reference point Blim > 0. For management advice an additional precautionary reference point Bpa > Blim is used, intended to incorporate uncertainty about stock state.
The second indicator, denoted by F, is the mean fishing mortality over a pre-determined age range from ar to Ar, that is
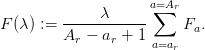 | (4) |
Associated limit reference point is Flim and a precautionary approach reference point Fpa > 0. Acceptable controls λ, according to this reference point, are those for which F(λ) ≤ Flim, as higher F rates might drive SSB below its limit reference point.
To define sustainability, we now assume that the decision maker can describe “acceptable configurations of the system”, that is acceptable couples (N,λ) of states and controls, which form a set 𝔻 ⊂ ℝ+A × ℝ +, the acceptable set. In practice, the set 𝔻 may capture ecological, economic and/or sociological requirements.
Considering sustainable management within the precautionary approach, involving SSB and F indicators, we introduce the following precautionary approach configuration set
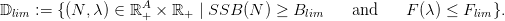 | (5) |
A subset 𝕍 ⊂ ℝ+A of the state space ℝ +A is said to be a viability domain for dynamics g in the acceptable set 𝔻 if
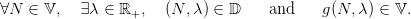 | (6) |
In other words, if one starts from a stock in 𝕍, there exists an appropriate fishing mortality multiplier such that the system is in an acceptable configuration and the next time step state is also in 𝕍. For example, acceptable equilibria ((N,λ) ∈ 𝔻 and g(N,λ) = N) are viability domains.
Given a viability domain 𝕍, the viable controls associated with any state N ∈ 𝕍 are those controls which let state within the viability domain at next time step, that is which belong to the following (non empty) set
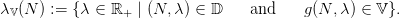 | (7) |
Let us define the precautionary approach state set
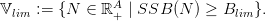 | (8) |
We shall say that the precautionary approach is sustainable if the precautionary approach state set 𝕍lim given by (8) is a viability domain for dynamics g in the acceptable set 𝔻lim.
In [1], we prove the following result.
Result 1 If we suppose that the natural mortality is independent of age, that is Ma = M, and that the proportion γa of mature individuals and the weight wa at age are increasing with age a, the precautionary approach is sustainable if and only if
![[ ]
inf πe −M x + γ1w1 φ(x) ≥ Blim.
x∈[Blim,+∞ [](SSB_fish_management10x.png) | (9) |
that is, if and only if the lowest possible sum of survivors (weighted by growth and maturation) and newly recruited spawning biomass is above Blim.
A constant recruitment is generally used for fishing advice, so the following simplified condition can be used.
Result 2 Assuming a constant recruitment R, the precautionary approach is sustainable if and only if we have πe−MB lim + γ1w1R ≥ Blim, that is if and only if
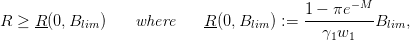 | (10) |
making thus of R(0,Blim) a minimum recruitment required to preserve Blim.
Question 2 Compute R(0,Blim). Compare with the different constant recruitment values. Comment.
The precautionary approach can be sketched as follows: an estimate of the stock vector N is made; the condition SSB(N) ≥ Blim is checked; if valid, the following usual advice is given
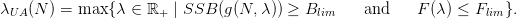 | (11) |
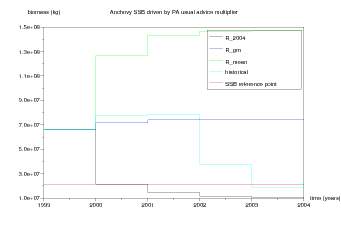
Question 3 Starting from 1999, simulate the effect of the usual advice strategy λUA in (11) on dynamics differing by their constant recruitment. Comment the trajectories.
Question 4 Propose the largest Blim such that the precautionary approach is sustainable with every observed constant recrutment. Illustrate the result with simulations.